目录
3:word2vec
a 推导关于词向量的梯度
在以softmax为假设函数的word2vec中:
$$\begin{align}
\hat{\boldsymbol{y}}_{o} &= p(\boldsymbol{o} \vert \boldsymbol{c}) =
\frac{exp(\boldsymbol{u}_{0}^{T} \boldsymbol{v}_{c})}{\sum\limits_{w=1}^{W} exp(\boldsymbol{u}_{w}^{T} \boldsymbol{v}_{c})}
\end{align}$$
$\boldsymbol{v}_{c}$是中央单词的词向量,$\boldsymbol{w}$ 是第 $w$个词语, $\boldsymbol{u}_{w}$ ($w = 1,…,W$) 是词表中所有单词的输出词向量。假设使用交叉熵作为损失函数, $\boldsymbol{o}$ 为正确单词 (one-hot向量的第 $\boldsymbol{o}$维为1),请推导损失函数关于$\boldsymbol{v}_c$的梯度。
一些有用的记号:
$$\begin{align}
J_{softmax-CE}(\boldsymbol{o}, \boldsymbol{v}_{c}, \boldsymbol{U}) &= CE(\boldsymbol{y}, \hat{\boldsymbol{y}})
\end{align}$$
其中$\boldsymbol{U}$ = $[\boldsymbol{u}_{1}$,$\boldsymbol{u}_{1}$,$\dots$, $\boldsymbol{u}_{W}]$是所有词向量构成的矩阵。
解答:
由于 $\frac{\partial J}{\partial \boldsymbol{z}} = (\hat{\boldsymbol{y}} – \boldsymbol{y})$ 是词表大小的“概率列向量”,而 $\boldsymbol{U}$ 是 $D\times W$ 的矩阵($\boldsymbol{U} = [\boldsymbol{u}_{1}$,$\boldsymbol{u}_{1}$,$\dots$, $\boldsymbol{u}_{W}]$),$z=U^T \cdot v_c$,根据链式法则需要乘上$\boldsymbol{U}^{T}$的转置,即:
$$\begin{align}
\frac{\partial J}{\partial \boldsymbol{v_c}} &= %
\boldsymbol{U} (\hat{\boldsymbol{y}} - \boldsymbol{y}) \nonumber
\end{align}$$
b 推导关于lookup-table的梯度
与上题同理:
$$\begin{align}
\frac{\partial J}{\partial \boldsymbol{U}} &= %
\boldsymbol{v}_{c} (\hat{\boldsymbol{y}} - \boldsymbol{y})^{T} \nonumber
\end{align}$$
c 负采样时的梯度推导
假设进行负采样,样本数为$\boldsymbol{K}$,正确答案为$\boldsymbol{o}$,那么有$o \notin \{1,...,K\}$。负采样损失函数定义如下:
$$\begin{align}
J_{neg-sample}(\boldsymbol{o}, \boldsymbol{v}_{c}, \boldsymbol{U}) &= %
− log(\sigma(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c})) - \sum\limits_{k=1}^{K} log(\sigma(-\boldsymbol{u}_{k}^{T} \boldsymbol{v}_{c}))
\end{align}$$
其中,
$$\begin{align} \sigma(x) &= \frac{1}{1 + e^{-x}} \nonumber \\ &= \frac{e^{x}}{1 + e^{x}} \nonumber \\ \frac{\partial}{\partial x} \sigma(x) &= \sigma(x) \times (1 - \sigma(x)) \nonumber \\ \end{align}$$
先对$v_c$求导吧,然后当成微分方程得到$u_o$或$u_k$的导数:
$$\begin{align}
\frac{\partial J}{\partial v_c}&=\left(\sigma(u_o^Tv_c)-1\right)u_o-\sum_{k=1}^K\left(\sigma(-u_k^Tv_c)-1\right)u_k\\
\frac{\partial J}{\partial u_o}&=\left(\sigma(u_o^Tv_c)-1\right)v_c\\
\frac{\partial J}{\partial u_k}&=-\left(\sigma(-u_k^Tv_c)-1\right)v_c\\
\end{align}$$
这个损失函数比交叉熵要快,因为仅仅计算负样本和答案的梯度$[w_{o}, w_{k},\dots,w_{K}]$,而不是 $\forall w_{j} \in W$。
d 全部梯度
推导窗口半径$m$的上下文[word$_{c−m}$ ,...,word$_{c−1}$ ,word$_{c}$ ,word$_{c+1}$ ,...,word$_{c+m}$ ]时,skip-gram 和 CBOW的损失函数$F(\boldsymbol{o}, \boldsymbol{v}_{c})$ ($\boldsymbol{o}$ 是正确答案的词向量)或说$J_{softmax-CE}(\boldsymbol{o},\boldsymbol{v}_{c},\dots)$ 或 $J_{neg-sample}(\boldsymbol{o},\boldsymbol{v}_{c},\dots)$ 关于每个词向量的梯度。
对于skip-gram来讲,$c$的上下文对应的损失函数是:
$$\begin{align}
J_{skip-gram}(word_{c-m \dots c+m}) &= %
\sum\limits_{-m \leq j \leq m, j \ne 0} F(\boldsymbol{w}_{c+j}, \boldsymbol{v}_{c})
\end{align}$$
这里 $\boldsymbol{w}_{c+j}$ 是离中心词距离$j$的那个单词。
而CBOW稍有不同,不使用中心词$\boldsymbol{v}_{c}$而使用上下文词向量的和 $\hat{\boldsymbol{v}}$ 作为输入去预测中心词:
$$\begin{align}
\hat{\boldsymbol{v}} &= \sum\limits_{-m \leq j \leq m, j \ne 0} \boldsymbol{v}_{c+j}
\end{align}$$
然后CBOW的损失函数是:
$$\begin{align}
J_{CBOW}(word_{c-m \dots c+m}) &= F(\boldsymbol{w}_{c}, \hat{\boldsymbol{v}})
\end{align}$$
解答:
根据前面的推导,知道如何得到梯度$\begin{align} \frac{\partial J}{\partial \boldsymbol{v_c}} &= \boldsymbol{U}^{T} (\hat{\boldsymbol{y}} - \boldsymbol{y}) \nonumber \end{align}$和$\begin{align} \frac{\partial J}{\partial \boldsymbol{U}} &= \boldsymbol{v}_{c} (\hat{\boldsymbol{y}} - \boldsymbol{y})^{T} \nonumber \end{align}$。那么所求的梯度可以写作:
skip-gram
$$\begin{align}
\frac{J_{skip-gram}(word_{c-m \dots c+m})}{\partial \boldsymbol{U}} &= %
\sum\limits_{-m \leq j \leq m, j \ne 0} \frac{\partial F(\boldsymbol{w}_{c+j}, \boldsymbol{v}_{c})}{\partial \boldsymbol{U}} \nonumber \\
%
\frac{J_{skip-gram}(word_{c-m \dots c+m})}{\partial \boldsymbol{v}_{c}} &= %
\sum\limits_{-m \leq j \leq m, j \ne 0} \frac{\partial F(\boldsymbol{w}_{c+j}, \boldsymbol{v}_{c})}{\partial \boldsymbol{v}_{c}} \nonumber \\
%
\frac{J_{skip-gram}(word_{c-m \dots c+m})}{\partial \boldsymbol{v}_{j}} &= 0, \forall j\ne c \nonumber
\end{align}$$
CBOW
$$\begin{align}
\frac{J_{CBOW}(word_{c-m \dots c+m})}{\partial \boldsymbol{U}} &= %
\frac{\partial F(\boldsymbol{w}_{c}, \hat{\boldsymbol{v}})}{\partial \boldsymbol{U}} \nonumber \\
%
\frac{J_{CBOW}(word_{c-m \dots c+m})}{\partial \boldsymbol{v}_{j}} &= %
\frac{\partial F(\boldsymbol{w}_{c}, \hat{\boldsymbol{v}})}{\partial \hat{\boldsymbol{v}}}, \forall (j \ne c) \in \{c-m \dots c+m\} \nonumber \\
%
\frac{J_{CBOW}(word_{c-m \dots c+m})}{\partial \boldsymbol{v}_{j}} &= 0, %
\forall (j \ne c) \notin \{c-m \dots c+m\} \nonumber
\end{align}$$
e 实现SGD训练
将矩阵的每个行向量的长度归一化为1:
def normalizeRows(x): """ Row normalization function Implement a function that normalizes each row of a matrix to have unit length. """ ### YOUR CODE HERE denom = np.apply_along_axis(lambda x: np.sqrt(x.T.dot(x)), 1, x) x /= denom[:, None] ### END YOUR CODE return x
交叉熵损失与梯度:
def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
""" Softmax cost function for word2vec models
Implement the cost and gradients for one predicted word vector
and one target word vector as a building block for word2vec
models, assuming the softmax prediction function and cross
entropy loss.
Arguments:
predicted -- numpy ndarray, predicted word vector (\hat{v} in
the written component)
target -- integer, the index of the target word
outputVectors -- "output" vectors (as rows) for all tokens
dataset -- needed for negative sampling, unused here.
Return:
cost -- cross entropy cost for the softmax word prediction
gradPred -- the gradient with respect to the predicted word
vector
grad -- the gradient with respect to all the other word
vectors
We will not provide starter code for this function, but feel
free to reference the code you previously wrote for this
assignment!
"""
### YOUR CODE HERE
## Gradient for $\hat{\boldsymbol{v}}$:
# Calculate the predictions:
vhat = predicted
z = np.dot(outputVectors,vhat)
preds = softmax(z)
# Calculate the cost:
cost = -np.log(preds[target])
# Gradients
z = preds.copy()
z[target] -= 1.0
grad = np.outer(z, vhat)
gradPred = np.dot(outputVectors.T, z)
### END YOUR CODE
return cost, gradPred, grad
负采样与梯度:
def negSamplingCostAndGradient(predicted, target, outputVectors, dataset, K=10): """ Negative sampling cost function for word2vec models Implement the cost and gradients for one predicted word vector and one target word vector as a building block for word2vec models, using the negative sampling technique. K is the sample size. Note: See test_word2vec below for dataset's initialization. Arguments/Return Specifications: same as softmaxCostAndGradient """ # Sampling of indices is done for you. Do not modify this if you # wish to match the autograder and receive points! indices = [target] indices.extend(getNegativeSamples(target, dataset, K)) ### YOUR CODE HERE grad = np.zeros(outputVectors.shape) gradPred = np.zeros(predicted.shape) cost = 0 z = sigmoid(np.dot(outputVectors[target], predicted)) cost -= np.log(z) grad[target] += predicted * (z - 1.0) gradPred += outputVectors[target] * (z - 1.0) for k in xrange(K): samp = indices[k + 1] z = sigmoid(np.dot(outputVectors[samp], predicted)) cost -= np.log(1.0 - z) grad[samp] += predicted * z gradPred += outputVectors[samp] * z ### END YOUR CODE return cost, gradPred, grad
skipgram:
def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient=softmaxCostAndGradient): """ Skip-gram model in word2vec Implement the skip-gram model in this function. Arguments: currrentWord -- a string of the current center word C -- integer, context size contextWords -- list of no more than 2*C strings, the context words tokens -- a dictionary that maps words to their indices in the word vector list inputVectors -- "input" word vectors (as rows) for all tokens outputVectors -- "output" word vectors (as rows) for all tokens word2vecCostAndGradient -- the cost and gradient function for a prediction vector given the target word vectors, could be one of the two cost functions you implemented above. Return: cost -- the cost function value for the skip-gram model grad -- the gradient with respect to the word vectors """ cost = 0.0 gradIn = np.zeros(inputVectors.shape) gradOut = np.zeros(outputVectors.shape) ### YOUR CODE HERE cword_idx = tokens[currentWord] vhat = inputVectors[cword_idx] for j in contextWords: u_idx = tokens[j] c_cost, c_grad_in, c_grad_out = \ word2vecCostAndGradient(vhat, u_idx, outputVectors, dataset) cost += c_cost gradIn[cword_idx] += c_grad_in gradOut += c_grad_out ### END YOUR CODE return cost, gradIn, gradOut
f 实现SGD
mini-batch已经写好了,学习率递减也写好了,直接算梯度乘以学习率即可:
def sgd(f, x0, step, iterations, postprocessing=None, useSaved=False, PRINT_EVERY=10): """ Stochastic Gradient Descent Implement the stochastic gradient descent method in this function. Arguments: f -- the function to optimize, it should take a single argument and yield two outputs, a cost and the gradient with respect to the arguments x0 -- the initial point to start SGD from step -- the step size for SGD iterations -- total iterations to run SGD for postprocessing -- postprocessing function for the parameters if necessary. In the case of word2vec we will need to normalize the word vectors to have unit length. PRINT_EVERY -- specifies how many iterations to output loss Return: x -- the parameter value after SGD finishes """ # Anneal learning rate every several iterations ANNEAL_EVERY = 20000 if useSaved: start_iter, oldx, state = load_saved_params() if start_iter > 0: x0 = oldx step *= 0.5 ** (start_iter / ANNEAL_EVERY) if state: random.setstate(state) else: start_iter = 0 x = x0 if not postprocessing: postprocessing = lambda x: x expcost = None for iter in xrange(start_iter + 1, iterations + 1): # Don't forget to apply the postprocessing after every iteration! # You might want to print the progress every few iterations. cost = None ### YOUR CODE HERE cost, grad = f(x) x -= step * grad postprocessing(x) ### END YOUR CODE if iter % PRINT_EVERY == 0: if not expcost: expcost = cost else: expcost = .95 * expcost + .05 * cost print "iter %d: %f" % (iter, expcost) if iter % SAVE_PARAMS_EVERY == 0 and useSaved: save_params(iter, x) if iter % ANNEAL_EVERY == 0: step *= 0.5 return x
g 在斯坦福情感树库上训练词向量
只要运行q3_run.py就行了:
iter 40000: 9.587131 sanity check: cost at convergence should be around or below 10 training took 5090 seconds
得到:
h 附加题:实现CBOW
def cbow(currentWord, C, contextWords, tokens, inputVectors, outputVectors, dataset, word2vecCostAndGradient=softmaxCostAndGradient): """CBOW model in word2vec Implement the continuous bag-of-words model in this function. Arguments/Return specifications: same as the skip-gram model Extra credit: Implementing CBOW is optional, but the gradient derivations are not. If you decide not to implement CBOW, remove the NotImplementedError. """ cost = 0.0 gradIn = np.zeros(inputVectors.shape) gradOut = np.zeros(outputVectors.shape) ### YOUR CODE HERE predicted_indices = [tokens[word] for word in contextWords] predicted_vectors = inputVectors[predicted_indices] predicted = np.sum(predicted_vectors, axis=0) target = tokens[currentWord] cost, gradIn_predicted, gradOut = word2vecCostAndGradient(predicted, target, outputVectors, dataset) for i in predicted_indices: gradIn[i] += gradIn_predicted ### END YOUR CODE return cost, gradIn, gradOut
这里上下文向量是所有上下文词向量的和,却把梯度应用到了所有的上下文词向量上去。虽然看上去挺疯狂,但就是管用。
4 情感分析
在斯坦福情感树库做5个类别的情感分析,模型是简单的softmax,仅要求准确率至少$36.5\%$。
a 特征向量
一种最简单的特征选择方法就是取所有词向量的平均:
def getSentenceFeatures(tokens, wordVectors, sentence): """ Obtain the sentence feature for sentiment analysis by averaging its word vectors """ # Implement computation for the sentence features given a sentence. # Inputs: # tokens -- a dictionary that maps words to their indices in # the word vector list # wordVectors -- word vectors (each row) for all tokens # sentence -- a list of words in the sentence of interest # Output: # - sentVector: feature vector for the sentence sentVector = np.zeros((wordVectors.shape[1],)) ### YOUR CODE HERE for s in sentence: sentVector += wordVectors[tokens[s], :] sentVector *= 1.0 / len(sentence) ### END YOUR CODE assert sentVector.shape == (wordVectors.shape[1],) return sentVector
b 正则化的意义
避免过拟合,提高对未知实例的泛化能力。
c 调参
在验证集上搜索超参数:
def getRegularizationValues():
"""Try different regularizations
Return a sorted list of values to try.
"""
values = None # Assign a list of floats in the block below
### YOUR CODE HERE
values = np.logspace(-4, 2, num=100, base=10)
### END YOUR CODE
return sorted(values)
def chooseBestModel(results):
"""Choose the best model based on parameter tuning on the dev set
Arguments:
results -- A list of python dictionaries of the following format:
{
"reg": regularization,
"clf": classifier,
"train": trainAccuracy,
"dev": devAccuracy,
"test": testAccuracy
}
Returns:
Your chosen result dictionary.
"""
bestResult = None
### YOUR CODE HERE
bestResult = max(results, key=lambda x: x["dev"])
### END YOUR CODE
return bestResult
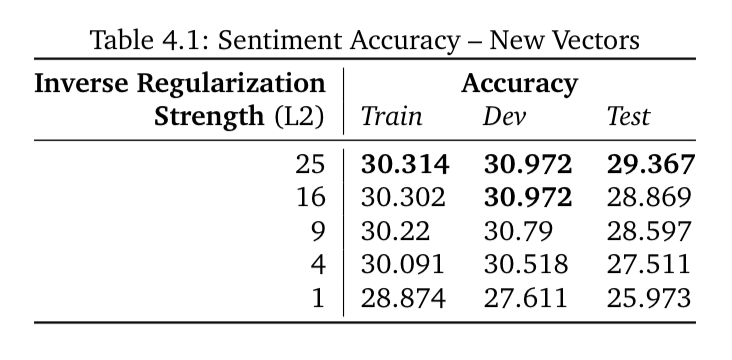
d 词向量的影响
用自己的词向量训练模型,与用GloVe预训练的词向量的模型作比较,为什么后者好?
自己的词向量:
GloVe的词向量:
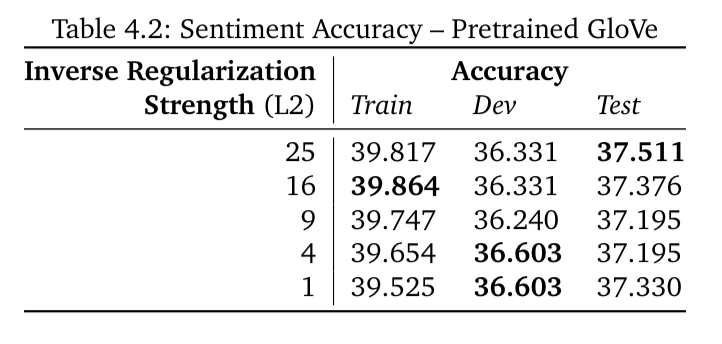
后者更好的原因是:
-
后者在维基上训练,数据量更大
-
后者维度更高(50维)
-
GloVe利用了全局统计信息,而word2vec(SG)没有
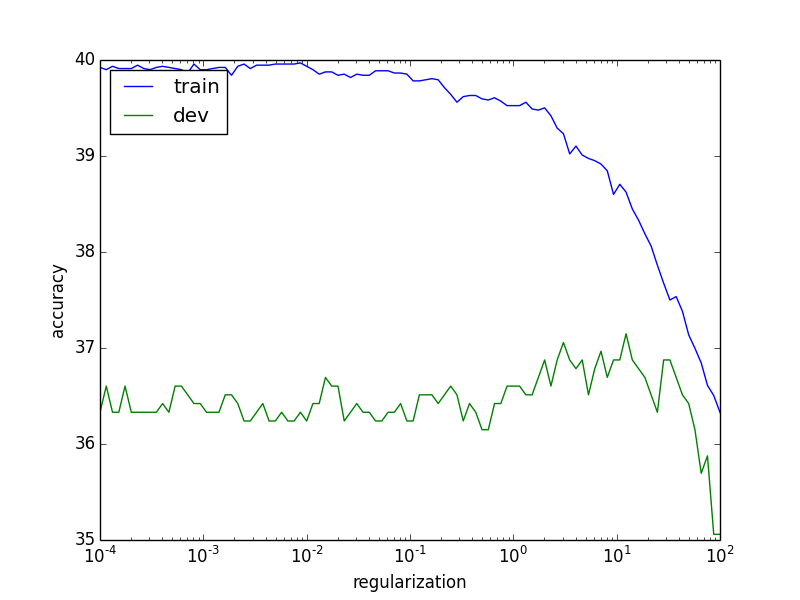
e 惩罚因子对效果的影响
f confusion matrix
脚本会自动生成confusion matrix:

这个矩阵的主对角线上的元素越多,说明预测越正确。其他元素都是失误。可见模型很难分辨“中性”情感,并倾向于将其分入负面。但模型没有犯下大是大非的错误(将--分入++,或反之)。
g 错误分析
查看q4_dev_pred.txt中的输出,想想看什么特征可能提高效果?
-
13nothing is sacred in this gut-buster .
说反话,词袋模型的软肋 -
31and if you 're not nearly moved to tears by a couple of scenes , you 've got ice water in your veins .
不理解习语“moved to tears”,不理解整句话
-
30... routine , harmless diversion and little else .
语料标注错误
Reference
https://github.com/hankcs/CS224n
https://github.com/rymc9384/DeepNLP_CS224N.git
 码农场
码农场
直接运行q3_run的话,得到的word_vector是保存在哪里? 运行了好像没找到输出文件啊
“负采样时的梯度推导” 对Vc求导中。里面的log怎么不见了?
请忽略这个问题。。。。
(1)gradcheck_naive函数中,numgrad = (new_f1 – new_f2) / (2 * h)这一行不应该是numgrad = (new_f1 – new_f2) / (2 * h)[ix]吗,然后后面才和grad[ix]比较呀?
(2)gradcheck_naive函数中31行,被除的分母max(1, abs(numgrad), abs(grad[ix]))啥意思?为啥不是直接拿误差和1e-5比较?
新手求解答,谢谢
应该是numgrad = ((new_f1 – new_f2) / (2 * h))[ix]
请问有人知道这个问题的吗?能不能解释一下,谢谢!
我认为3.a的原答案是对的,y_hat(算出每个词的概率)和y应该是W*1维,U是D*W维,那么U(y_hat – y)是对得上的。
感谢指正。
请问2.g里line 33 grad_h = sigmoid_grad(h) * dh, 为什么是求的sigmoid_grad(h)?
假设定义z=np.dot(data,W1) + b1,那么h = sigmoid(z),使用链式法则推导的时候有partial_h/partial_z = sigmoid(z)不是吗?
博主你好,请问2g部分里gradb2和gradb1是用什么公式求的?
The bias gradients for neuron $i$ on layer $k$ is simply $\delta^{(k)}_i$. And $\sum$ is for the average loss on whole batch.
negSamplingCostAndGradient 里面是不是有些问题之 indices你都没有使用到,而且采用的dataset.getSample 没有考虑到重复target word 的问题, 后面在计算器smalpe word的cost的时候 和assignment上面计算的公式有出入
$$
\begin{align} \sigma(x) &= \frac{1}{1 + e^{-x}} \\
\sigma(-x) &= \frac{1}{1 + e^{x}} \\
&=\frac{e^{-x}}{1 + e^{-x}}\\
&=1-\sigma(x)
\end{align}
$$
您好博主,请问2g部分29行 为什么yhat-labels之后还要除以data.shape[0],反向传播求出来的不就是直接yhat-y吗。除以data.shape[0]的作用是什么?
我来试着回答一下,这是因为28行的cost函数用的是average cross entropy,即除以data.shape[0]求平均,所以求导也会带着它,并不影响反向传播
可是代码要求部分,说的是Note: compute cost based on `sum` not `mean`.诶
我智障了,y是D×1维
说错了。。y的维数是W×1(有W个词),U的维数是D×W,U(y_hat – y)维数对的上
3.a 答案是对的吧,y的维数是D*1,U^T的维数是W×D,没有问题哇
3e部分的负采样与梯度,为什么不用源代码已经抽取的下标?为什么重新抽取下标?
太谢谢您了~!!
从课程官网下载的 assignment1.zip 中的 get_datasets.sh 脚本里面的数据集获取地址好像已经失效了,不知道博主的更新过的脚本是从哪里下载的?
你好,碰巧是跟你一个情况,昨天我也弄了好久。
博主提供的百度云网盘里有assignment1/u…/dataset这个文件夹。应该是下载了,拷贝过去就行。
兄弟,百度云盘的地址在哪? 没看见,只看到了github的地址。 我也发现那个sh文件的链接失效了–
博主关于cs224n发的第一个博文
glove那个数据集链接确实失效了,谷歌搜索一下`stanford glove`就能找到了
a部分中,yhat是D x 1, U是W x D才对
predicted是Dx1, target是Dx1, outputVectors是WxD, yhat是Wx1。这回没错了
我的理解是,$\boldsymbol{U} = [\boldsymbol{u}_{1}$,$\boldsymbol{u}_{1}$,$\dots$, $\boldsymbol{u}_{W}]$中的逗号应该表示按列拼接的意思,所以是$D \times W$。逗号和分号的意思不同,matlab中[1,2,3]是行向量,[1;2;3]才是列向量。
一个u表示一条单词的向量表示,Python中不以分号作为分隔,而且outputVector数量应是W个,向量维度是D
另外,在讲义中出现过$u_{c}^{T}\hat{v}$,所以$u$和$v$的维度应该都是一样的$D \times 1$
我也这么认为,看了前面neural network的那道题目中,weights维度的定义一般都是Dim(in) * Dim(out)的,然后outputVectors我输出了一下它的shape也是W*d,所以感觉博主这里的维度定义的不一样。
博主,3.a部分的为什么不是$z=U^\mathrm{T} \cdot v_c$,U的shape是D*W, $v_c$的shape是D*1。
你是对的