码农场
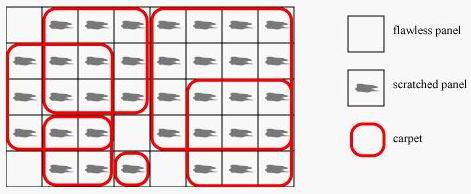
铺地毯：用最少的正方形覆盖所有点。
4.5开动脑筋智慧搜索
A*与IDA*
大致思路是预处理出一个覆盖所有点的正方形集合，最优解下界为所有点恰好能被最大正方形覆盖，然后IDA*搜索。
首先预处理，求出以某点为右下角的正方形最大边长。对于上图，该矩阵为
0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 2 2 3 3 3 3 3 1 2 3 0 1 2 3 4 0 1 2 1 0 1 2 3
进一步，若某个正方形完全包含在另一个正方形中，则排除这个正方形，因为我们要尽量少用正方形。
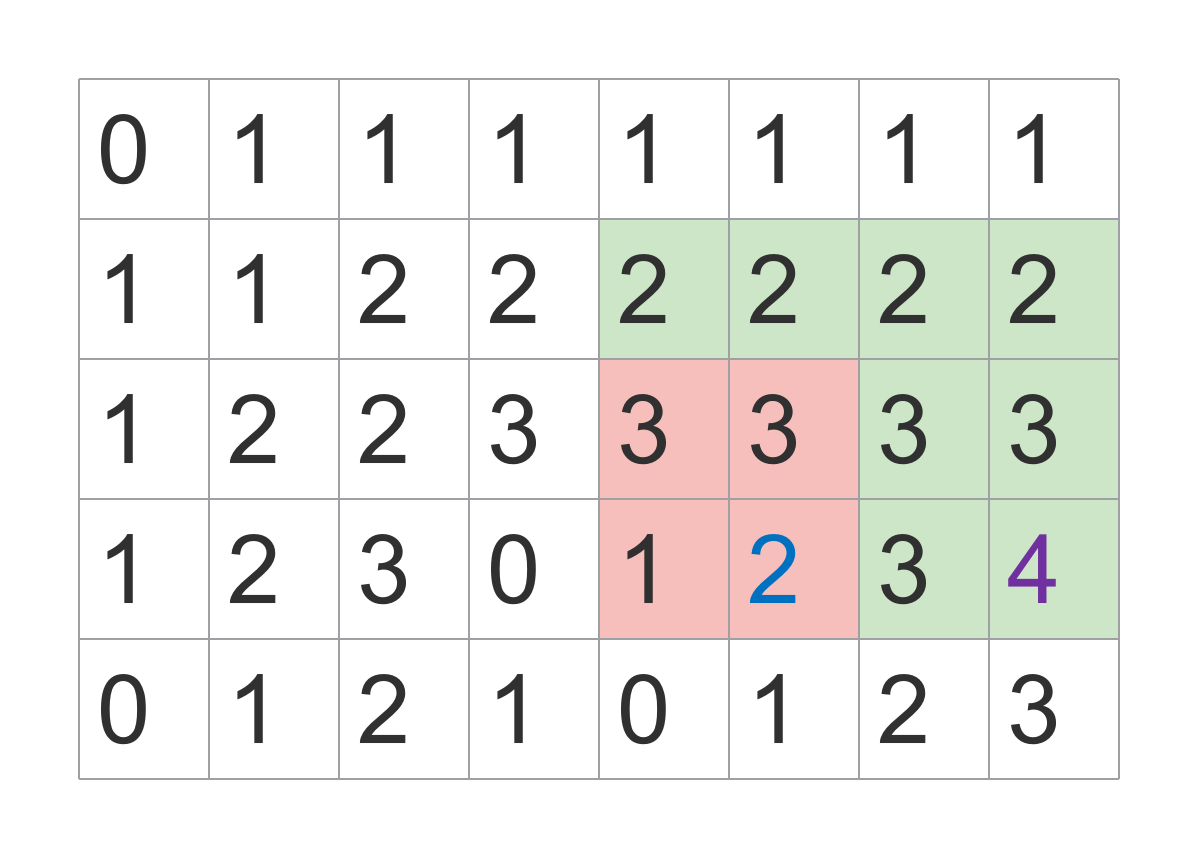
上图绿色正方形完全覆盖红色正方形，所以去掉红色正方形。去掉的操作很方便，简单将该元素设为0即可。
这一步得到：
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 3 0 0 0 0 3 0 0 0 0 4 0 0 2 1 0 0 0 3
接着统计每个点被几个正方形覆盖：
0 1 2 3 3 2 1 1 1 2 3 3 3 2 1 1 1 2 3 3 3 3 2 2 1 2 2 0 1 2 2 2 0 1 1 1 0 1 1 1
如果某个点只被一个正方形覆盖，则该正方形必选，记录下来；否则将该正方形加入搜索列表，从右下角往左上角搜索。
下界函数可以用这么一个简单的假设：将坏点视作流动的散沙，总能根据正方形变换形状，最后紧凑地流入一个个最大正方形中，返回用多少个最大正方形容器能够放得下剩余坏点，该数目即为当前情况下的最优解下界。
最后就是IDA*搜索了，这还算一道蛮能体现IDA*思想的题目。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define MAX_N 10
int ans, H, W, limit, // 最优解
max_w; // 正方形最大边长
int T[MAX_N][MAX_N], // T[y][x] := 以(x,y)为右下角的正方形最大边长
F[MAX_N][MAX_N], // 输入
X[MAX_N][MAX_N]; // 每个点被几个正方形覆盖
vector<pair<int, int> > v; // 正方形的右下角坐标
bool is_solved()
{
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
if (F[i][j] && X[i][j] == 0)
{
return false;
}
}
}
return true;
}
/**
* 当前所需正方形的下界
* @return
*/
int h()
{
int sum = 0;
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
if (F[i][j] && X[i][j] == 0)
{
sum++;// 需要覆盖但还没覆盖的点数
}
}
}
return sum / (max_w * max_w); // 假设这些点极其紧凑，形成一个个最大正方形
}
/**
* 搜索
* @param s 当前状态搜索的正方形个数
* @param cost 当前正方形个数
* @return 是否可行
*/
bool dfs(int s, int cost)
{
if (is_solved())
return true;
if (s >= v.size())
return false;
if (cost + h() >= limit)
return false;
for (int i = v[s].first + 1; i < H; i++)
{
for (int j = 0; j < W; ++j)
{
if (F[i][j] && X[i][j] == 0)
return false;
}
}
if (dfs(s + 1, cost)) // 不要s这个正方形
return true;
// 要s这个正方形
int X_backup[MAX_N][MAX_N];
memcpy(X_backup, X, sizeof(X));
int pi = v[s].first;
int pj = v[s].second;
int w = T[pi][pj];
for (int y = pi - w + 1; y <= pi; ++y)
{
for (int x = pj - w + 1; x <= pj; ++x)
{
X[y][x]++;
}
}
if (dfs(s + 1, cost + 1)) // 所以花费正方形个数+1
return true;
memcpy(X, X_backup, sizeof(X));
return false;
}
int ida_star()
{
if (max_w == 0)
return 0;
for (limit = h(); limit < 100; limit++)
{
if (dfs(0, 0))
return limit;
}
}
void init()
{
memset(T, 0, sizeof(T));
memset(X, 0, sizeof(X));
for (int i = 0; i < H; ++i)
{
T[i][0] = F[i][0];
}
for (int j = 0; j < W; ++j)
{
T[0][j] = F[0][j];
}
for (int i = 1; i <= H - 1; ++i)
{
for (int j = 1; j <= W - 1; ++j)
{
if (F[i][j])
{
T[i][j] = min(T[i - 1][j - 1], min(T[i - 1][j], T[i][j - 1])) + 1;
}
else
{
T[i][j] = 0;
}
}
}
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
int w = T[i][j]; // 最大正方形边长
for (int pi = i - (w - 1); pi <= i; ++pi)
{
for (int pj = j - (w - 1); pj <= j; ++pj)
{
if (i == pi && j == pj) // 遍历包含的某个正方形
continue;
int l = max(i - pi, j - pj); // 包含的某个正方形边长
if (w - l >= T[pi][pj])
{
T[pi][pj] = 0; // 完全包含，排除
}
}
}
}
}
int K[MAX_N][MAX_N]; // 每个点被几个正方形覆盖
memset(K, 0, sizeof(K));
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
if (T[i][j])
{
for (int y = i - T[i][j] + 1; y <= i; ++y)
{
for (int x = j - T[i][j] + 1; x <= j; ++x)
{
K[y][x]++;
}
}
}
}
}
v.clear();
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
if (T[i][j])
{
for (int y = i - T[i][j] + 1; y <= i; ++y)
{
for (int x = j - T[i][j] + 1; x <= j; ++x)
{
if (K[y][x] == 1) // 只被一个正方形覆盖，必选
{
for (int y = i - T[i][j] + 1; y <= i; ++y)
{
for (int x = j - T[i][j] + 1; x <= j; ++x)
{
X[y][x]++;
}
}
ans++;
T[i][j] = 0;
goto OUTER;
}
}
}
}
OUTER:;
}
}
max_w = 0;
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
if (T[i][j])
{
max_w = max(max_w, T[i][j]);
v.push_back(make_pair(i, j));
}
}
}
reverse(v.begin(), v.end()); // 从右下角往左上角搜索
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
while (scanf("%d%d", &W, &H), W)
{
for (int i = 0; i < H; ++i)
{
for (int j = 0; j < W; ++j)
{
scanf("%d", &F[i][j]);
}
}
ans = 0;
init();
printf("%d\n", ida_star() + ans);
}
#ifndef ONLINE_JUDGE
fclose(stdin);
#endif
return 0;
}
| 16519210 | hankcs | 2032 | Accepted | 196K | 0MS | C++ | 5008B | 2017-01-25 11:07:12 |
知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2032 Square Carpets 题解《挑战程序设计竞赛》