POJ 3155 Hard Life 题解 《挑战程序设计竞赛》

POJ 3155 Hard Life

心机婊：公司内部共 n 个员工，员工之间可能两两合不来。若员工u 和员工 v 有矛盾，用边(u, v)表示，共 m 个矛盾。突然大股东送来一个富二代，威胁到你的CEO宝座。你想分配给富二代一个垃圾团队，使得团队成员间的不团结率最高。不团结率定义为团队人员间的矛盾总数与被裁人员数的比值（不团结率 = 团队人员之间的矛盾总数 / 团队人员数）。

3.5借助水流解决问题的网络流

最小割

要最大化下式：

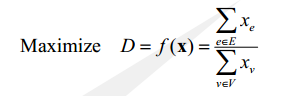
可以用二分求解以下分数规划问题：

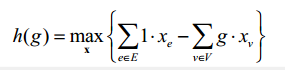
也就是最大化：

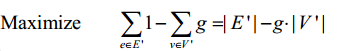
设子图为G'=(V', E')。如果边(u,v)∈E'，那么必有u,v属于V'。把点权设为负值的话，问题可以转换为求最大权闭合图(POJ 2987 Firing)。

又因为点固定时，边越多越好。所以转换思路，不是边E'决定点集V'，而应该反过来。当选定点集V'后，V'内部两两之间能构成的边就是最佳的E'。那么由V'发出的，不在E'内部的那些边构成了一个割集，当此割集最小时，E'最大。问题归结于求解最小割。

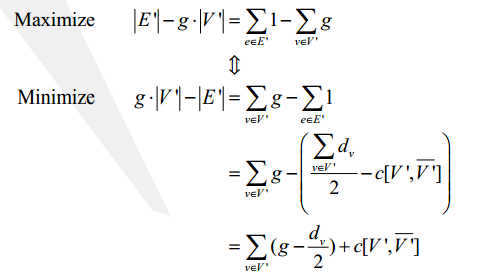
上图g为答案的猜测值，d为度数（出度+入度），c为割集（V'和V'补集构成的边）。

此时构图方式：

即是将原图 G(V , E) 转化为网络 N = (VN , EN ) 的过程：在原图点集V 的基础上增加源 s 和汇 t ；将每条原无向边 (u, v) 替换为两条容量为1的有向边u, v  和v,u  ；增加连接源 s 到原图每个点 v 的有向边s, v  ，容量为U ；增加连接原图每个点 v 到汇 t 的有向边v, t   ，容量为 (U + 2g ? dv ) 。

更加详细的证明和描述请参考《算法合集之《最小割模型在信息学竞赛中的应用》.pdf》：

这里给出基于dinic的实现：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

#define MAX_V 100 + 16
const double inf = 0x3fffffff;
const double eps = 1e-8;
int s, t, sum, degree[MAX_V], n, m;
bool visited[MAX_V];
typedef double cap_type;

// 邻接表用于表示边的结构体（终点、容量、反向边）
struct edge
{
	int to, rev;
	cap_type cap;
	edge(int to, cap_type cap, int rev) :to(to), cap(cap), rev(rev){}
};

// 边（起点，终点）
struct node
{
	int x, y;
}P[1024];

vector<edge> G[MAX_V];   // 图的邻接表表示
int level[MAX_V];      // 顶点到源点的距离标号
int iter[MAX_V];       // 当前弧，在其之前的边已经没有用了

// 向图中加入一条从from到to的容量为cap的边
void add_edge(int from, int to, cap_type cap)
{
	G[from].push_back(edge(to, cap, G[to].size()));
	G[to].push_back(edge(from, 0, G[from].size() - 1));
}

// 通过BFS计算从源点出发的距离标号
void bfs(int s)
{
	memset(level, -1, sizeof(level));
	queue<int> que;
	level[s] = 0;
	que.push(s);
	while (!que.empty())
	{
		int v = que.front(); que.pop();
		for (int i = 0; i < G[v].size(); ++i)
		{
			edge& e = G[v][i];
			if (e.cap > eps && level[e.to] < 0)
			{
				level[e.to] = level[v] + 1;
				que.push(e.to);
			}
		}
	}
}

// 通过DFS寻找增广路
cap_type dfs(int v, int t, cap_type f)
{
	if (v == t)
	{
		return f;
	}
	for (int& i = iter[v]; i < G[v].size(); ++i)
	{
		edge& e = G[v][i];
		if (e.cap > 0 && level[v] < level[e.to])
		{
			cap_type d = dfs(e.to, t, min(f, e.cap));
			if (d > eps)
			{
				e.cap -= d;
				G[e.to][e.rev].cap += d;
				return d;
			}
		}
	}

	return 0;
}

// 求解从s到t的最大流
cap_type max_flow(int s, int t)
{
	cap_type flow = 0;
	for (;;)
	{
		bfs(s);
		if (level[t] < 0)
		{
			return flow;
		}
		memset(iter, 0, sizeof(iter));
		cap_type f;
		while ((f = dfs(s, t, inf)) > eps)
		{
			flow += f;
		}
	}
}

void construct_graph(double g)
{
	for (int i = 0; i < MAX_V; ++i)
	{
		G[i].clear();
	}
	for (int i = 1; i <= n; i++)
	{
		add_edge(s, i, m);
		add_edge(i, t, m + 2 * g - degree[i]);
	}
	for (int i = 0; i < m; i++)
	{
		add_edge(P[i].x, P[i].y, 1.0);
		add_edge(P[i].y, P[i].x, 1.0);
	}
}

// 遍历
void dfs_travel(int v)
{
	++sum;
	visited[v] = true;
	vector<edge> gv = G[v];
	for (vector<edge>::iterator it = gv.begin(); it != gv.end(); ++it)
	{
		const edge &e = *it;
		if (e.cap > eps && !visited[e.to])
		{
			dfs_travel(e.to);
		}
	}
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	scanf("%d%d", &n, &m);
	if (m == 0)
	{
		printf("1\n1\n");
	}
	else
	{
		s = 0, t = n + 1;
		for (int i = 0; i < m; ++i)
		{
			scanf("%d%d", &P[i].x, &P[i].y);
			degree[P[i].x]++;
			degree[P[i].y]++;
		}
		// 二分求解分数规划
		double lb = 0, ub = m, mid, hg;
		const double precision = 1.0 / n / n;
		while (ub - lb >= precision)		//	误差的精度不超过1 / (n * n)
		{
			mid = (lb + ub) / 2;
			construct_graph(mid);
			hg = (n * m - max_flow(s, t)) / 2;
			(hg > eps ? lb : ub) = mid;
		}
		construct_graph(lb);				//	mid不一定满足h(mid) > eps,但是lb一定满足
		max_flow(s, t);
		sum = 0;
		dfs_travel(0);
		printf("%d\n", sum - 1);
		for (int i = 1; i <= n; ++i)
		{
			if (visited[i] == true)
			{
				printf("%d\n", i);
			}
		}
	}

#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3155 Hard Life 题解 《挑战程序设计竞赛》