CS224n笔记5 反向传播与项目指导

最后一次数学课，其实都是些很基础的推导而已。从四个不同的层面讲解反向传播，其中电路和有向图类比还是很直观新颖的解释。

任意层的通用公式

第$l$层的残差：

$$\delta^{(l)} = (W^{(l)T} \delta^{(l+1)}) \circ f'(z^{(l)})$$

其中$f$是激活函数：

$$ f(z) = \frac{1}{1 + e^{-z}}$$

对于顶层来讲，残差就是根据某个损失函数得到的误差。对于底层来讲，激活函数不存在，或相当于$f(x)=x$。

$z$是线性函数：

$$z^{(l)}=W^{(l-1)}a^{(l-1)} + b^{(l-1)}$$

而$\circ$是相同大小的向量之间的element wise product($\circ : \mathbb{R}^N \times \mathbb{R}^N \rightarrow \mathbb{R}^N$)

正则化的损失函数关于第$l$层的权值矩阵的梯度：

$$\frac{\partial}{\partial W^{(l)}}E_R=\delta^{(l+1)}(a^{(l)})^T+\lambda W^{(l)}$$

关于第$l$层的偏置的梯度：

$$\frac{\partial}{\partial b^{(l)}}E_R=\delta^{(l+1)}+\lambda b^{(l)}$$

其中，$a$是激活值：

$$a^{(l)}=f(z^{(l)})$$

这里偏置单元与普通神经元在数学上并无不同，只不过由于激活值$a^{(l)}=1$，所以可以把激活值省略掉。

反向传播的电路解释

比如函数$f(x,y,z) = (x + y) z$可视作如下加法器和乘法器电路：

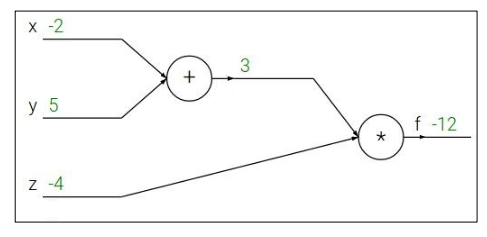
定义$q = x + y$ 、 $f = q z$，于是有$\frac{\partial q}{\partial x} = 1, \frac{\partial q}{\partial y} = 1$ 和$\frac{\partial f}{\partial q} = z, \frac{\partial f}{\partial z} = q$。求$\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}$

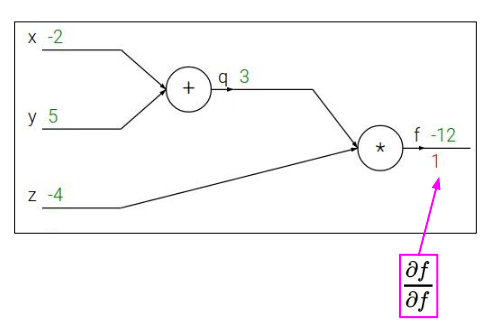
我们可以从输出到输入反向计算，先得到输出关于输出自己的导数：

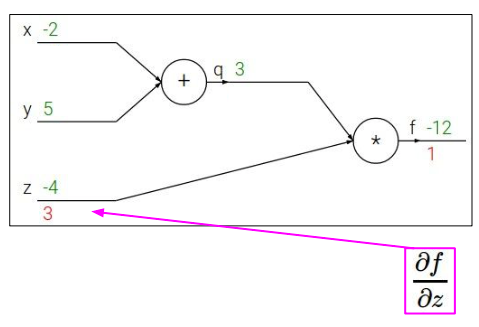
然后得到$f$关于$z$的导数：

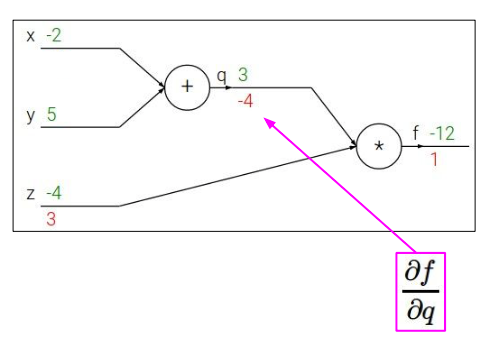
另一条路，$f$关于$q$的导数：

$f$关于$y$的导数：

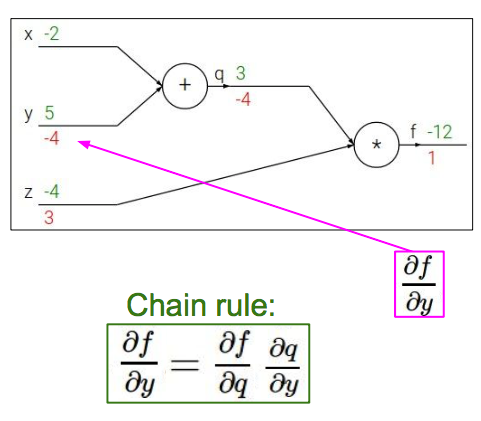
$f$关于$x$的导数：

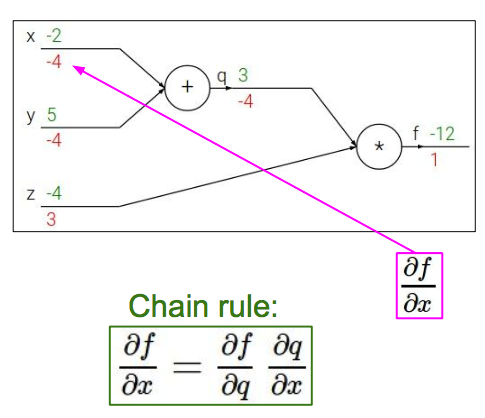
这种反向回溯的过程放到神经元中就是反向传播了：

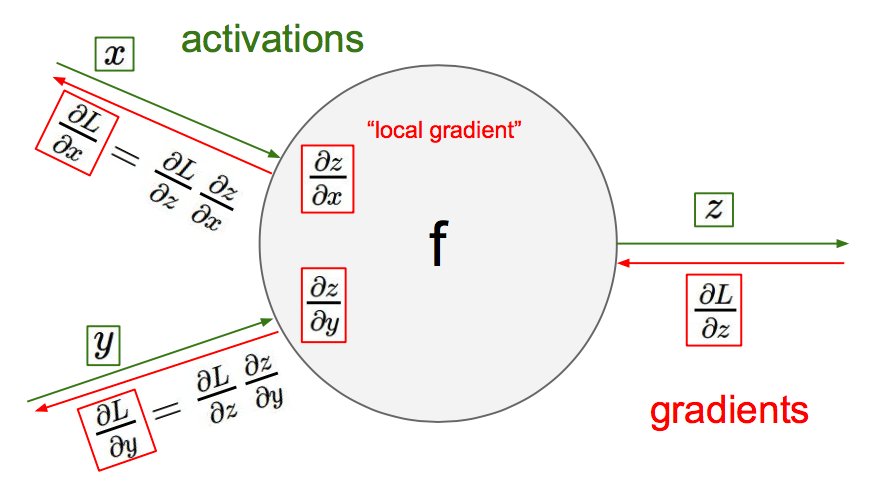
反向传播时每通过一级，就用链式法则乘以这一级的导数。

另一个稍微复杂一点的例子：

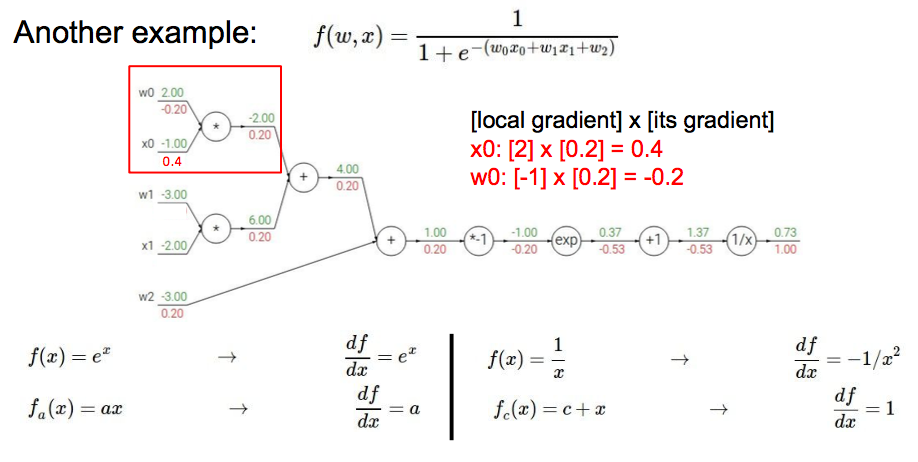
其中，sigmoid相关的元件可以合并为一个sigmoid gate：

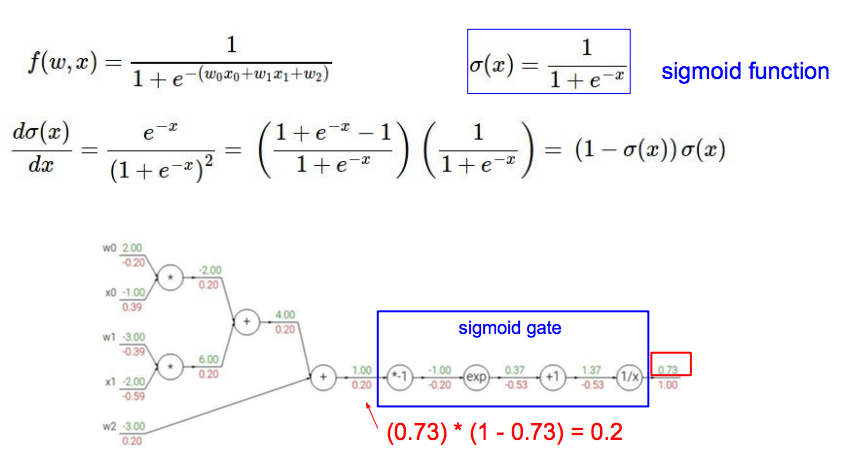
第三种理解：流程图

将上述电路视作有向无环流程图去理解链式法则，比如一条路径：

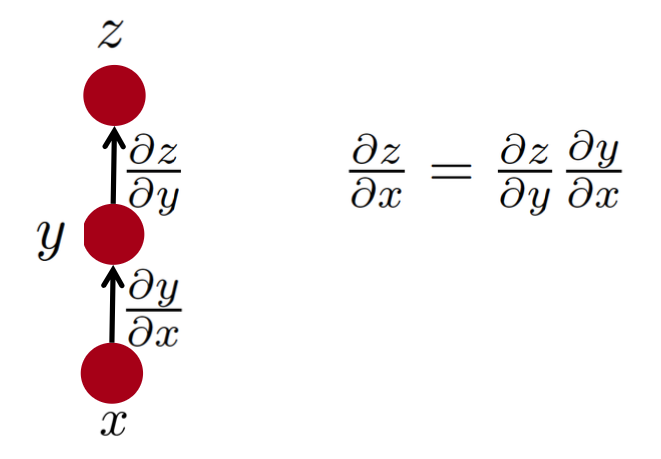
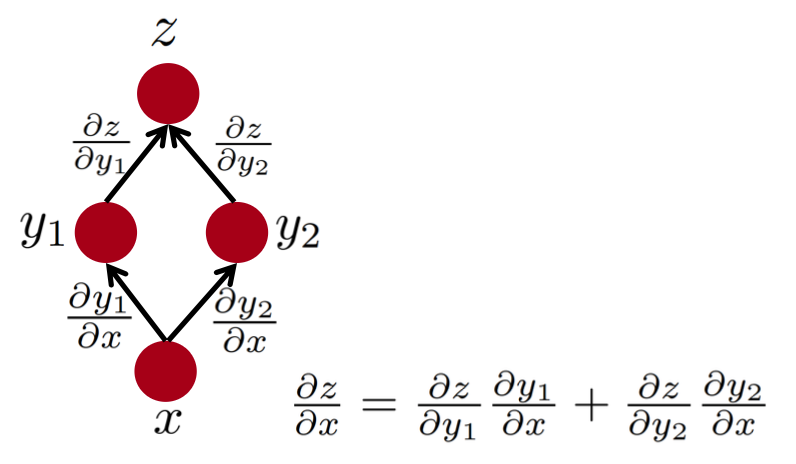
2条路径：

推广到多条路径：

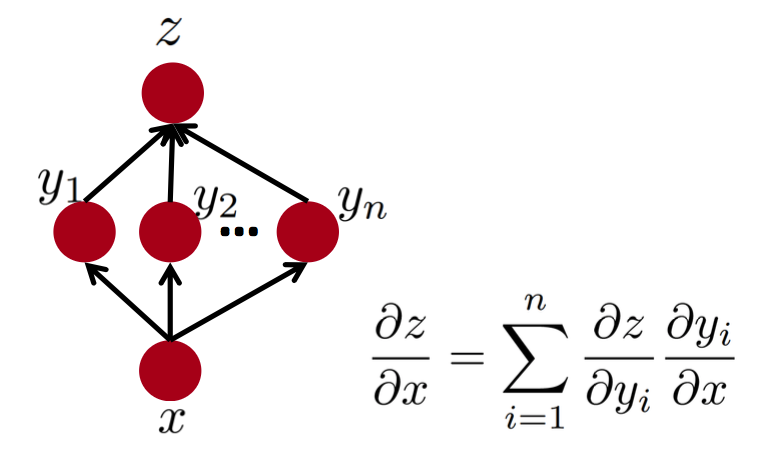
推广到更复杂的流程图：

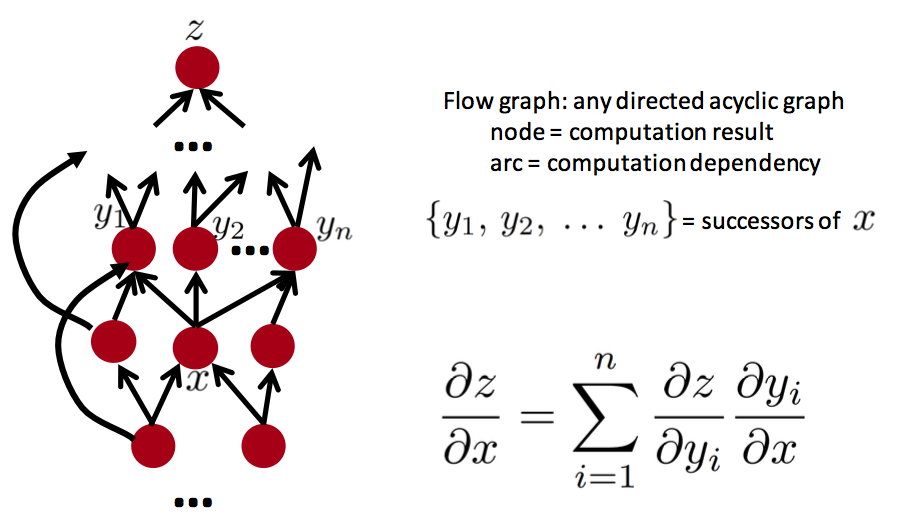
只要找到z的所有父节点应用链式法则并求和即可。

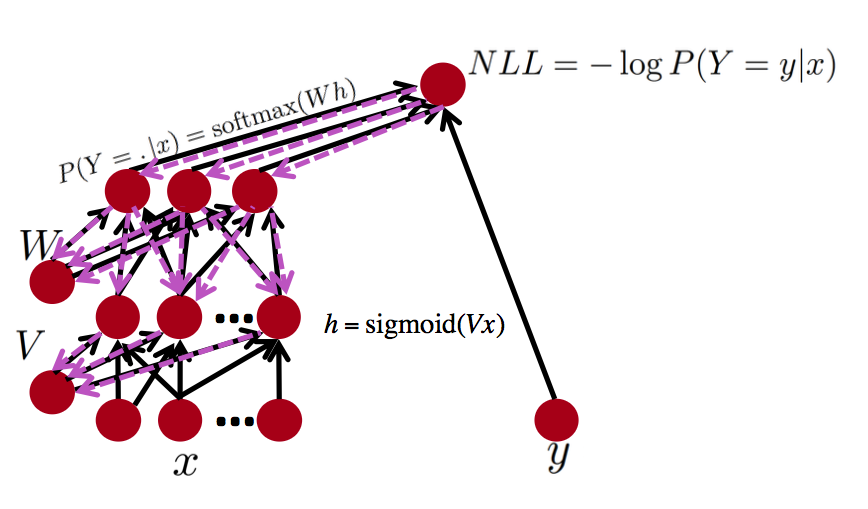
神经网络可以视作流程图的一个实例：

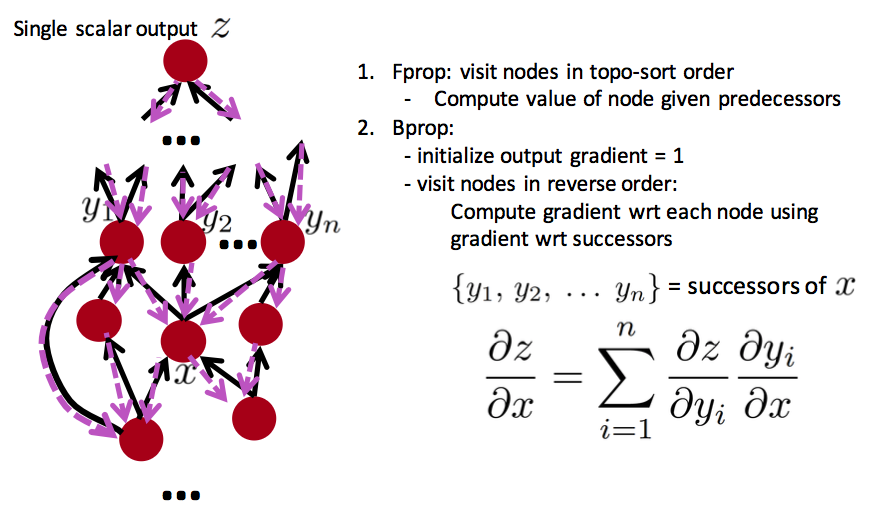
任意流程图都可以执行反向传播：

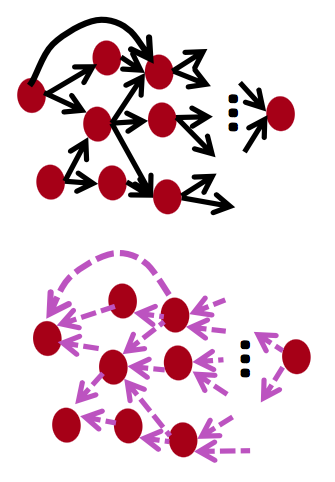
现在有一些软件包（TensorFlow）可以自动从前向传播的symbolic expression（符号表达式）推导梯度，适用于快速设计原型。（其实matlab里也可以）

第四种解释：实际神经网络中的误差信号

其实就是把上面这些解释综合起来的解释，对如下2层的网络来讲：

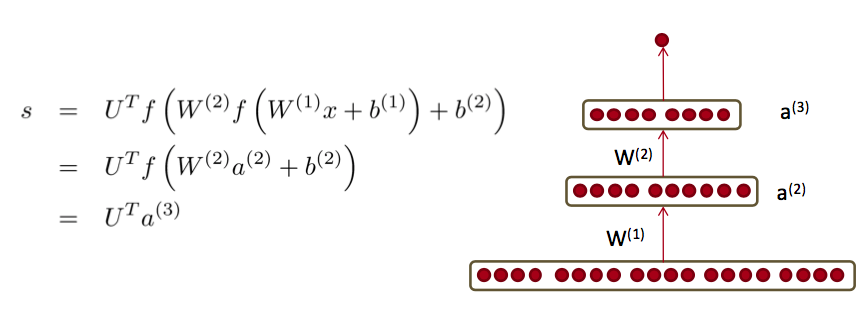
假设最后一层对$z^{(3)}$的误差是$\delta^{(3)}$：

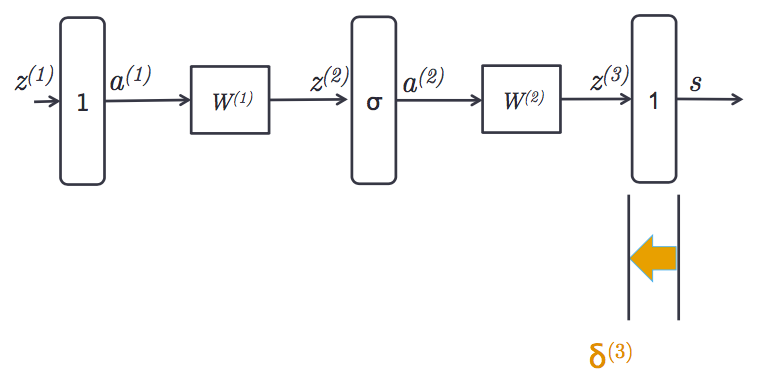
于是对$W^{(2)}$的导数是$\delta^{(3)}a^{(2)T}$

通过线性乘法器，对$a^{(2)}$的导数是权值与$\delta^{(3)}$的乘积：

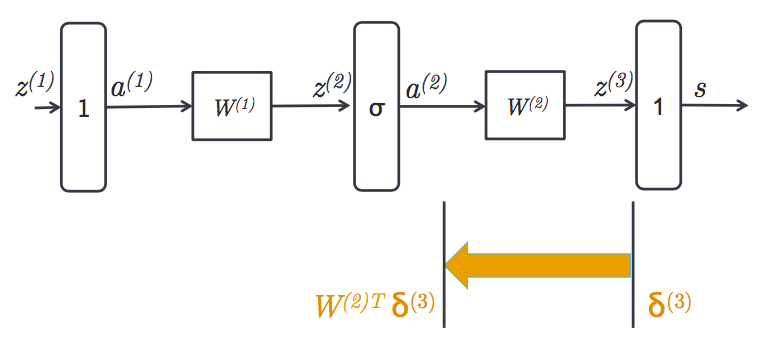
通过一个sigmoid gate，对$z^{(2)}$的导数是：

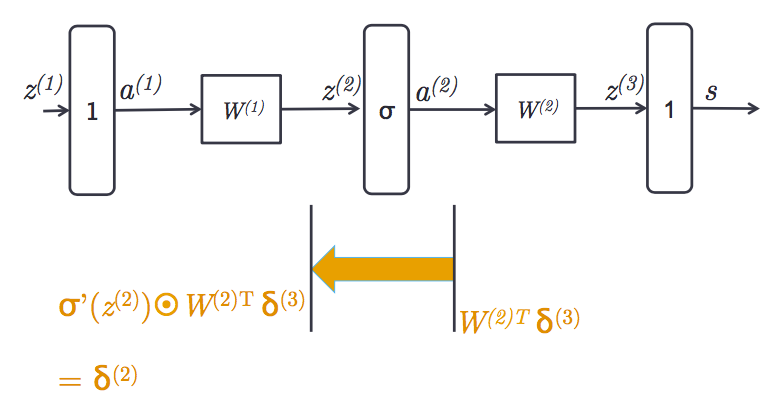
再通过一个线性乘法器，得到对$a^{(1)}$的导数：

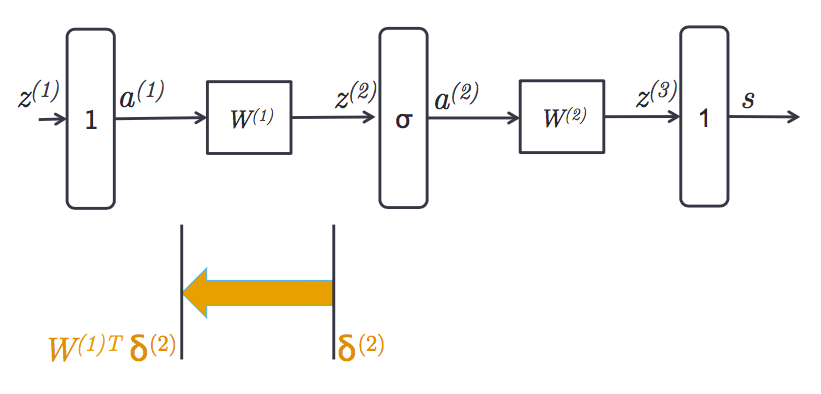
于是对$W^{(1)}$的导数是 $\delta^{(2)}a^{(1)T}$。

课程项目

接下来都是围绕着课程项目的指导与建议，就不啰嗦了。简单写写一些体会：

• 不要想着一上来就发明个新模型搞个大新闻

• 也不要浪费大部分时间在爬虫上面，本末倒置

• 把旧模型用于新领域\新数据也是不错的项目

• 先要按部就班地熟悉数据、熟悉评测标准、实现基线方法

• 再根据基线方法的不足之处思考深度学习如何能带来改进

• 再实现一个已有的较为前沿的模型

• 观察该模型犯的错误，思考如何改进

• 这时才能没准就福至心灵发明一个新方法

 知识共享署名-非商业性使用-相同方式共享：码农场 » CS224n笔记5 反向传播与项目指导