近来预训练语言模型在许多任务上成果斐然,然而在多任务联合学习上则差强人意。通过剪枝,我们发现所有任务会争夺一些通用的注意力头。据此,我们提出了干细胞假说:预训练会孕育一些天才注意力头,如同干细胞,可以分化为专精一种任务的功能细胞,却难以同时分化为全才细胞。为了验证该假说,我们设计了一些新奇的探针,剖析了预训练注意力头在单任务/多任务预训练前后的变化。![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
这是我们在EMNLP2021上的长论文,不同于搭网络刷榜的风格,我们试图打开Transformer的黑盒子一探究竟。本来不准备介绍的,因为这项工作存在很多局限性。但在这个年代大家对SOTA的关注太高了,如果我们这些小众研究不发声,估计一点浪花都激不起。所以写篇博客简要介绍我们的新发现,在语言上偏向通俗活泼,并非原论文的中译,可能存在许多表述上的不规范或不严谨。感兴趣的朋友欢迎阅读原论文,我们的代码已经开源。
多任务学习的困境
自从18年BERT问世以来,预训练Transformer编码器产生的上下文相关词嵌入取代了word2vec等静态词嵌入,成为几乎每个NLP模型的标配。虽然原地带来3个点左右的提升,然而算力开销也是不菲。一种自然而然的解决方案是联合学习(MTL,multi-task learning)(Clark et al., 2019b):通过多个任务共享同一个编码器来分摊编码的开销,常用的hard-parameter sharing模型架构如下:
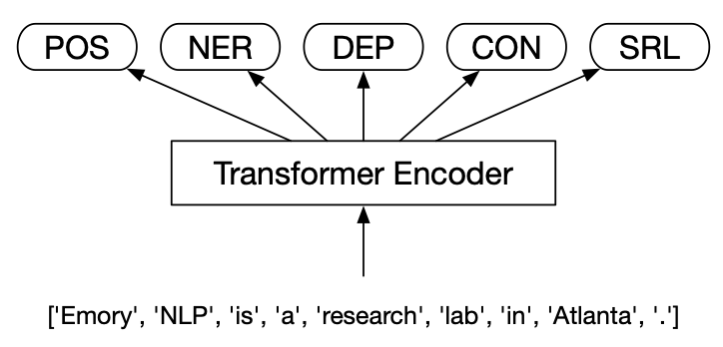
比如HanLPv2.1实现的多任务框架,就支持了10种子任务的联合学习:

然而绝大多数联合学习工作都有局限:要么任务的数量只有两三个、要么任务解码器同质化严重(都是MLP)、要么任务相关性非常高(比如命名实体识别和关系分类),给大众造成的印象是MTL不但省开销,而且能相互促进每个子任务。
我们在OntoNotes数据集5个核心NLP任务(POS:词性标注、NER:命名实体识别、DEP:依存句法分析、CON:成分句法分析、SRL:语义角色标注)上的试验发现,完全不是这么回事。哪怕用上了数据集重采样,损失动态均衡等手段也是无济于事。
这是BERT的结果,表格第一部分主对角线为单任务学习,否则为两两联合学习,最后一列为5个任务联合学习:
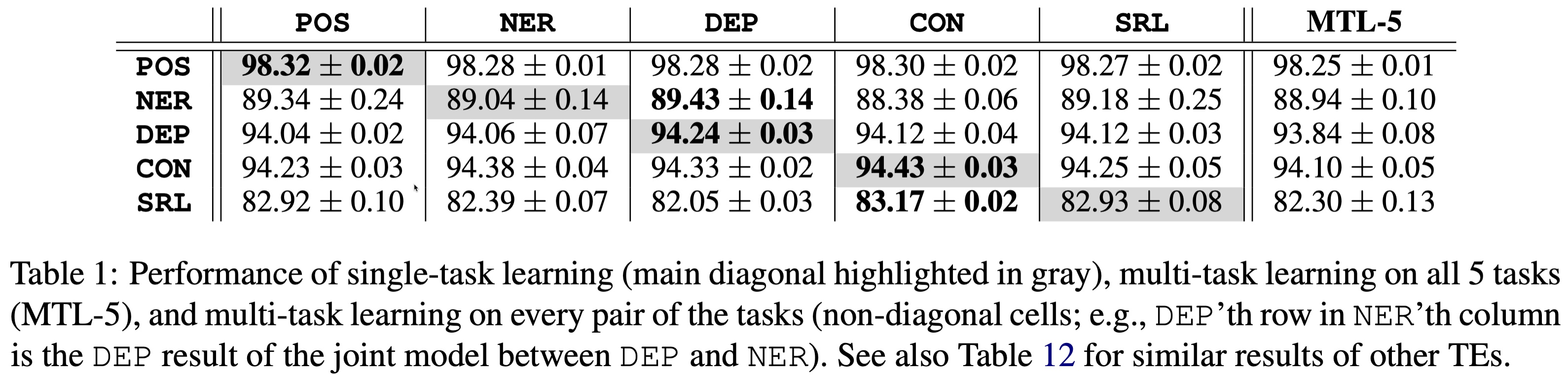
可见单任务(STL)一般准确率最高;双任务之间可能提高一个,但一定降低了另一个,可谓损人利己;而5个任务联和的效果几乎垫底。类似地,我们在最新发布的RoBERTa、ELECTRA和DeBERTa上也发现了类似的结果:
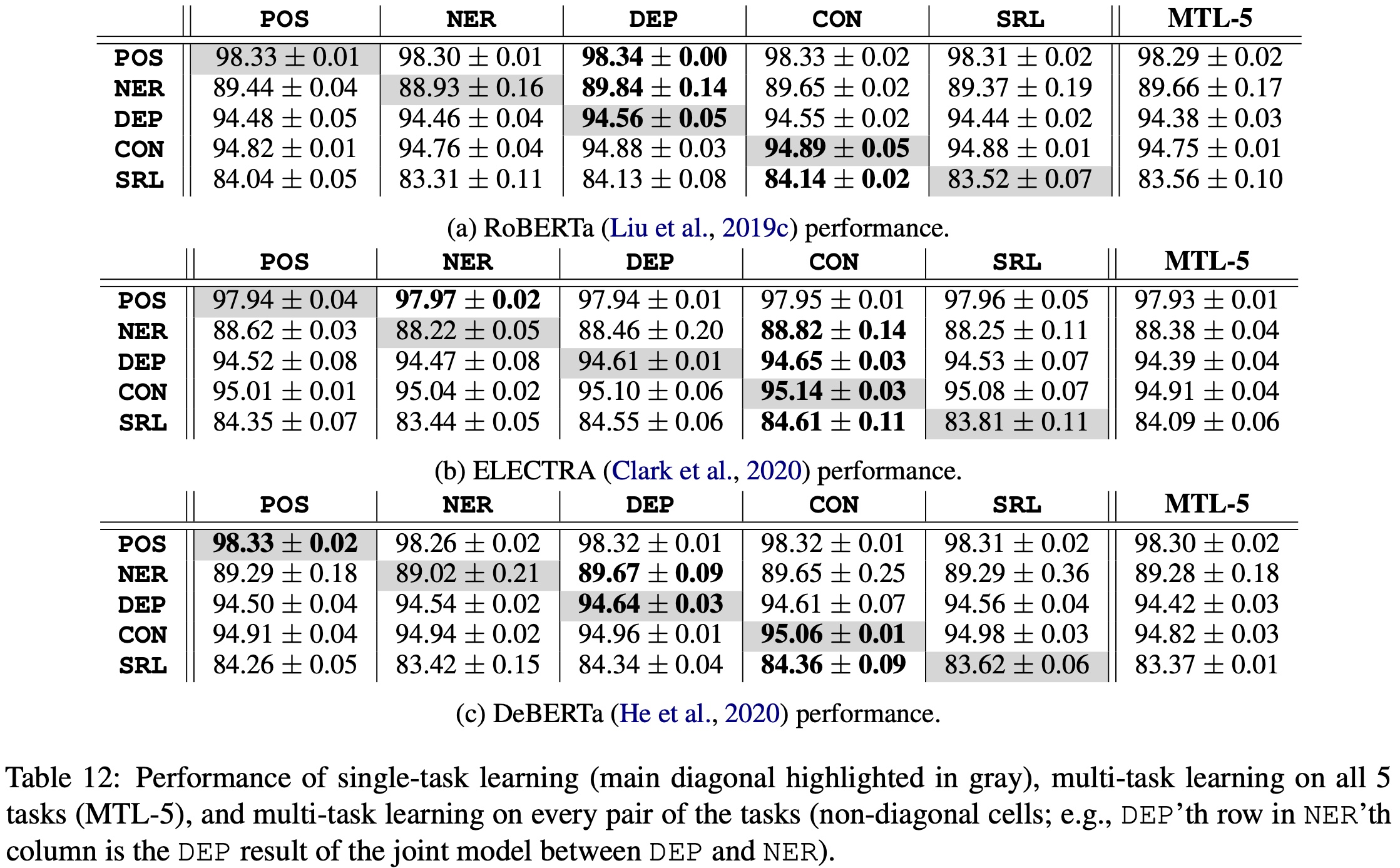
剪枝分析
我们隐隐猜测Transformer的注意力头可能出了问题,于是决定利用剪枝技术去分析每个任务到底需要哪些注意力头。我们为每个注意力头添加一个二进制阀门$z_j$,用该二进制阀门乘以该注意力头的输出。如果一个注意力头没有用处,阀门取$0$,否则取$1$。用公式描述如下:
$$\newcommand{\mask}{\mathbf{z}}\begin{equation*}
\text{Attention}^{(j)}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = z_j \cdot \text{softmax}(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d_k}})\mathbf{V}
\end{equation*}$$
由于这些二进制$\mask=\{z_j : \forall_{j = [1, \ell]}\}$ ($\ell$: 注意力头的总数)是离散的,所以无法用梯度方法学习。所以我们采用$\def\bm#1{\boldsymbol{#1}}
\bm{L_0}$正则化技术,将每个$z_j$ relax成一个连续随机分布。具体说来,将$\mathbf{z}$的累积密度函数的反函数参数化为$G_{\bm{\alpha}}(\mathbf{u})$,其中$\bm{\alpha}$为待学习的参数。也就是说,如果$z$大部分的概率质量位于$0$或者$1$的话,往$G_{\bm{\alpha}}(\mathbf{u})$里输入概率,就能得到$\mathbf{z}$的近似取值。接下来,只要将$[0,1]$区间的概率均匀采样一遍,就能估计到$\mathbf{z}$的平均值了,也就是:
$$\newcommand{\mask}{\mathbf{z}}
\mathbf{u} \sim U(0,1) \quad\Rightarrow\quad \mask = G_{\bm{\alpha}}(\mathbf{u})$$
其中$\mathbf{u} = \{u_j : \forall_{j = [1, \ell]}\}$为独立同分布采样。我们选择一种值域介于$[0,1]$之间,且大部分概率质量位于两端的Hard Concrete Distribution (Louizos et al., 2018)作为$\mathbf{z}$的分布。该分布示意图(图源)如下:
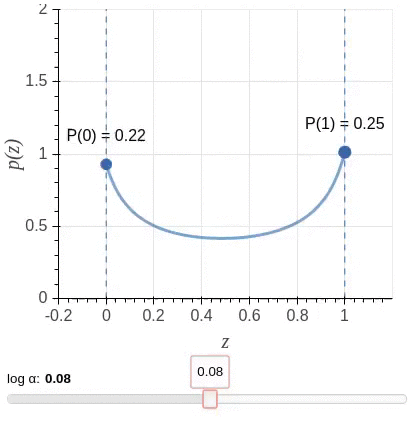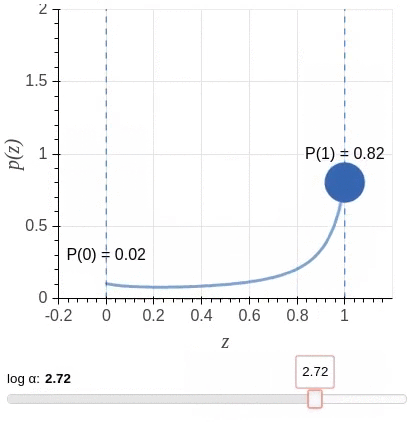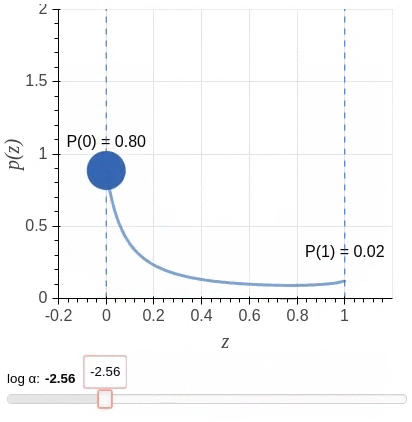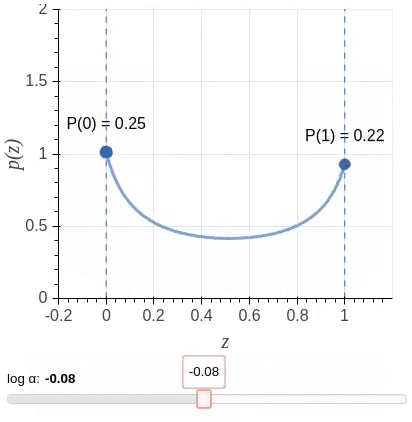
用公式描述如下:
$$\begin{align*}
g_{\bm{\alpha}}(\mathbf{u}) &=\text{sigmoid}(\log \mathbf{u} - \log(\mathbf{1}-\mathbf{u}) + \bm{\alpha}) \\
G_{\bm{\alpha}}(\mathbf{u}) &= \min(\mathbf{1}, \max(\mathbf{0}, g_{\bm{\alpha}}(\mathbf{u}) \times (r - l) + l))
\end{align*}$$
通过采样$\mathbf{u}$进行蒙特卡洛近似,我们得到了$\mask$的均值以及$\bm{L_0}$正则损失:
$$\begin{align}
\label{eq:l0-loss}
\begin{split}
\mathbb{E}_{\,\mathbf{u} \sim U(0,1)}\left[\mask\right]&=\text{sigmoid}\left( \bm{\alpha} - \log\frac{-l}{r}\right) \\
\mathbb{E}_{\,\mathbf{u} \sim U(0,1)}\left[ L_0 \right] &= \sum_{j=1}^n \mathbb{E}\left[ z_j\right] \\
\end{split}
\end{align}$$
接着将正则损失加到任务损失上就可以利用SGD优化了。
剪枝策略
已存在的剪枝方法是静态剪枝static pruning (SP),也就是冻结解码器,然后对编码器剪枝的做法。静态剪枝的缺点是你得先训练一个模型,然后执行剪枝,花费了双倍的时间。
我们要跑的试验太多了,于是提出动态剪枝dynamic pruning(DP),也就是不冻结解码器,一边训练一边剪枝。剪枝的过程如下所示:
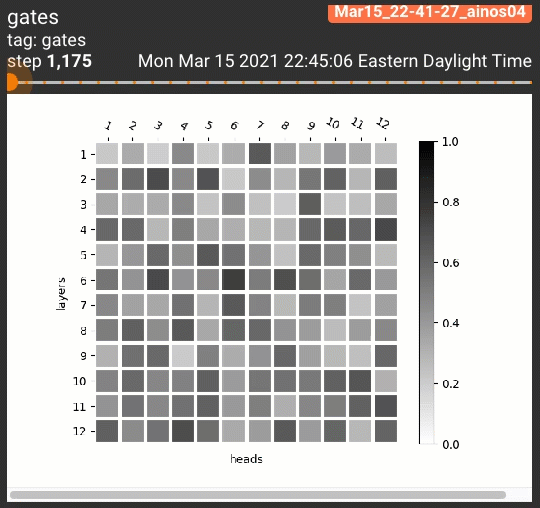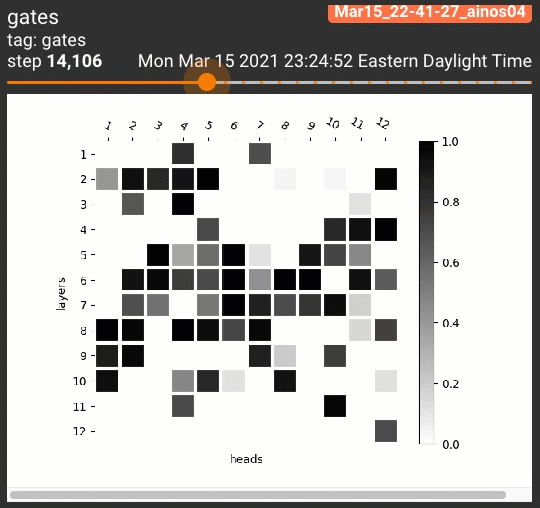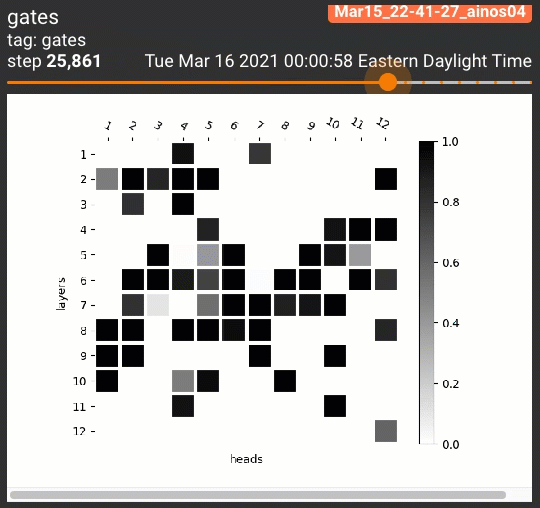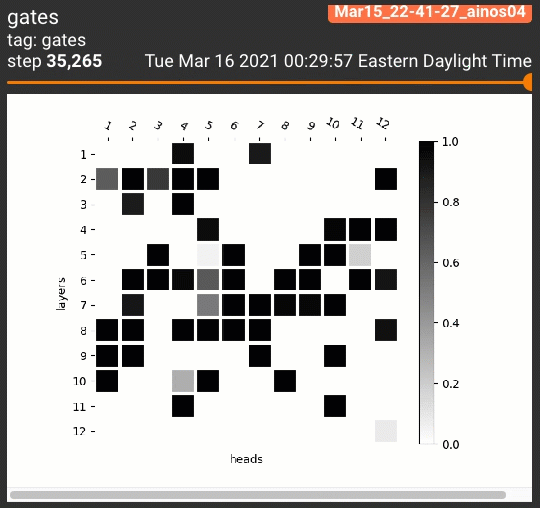
剪枝试验
我们对每种试验跑三次取平均值,对BERT的剪枝结果如下所示: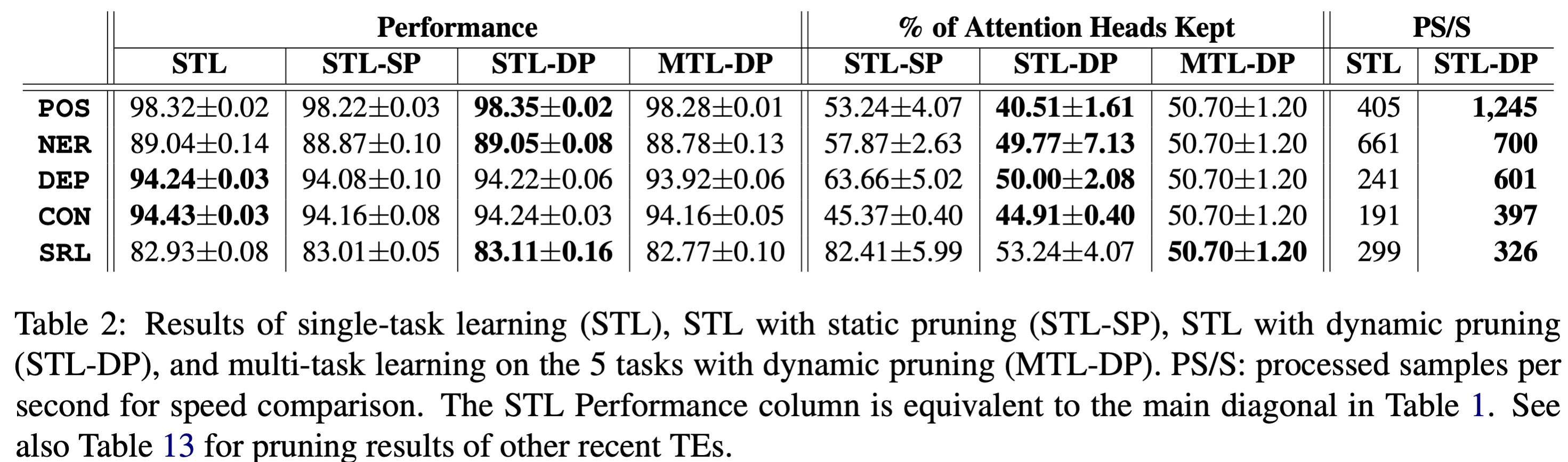
对其他Transformer的剪枝,也得到了类似的结果: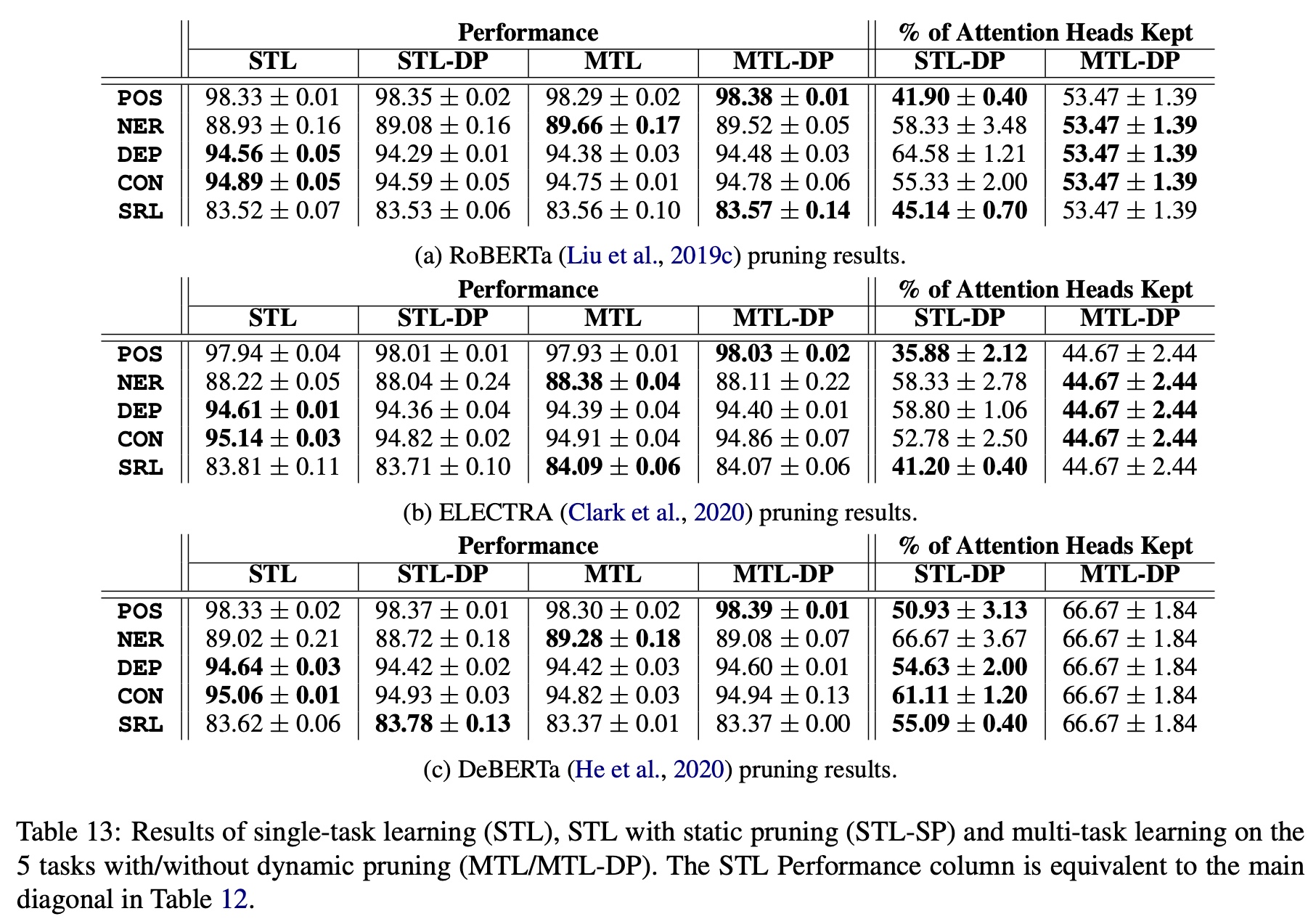
可见STL-DP可以在比STL-SP剪切更多注意力头的基础上,得到更高的准确率,有时候甚至比STL更高。另外,剪枝后的模型跑得显著更快。
可视化
为了一览剪枝后的注意力头的位置分布,我们设计了两种可视化策略。针对跑三次的试验,我们将每次每个注意力头的阀门取值依次分配到RGB的一个通道上:
$$\mathrm{R/G/B}_{j,t} = 255 \times (1 - {z}^{(1/2/3)}_{j,t})$$
对5个任务共计15次试验的每个注意力头,我们平均了它的阀门取值,制作了灰度图:
$$H_j = \frac{1}{15} \sum_{r=1}^3 \sum_{t=1}^5 z^{(r)}_{j,t}$$
无论哪种策略,黑色都表示一个注意力头被多个试验重复利用。这些可视化策略产生的结果如下:

令人惊讶的是,几乎所有STL/MTL的多次试验都反复用到了同一组注意力头(图中的黑色方格,如同一个字母M)!我们还定性地分析了这些阀门在各组试验中的相关性,发现总体在70%到90%之间:
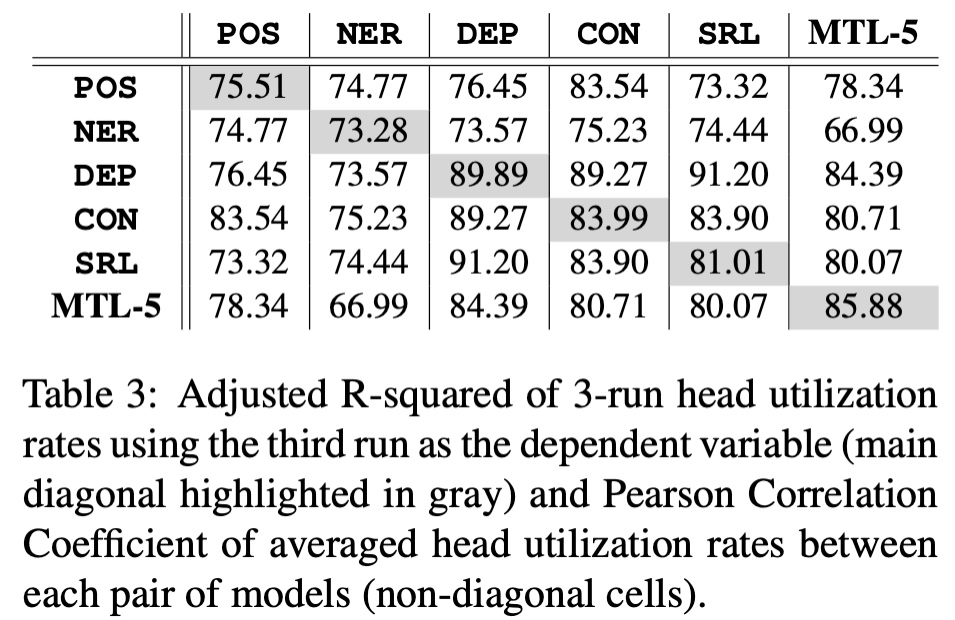
其他Transformer也展示了类似的结果:


这种奇妙的重合说明了三个事实:
-
注意力头的利用率在同一模型不同的随机试验中是重合的。
-
注意力头的利用率在不同任务之间是重合的。
-
注意力头的利用率在单任务和多任务之间还是重合的。
在所有情况下,Transformer都选择利用相同的一组注意力头。由于多头注意力机制的设计初衷是利用多个注意力头提取样本在不同的小空间里的表示融合成一个多样化的表示,每个注意力头的参数量很小,也就是说每个注意力头的容量是有限的。既然一个注意力头被多个任务同时利用,并且它的容量是有限,那么必然会造成塞不下的问题。据此,我们提出“干细胞假说”:
在预训练Transformer中存在一组“干细胞”注意力头,由于它们被同时用于多个任务,故无法同时满足差异性较大的多个任务。
探针分析
为了验证我们的假说,我们决定设计一些探针来检测每个注意力头在单任务或多任务学习前后的变化。由于我们试验的模型实在太多了,并且我们关注单个注意力头,所以不采用需要训练的探针,而是采用或者设计了很多无参的探针。
探针方法
注意力探针
针对DEP和SRL,我们采用了直接查看注意力矩阵的探测方法。对DEP来讲,我们计算head和dependent相互注意的比例:
$$\begin{align*}
\frac{1}{n} \sum_{\forall (h,d)} \bm{1}{ \left(\mathbf{g}_{h} =d \parallel \mathbf{g}_{d} =h \right) }
\end{align*}$$
对SRL来讲,我们计算谓词和论元中任意单词之间相互注意的比例:
$$\begin{equation*}
\frac{1}{m} \sum_{\forall p, \forall T^p} \bm{1}{ \left(\mathbf{g}_{p} \in T^p \parallel \exists\: t \in T^p : \mathbf{g}_t = p \right) }
\end{equation*}$$
注意力结果探针
针对POS/NER/CON我们设计了一种“伪聚类”的探针:计算注意力头对每种label的单词的特征的质心,然后计算每个单词最近的质点的标签与它真实标签相符的比例:

探针试验
我们直接对之前训练的模型执行上述探针,发现了如下两个结论。
存在天才干细胞
在预训练BERT上,哪怕不进行下游任务的微调,有一些注意力头的准确率已经非常高。比如DEP: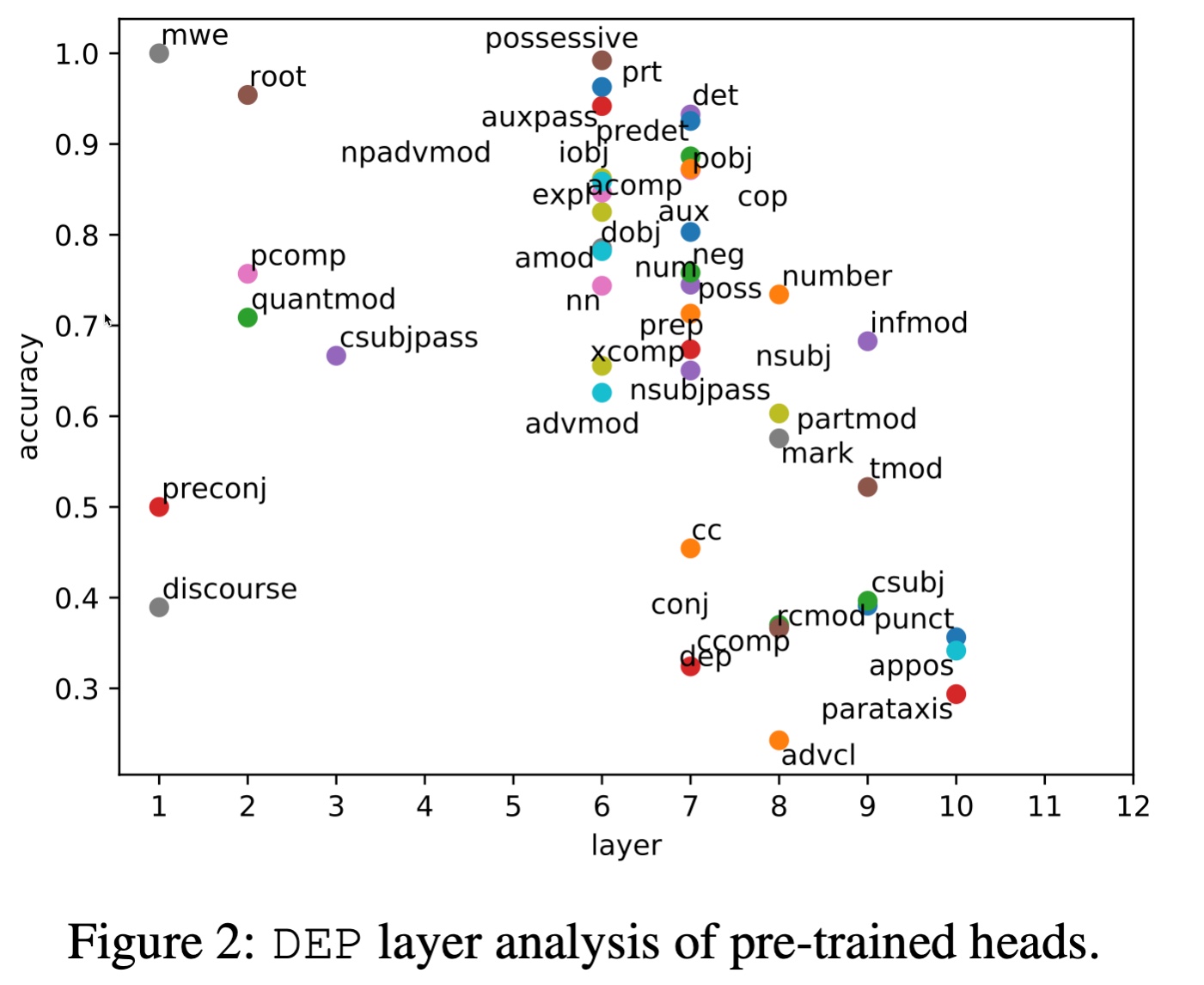
有些标签的准确率已经达到了90%以上,而且在很底层的layer上面。再比如SRL: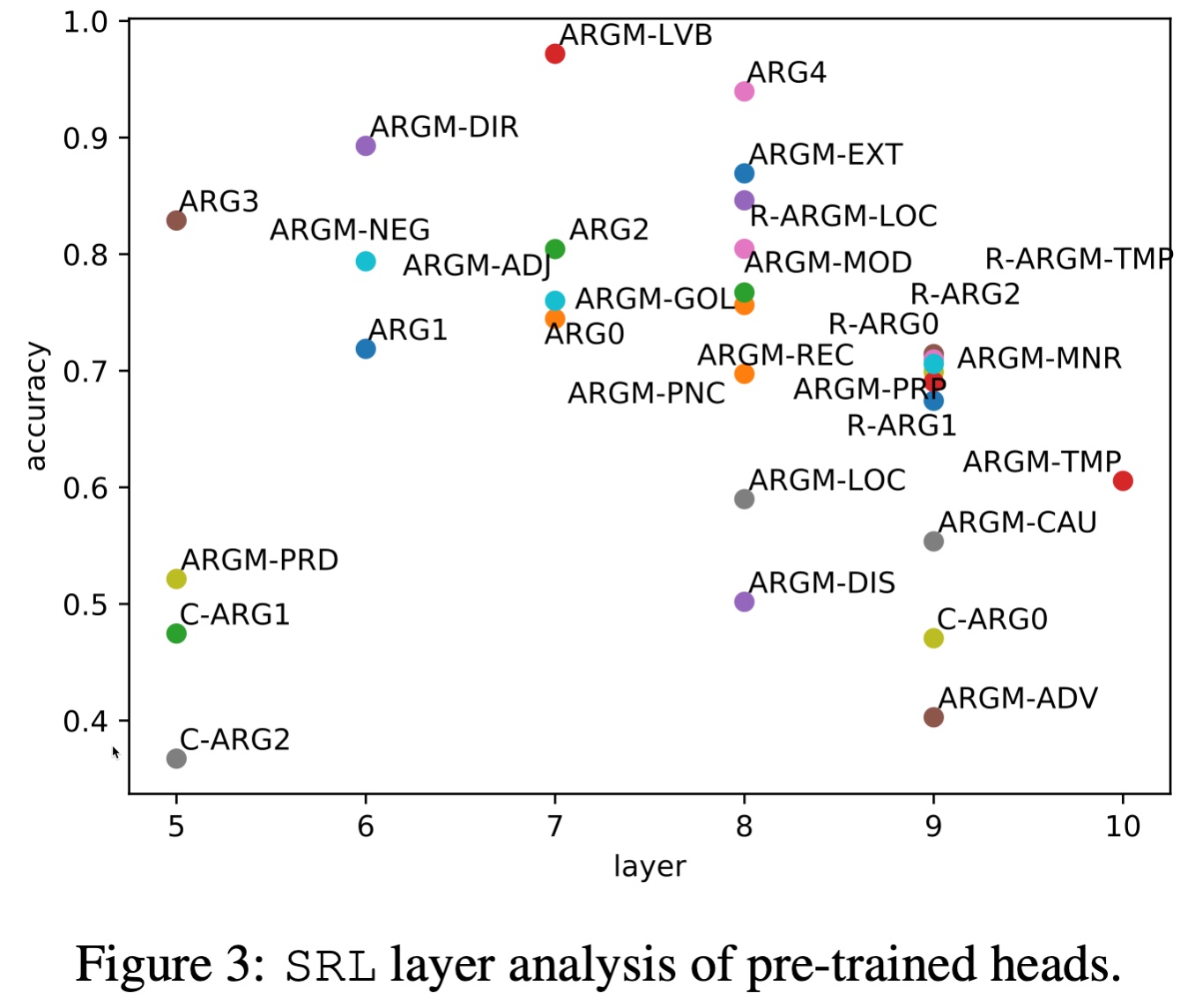
要知道每个任务涉及到多个标签,总数量是大于BERT预训练头的数量的,何况根据剪枝分析有很多注意力头用处都不大。根据鸽笼原理,注意力头必然在多种任务中都有精彩表现。这些现象说明了预训练Transformer中天才注意力头,也就是干细胞的存在。
干细胞分化
那么,这些天才注意力头在单任务和多任务学习后,发生了什么变化呢?我们发现它们大部分在单任务学习中得到了分化,但在多任务学习中却丧失了自己的专长,沦为平庸。
我们用单任务学习作为基线(红线),将每个模型每种标签(图标长度代表频率排名,越长频率越高)的准确率可视化出来后,发现几乎所有联合学习模型的大部分标签的性能都在基线以下,有些甚至低于接受监督训练之前的BERT: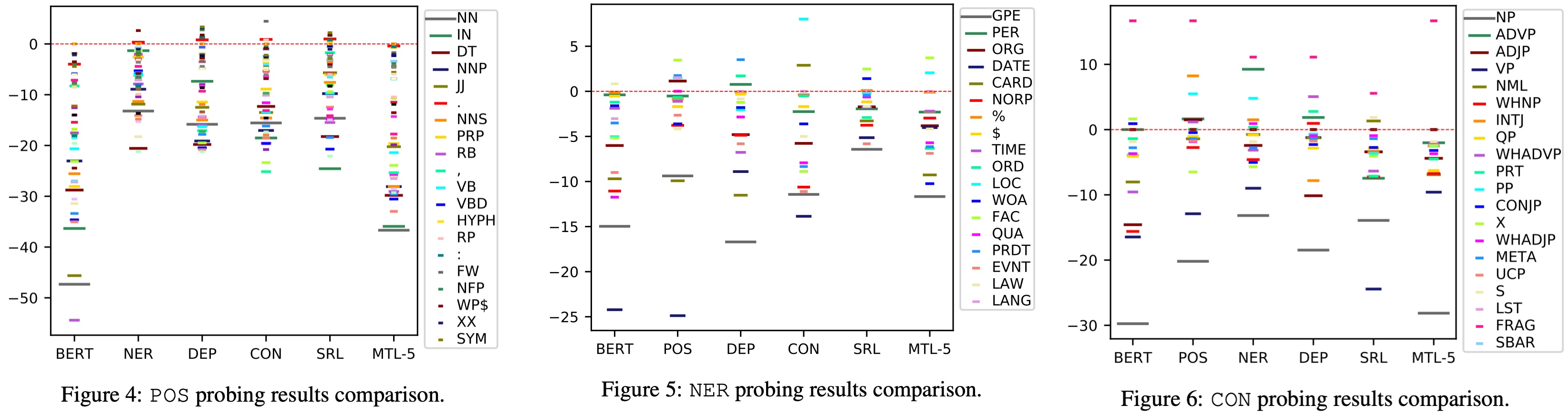
这论证了干细胞假说的第二部分:这些干细胞在多任务学习中被多个任务争夺,疲于奔命,丧失了专长。
结论
本工作分析了5个核心NLP任务之间难以调和的矛盾,发现了这些任务在争夺同一组富有天赋的注意力头。我们提出的干细胞假说认为这些注意力头类似于干细胞,能够分化为某一项任务专用,但受限于容量难以被多个任务复用。我们设计了一些新奇的探针来检测这些注意力头在训练前后的变化,结论支撑了我们的假说。
我们的假说并没有否定Transformer在多任务上的前景,而是提供了一些可能的参考方向。比如,均衡地分配注意力头,或者“克隆”干细胞等。我们的工作也存在许多局限性,比如SRL和CON探针的设计等。
 码农场
码农场