AOJ 2256 Divide the Cake 题解 《挑战程序设计竞赛》

AOJ 2256 Divide the Cake

分蛋糕：长H宽W的长方形上有2n个草莓，求在两个边上任取两点构成直线恰好将草莓平分的概率？

3.6与平面和空间打交道的计算几何 

数值积分 

开学了，近乡情更怯，好难过，刷一题缓解一下。

在左边任取一点后，作出满足条件的直线，一定有两条直线是临界情况。让这一点在自己的的邻域上下移动，另一边的有效范围变化如图：

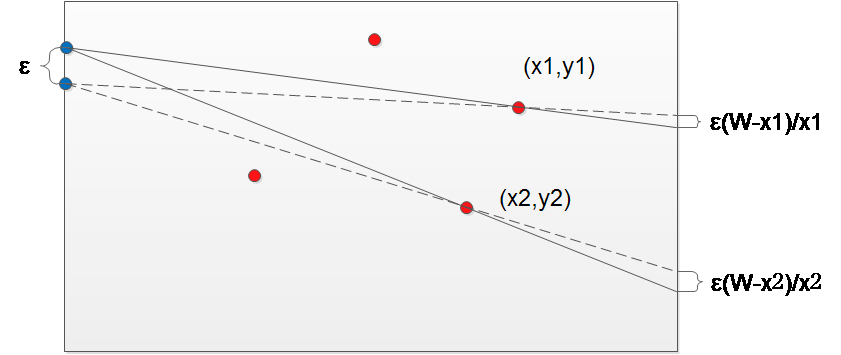
变化量为ε(W-x1)/x1 – ε(W-x2)/x2，对此积分即可。

然而并不是所有点的邻域移动都是上图的直线，对于某些点，临界情况是其他点，也就是x1,x2不同，积分表达式中的常量自然不同。

具体哪些点对应哪些临界情况，可以这么操作。任取两点构成一条直线，其在y轴上的截距相邻两两构成一个区间，该区间的点积分常量一定相同。

至于这个区间到底对应哪两个临界点，对所有直线排序后，取出极角在最中间的那两条即是。

#include <iostream>
#include <vector>
#include <complex>
#include <algorithm>
#include <cstdio>

using namespace std;

typedef complex<long double> P;

const long double EPS = 1e-10;

namespace std 
{
	bool operator <(const P &p1, const P &p2) 
	{
		if (p1.real() != p2.real()) return p1.real() < p2.real();
		return p1.imag() < p2.imag();
	}
};

// 按照y坐标排序
bool cmp(const P &p1, const P &p2) 
{
	return p1.imag() < p2.imag();
}

// 在pa和pb这两点决定的线上，横坐标为x的点的y坐标
long double calc_y_when_x_equals(const P &pa, const P &pb, long double x) 
{
	P d = pb - pa;
	if (abs(d.real()) < EPS) 
	{
		if (arg(d) < 0) return -EPS;
		else return EPS;
	}
	return pa.imag() + d.imag() * ((x - pa.real()) / d.real());
}

bool solve() 
{
	int W, H, N;
	cin >> W >> H >> N;
	if (!W && !H && !N) return false;
	N *= 2;

	vector<P> ps(N);
	for (int i = 0; i < N; ++i) 
	{
		int x, y;
		cin >> x >> y;
		ps[i] = P(x, y);
	}
	// 将四个顶点算在内的任意两点组成直线在y轴上的截距，它们相邻构成区间
	vector<P> events;
	for (int i = 0; i < N; ++i) 
	{
		for (int j = i + 1; j < N; ++j) 
		{
			events.push_back(P(0, calc_y_when_x_equals(ps[i], ps[j], 0)));
		}
		events.push_back(P(0, calc_y_when_x_equals(ps[i], P(W, 0), 0)));
		events.push_back(P(0, calc_y_when_x_equals(ps[i], P(W, H), 0)));
	}
	events.push_back(P(0, 0));
	events.push_back(P(0, H));
	sort(events.begin(), events.end(), cmp);
	// 区间收集完毕
	const int M = events.size();
	long double ans = 0;
	for (int i = 0; i < M - 1; ++i) 
	{
		const P &pa = events[i];
		const P &pb = events[i + 1];
		if (pa.imag() < 0) continue;
		if (pb.imag() > H) break;
		if (pb.imag() - pa.imag() < EPS) continue;
		const P m = (pa + pb) / (long double)2.0;
		long double upper = 0, lower = 0;
		vector<pair<long double, P>> v;
		for (const P &p : ps) 
		{
			const P d = p - m;
			v.push_back(make_pair(arg(d), p));	// 极角
		}
		sort(v.begin(), v.end());
		lower = min<long double>(H, max<long double>(0, calc_y_when_x_equals(m, v[N / 2 - 1].second, W)));	// 在右边的长度下界
		upper = min<long double>(H, max<long double>(0, calc_y_when_x_equals(m, v[N / 2].second, W)));		// 在右边的长度上界
		long double add = (pb.imag() - pa.imag()) * (upper - lower);	// 左边的长度乘以右边的长度，积分的思想
		ans += abs(add);
	}
	printf("%.10Lf\n", ans / H / H);
	return true;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	cin.tie(0);
	ios::sync_with_stdio(0);

	while (solve());
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

Reference

https://github.com/osak/Contest/blob/master/AOJ/2256.cc

 知识共享署名-非商业性使用-相同方式共享：码农场 » AOJ 2256 Divide the Cake 题解 《挑战程序设计竞赛》