码农场
公共回文子串：求两个串的公共回文子串个数。
4.7华丽地处理字符串
后缀数组
拼接后先预处理出后缀数组、高度数组和回文半径数组。其中，每个位置的回文半径用Manacher算法线性时间求出。
定义a[plen]为半径=plen的公共回文子串的个数，下面看怎么逐步求a[plen]。按照后缀字典序遍历公共子串，维护目前遇到过的包含该公共子串的回文子串。
假设回文串长度为奇数，比如例题的遍历顺序如下（后缀|公共子串|回文串）：
$CPCPC | | CPC$CPC C | | C C$CPCPC | C | C CPC | C | CPCPC CPC$CPCPC | CPC | C CPCPC | CPC | C ICPC$CPCPC | | I PC | | CPC PC$CPCPC | PC | CPC PCPC | PC | CPC
在每遇到一个长clen公共子串c的过程中，都遍历长度plen大于clen的公共回文子串p，将p的个数加到区间[clen, plen]中的每一个元素上去。因为每出现一次长plen的公共回文子串p，都代表出现了一次plen-1,plen-2, … clen的公共回文子串，示意图如下：
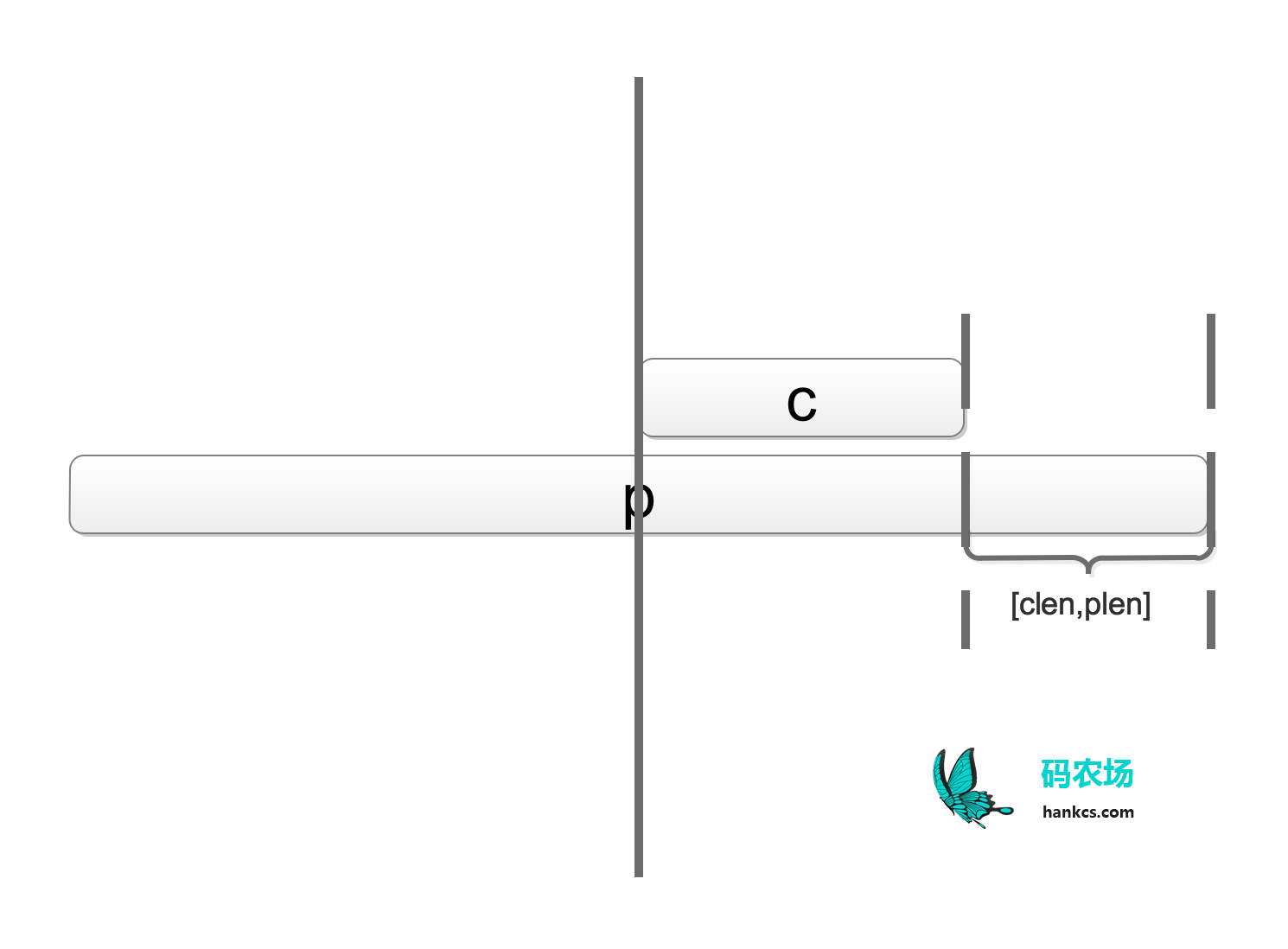
涉及到区域批量修改，所以要用BIT。
对每个位置k，都将区域和a[1,plen]累积到答案上即可。
#include <iostream>
#include <string>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long LL;
struct SA
{
static const int N = 200000; // len+1<=N
int a[N], lcp[N];
void build(const string &s)
{ build(s.c_str(), s.size()); }
void build(const char *t, int n)
{
// suffix array
static int g[N], b[N];
for (int i = 0; i < n + 1; ++i)
{
a[i] = i, g[i] = t[i];
}
b[0] = b[n] = 0;
sort(a, a + n + 1, SAComp(0, g));
for (int h = 1; b[n] != n; h *= 2)
{
SAComp comp(h, g);
sort(a, a + n + 1, comp);
for (int i = 0; i < n; ++i)
{
b[i + 1] = b[i] + comp(a[i], a[i + 1]);
}
for (int i = 0; i < n + 1; ++i)
{
g[a[i]] = b[i];
}
}
// longest common prefix (you can omit here)
for (int i = 0; i < n + 1; ++i)
{
b[a[i]] = i;
}
int h = 0;
for (int i = 0; i < n; ++i)
{
const int j = a[b[i] - 1];
while (j + h < n && i + h < n && t[j + h] == t[i + h])
h++;
lcp[b[i]] = h;
if (h)
h--;
}
lcp[0] = -1;
}
struct SAComp
{
const int h, *g;
SAComp(int h, int *g) : h(h), g(g)
{}
bool operator()(int l, int r)
{
return g[l] != g[r] ? g[l] < g[r] : g[l + h] < g[r + h];
}
};
} sa;
struct Manacher
{
static const int N = 200000 * 2; // len*2
int rad[N];
void build(const string &s)
{ build(s.c_str(), s.size()); }
void build(const char *t, int n)
{
int k;
for (int i = 0, j = 0; i < 2 * n; i += k, j = max(j - k, 0))
{
while (i - j >= 0 && i + j + 1 < 2 * n && t[(i - j) / 2] == t[(i + j + 1) / 2])
j++;
rad[i] = j;
for (k = 1; i - k >= 0 && rad[i] - k >= 0 && rad[i - k] != rad[i] - k; k++)
{
rad[i + k] = min(rad[i - k], rad[i] - k);
}
}
}
} mana;
struct BIT
{
static const int N = 80000;
LL x[N];
void init()
{ memset(x, 0, sizeof(x)); }
void add(int k, LL a)
{
for (; k < N; k |= k + 1)
x[k] += a;
}
LL sum(int k)
{
LL s = 0;
for (; k >= 0; k = (k & (k + 1)) - 1)
s += x[k];
return s;
}
LL rsum(int i, int j)
{ return i == 0 ? sum(j) : sum(j) - sum(i - 1); }
LL esum(int i)
{ return rsum(i, N - 1); }
} sum[2], cnt[2];
int of[200000];
int main()
{
string S, T;
cin >> S >> T;
const string F(S + '$' + T);
sa.build(F);
mana.build(F);
for (int i = 0; i < F.size() + 1; ++i)
{
of[i] = sa.a[i] > (int) S.size();
}
LL ans = 0;
for (int odd = 0; odd < 2; ++odd)// 回文长度是否为奇数
{
for (int i = 0; i < 2; ++i)
sum[i].init(), cnt[i].init();
map<int, int> palindrome[2];// AB各自的回文子串半径plen的个数
for (int k = 1; k < (int) F.size() + 1; k++)
{
const int clen = sa.lcp[k];// 公共子串的长度
for (int i = 0; i < 2; ++i)
{
map<int, int>::iterator it = palindrome[i].lower_bound(clen + 1);
while (it != palindrome[i].end())// 遍历半径大于公共子串clen的回文子串
{//维护Binary Indexed Tree
const int plen = it->first, p = it->second;// 回文子串长度及个数
sum[i].add(plen, -(LL) plen * p);//在[clen,plen]区间同时加上p
cnt[i].add(plen, -p);
sum[i].add(clen, (LL) clen * p);
cnt[i].add(clen, p);
palindrome[i][clen] += p;
palindrome[i].erase(it++);
}
}// 在sa[k]位置的回文半径
const int plen = odd ? mana.rad[sa.a[k] * 2] / 2 + 1 : sa.a[k] ? mana.rad[sa.a[k] * 2 - 1] / 2 : 0;
ans += sum[1 - of[k]].sum(plen) + (LL) plen * cnt[1 - of[k]].esum(plen + 1);//前plen项之和
sum[of[k]].add(plen, plen); // a[plen] += 1
cnt[of[k]].add(plen, 1);
palindrome[of[k]][plen]++;
}
}
cout << ans << endl;
return 0;
}
Reference
http://d.hatena.ne.jp/kohyatoh/
知识共享署名-非商业性使用-相同方式共享：码农场 » AOJ 2292 Common Palindromes 题解《挑战程序设计竞赛》