imos-累积和法

在解AOJ 0531 Paint Color时，学到了一个累积和的妙用——imos法，由于原文是日语，所以特意翻译过来。值得一提的是，作者Kentaro Imajo跟鄙人同龄，却已取得如此多的成就，而鄙人一无所成，实在汗颜。

imos法

imos法是将累积和算法拓展到多次元、高次空间的方法。虽然程序竞赛中出题最多不过2次元1次，但是2012年Kentaro Imajo将其用于高次元高次空间，在信号处理/图像处理领域取得了成就。

基础imos法

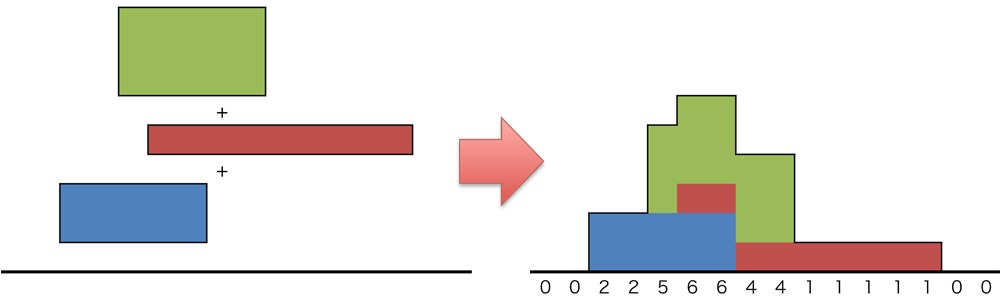
最简单的imos法是1次元0次系数的求解思想。如图，有三个俄罗斯方块在一起，悬空的部分会掉下去，求从左到右的高度？这个高度就是横坐标固定时，上面矩形高度之和。这就是最简单的imos法。

例题

你在经营一个咖啡厅，你的咖啡厅里每个客人在S_i时刻进店，E_i时刻出店。求店里最多有多少客人？（客人最多C个，时刻在T内。如果有多人同时进店出店，先算出店的人）。

朴素的解法

朴素的思想是，计算每个时刻客户的数量，从中找出最大值。但是，复杂度是O(CT)

#include <iostream>
#include <algorithm>
using namespace std;

#define C 4
#define T 10
// 每个客人的进入时间
int S[C] = { 1, 3, 5, 7 };
// 每个客人的离开时间
int E[C] = { 2, 8, 6, 8 };
// 店里的人数
int table[T];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	memset(table, 0, sizeof(table));
	for (int i = 0; i < C; i++) 
	{
		// 从时间 S[i] 到 E[i] - 1 店里人数计数加一
		for (int j = S[i]; j < E[i]; j++) 
		{
			table[j]++;
		}
	}
	// 找最大値
	cout << *max_element(table, table + T) << endl;
	system("pause");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

imos法解法

imos法的基本方向是，只统计出入店时刻的人数变化（我个人理解相当于求导），入店+1，出店-1。最终统计的时候，需要将每个时刻加上前一个时刻的统计量（我个人理解相当于求积分），其中的最大值就是所求。记录复杂度O(C)，累加复杂度O(T)，所以整体复杂度O(C+T)。

#include <iostream>
#include <algorithm>
using namespace std;

#define C 4
#define T 10
// 每个客人的进入时间
int S[C] = { 1, 3, 5, 7 };
// 每个客人的离开时间
int E[C] = { 2, 8, 6, 8 };
// 店里的人数
int table[T];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	memset(table, 0, sizeof(table));
	for (int i = 0; i < C; i++) 
	{
		table[S[i]]++;  // 入店+1
		table[E[i]]--;  // 出店-1
	}
	// 累加
	for (int i = 1; i < T; i++) 
	{
		table[i] += table[i - 1];
	}
	// 找最大値
	cout << *max_element(table, table + T) << endl;
	system("pause");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

推广到二次元

imos相对于朴素方法的一个优点就是随着次元增大复杂度的降低越明显。

例题

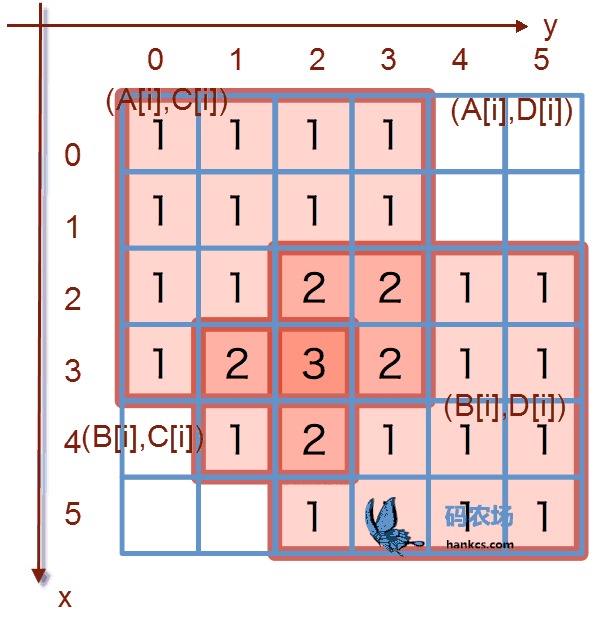
你在玩一个抓怪兽的游戏，现在你面前是一张W*H的地图，地图里有N种怪物。怪物i只会在左下角为（B_i,C_i），右上角为(A_i,D_i)的矩形区域内出现。求单位区域内最多有多少种怪兽？

朴素解法

朴素的解法就是计算每一个单位区域内出现的怪兽数，然后找出最大值。复杂度是O（NWH）。

#include <iostream>
#include <algorithm>
using namespace std;
#define  W  6
#define  H  6
#define  N  4
// 左下角坐标
int B[N] = {3,4,3,5,};
int C[N] = {0,1,2,2,};
// 右上角坐标
int A[N] = {0,3,2,2,};
int D[N] = {3,2,3,5,};
// 地图上的分布结果
int tiles[H][W];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	memset(tiles, 0, sizeof(tiles));
	for (int i = 0; i < N; i++) 
	{
		// 怪兽 i 出现的范围 [(A[i],C[i]), (B[i],D[i])) 内的计数加一
		for (int y = C[i]; y < D[i]; y++) 
		{
			for (int x = A[i]; x < B[i]; x++) 
			{
				tiles[y][x]++;
			}
		}
	}
	// 求最大値
	cout << *max_element(tiles[0], tiles[0] + H * W) << endl;
	system("pause");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

imos法解法

矩形的左上角 (A[i],C[i])  +1 ，右上角 (A[i],D[i]) −1，左下角 (B[i],C[i])  −1 ，右下角(B[i],D[i]) +1 ，统计最终结果之前累加。加一减一 O(N)，累加(WH) 整体复杂度 O(N+WH) 。

#include <iostream>
#include <algorithm>
using namespace std;
#define  W  6
#define  H  6
#define  N  4
// 左下角坐标
int B[N] = {3,4,3,5,};
int C[N] = {0,1,2,2,};
// 右上角坐标
int A[N] = {0,3,2,2,};
int D[N] = {3,2,3,5,};
// 地图上的分布结果
int tiles[H][W];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	memset(tiles, 0, sizeof(tiles));
	// 影响力计算 (图 3)
	for (int i = 0; i < N; i++) 
	{
		tiles[C[i]][A[i]]++;
		tiles[C[i]][B[i]]--;
		tiles[D[i]][A[i]]--;
		tiles[D[i]][B[i]]++;
	}
	// 横向累积和 (图 4, 5)
	for (int y = 0; y < H; y++) 
	{
		for (int x = 1; x < W; x++) 
		{
			tiles[y][x] += tiles[y][x - 1];
		}
	}
	// 纵向累积和 (图 6, 7)
	for (int y = 1; y < H; y++) 
	{
		for (int x = 0; x < W; x++) 
		{
			tiles[y][x] += tiles[y - 1][x];
		}
	}

	cout << *max_element(tiles[0], tiles[0] + H * W) << endl;
	system("pause");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

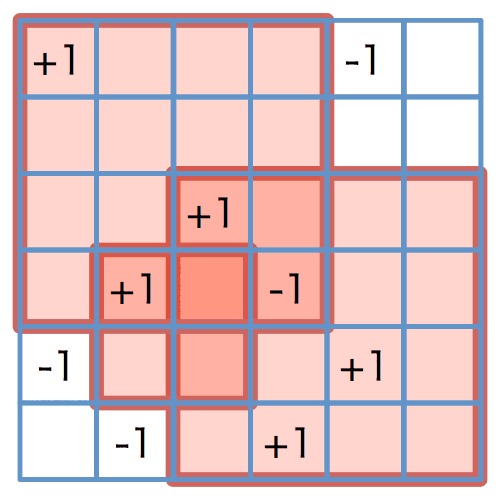
图三：影响力计算

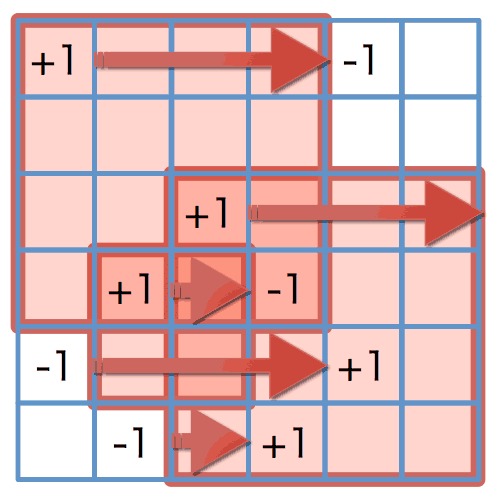
图四：横向累加

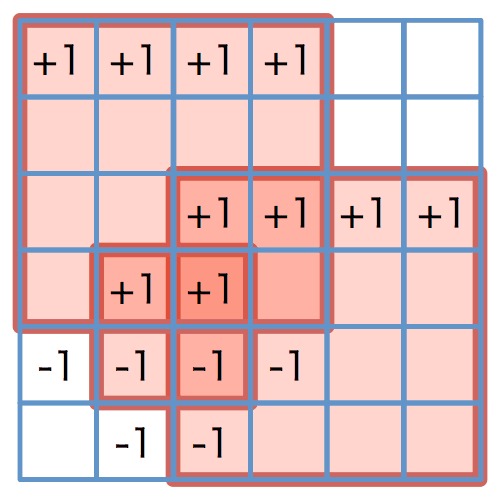
图五：横向累加结果

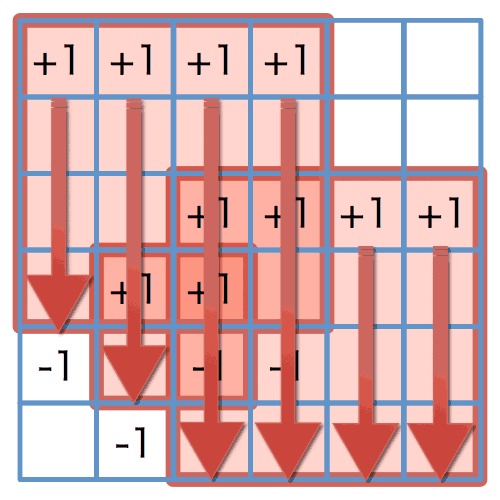
图六：纵向累加

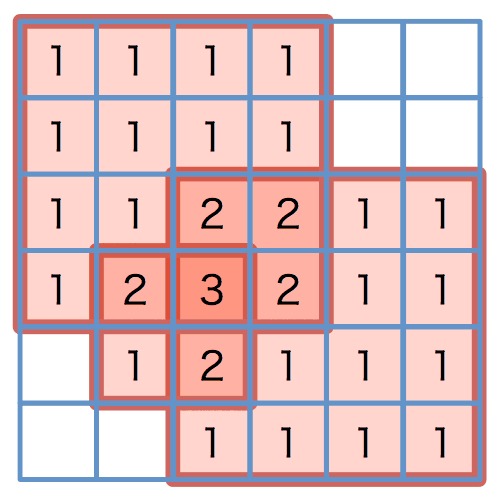
图七：纵向累加结果

更高级的用法

暂时用不到，记录一个地址，有空再看。

Reference

http://imoz.jp/algorithms/imos_method.html

 知识共享署名-非商业性使用-相同方式共享：码农场 » imos-累积和法