![]()

某组合电路有N个输入,M个与或异或门将其两两相连构成多个输出,问是否存在满足给定输出的输入。
4.3成为图论大师之路
2-SAT
每条边都是某个2输入门,最终输出为门的合取范式,典型的2-SAT问题。
根据蕴涵门的定义:
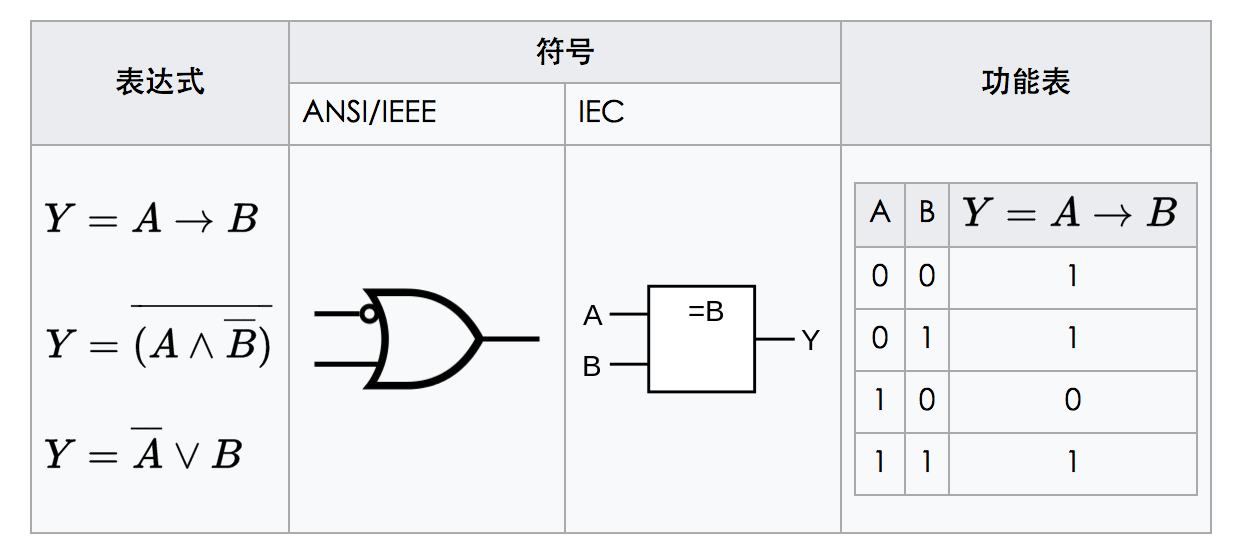
将与或异或门写成等价的蕴涵门形式:
| A AND B = 1 | !A->A | !B->B | ||
| A AND B = 0 | A->!B | B->!A | ||
| A OR B = 1 | !A->B | !B->A | ||
| A OR B = 0 | A->!A | B->!B | ||
| A XOR B = 1 | A->!B | !B->A | !A->B | B->!A |
| A XOR B = 0 | A->B | B->A | !A->!B | !B->!A |
表格中的蕴涵表达式之间的运算符为与,证明很简单,利用A->B = !A OR B进行布尔运算,或者干脆列个真值表也行。
然后就是利用强连通分量分解了,节点i表示x的话,i+N表示!x。
跑完scc后,检查i与i+N是否在同一个强连通分量中,如果是,显然无解。
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define MAX_V 10000
int V; // 顶点数
vector<int> G[MAX_V]; // 图的邻接表表示
vector<int> rG[MAX_V]; // 反向图
vector<int> vs; // 后序遍历顺序的顶点列表
bool used[MAX_V]; // 访问标记
int cmp[MAX_V]; // 所属强连通分量的拓补序
void add_edge(const int &from, const int &to)
{
G[from].push_back(to);
rG[to].push_back(from);
}
void dfs(const int &v)
{
used[v] = true;
for (int i = 0; i < G[v].size(); ++i)
{
if (!used[G[v][i]])
dfs(G[v][i]);
}
vs.push_back(v);
}
void rdfs(const int &v, const int &k)
{
used[v] = true;
cmp[v] = k;
for (int i = 0; i < rG[v].size(); ++i)
{
if (!used[rG[v][i]])
rdfs(rG[v][i], k);
}
}
int scc()
{
memset(used, 0, sizeof(used));
vs.clear();
for (int v = 0; v < V; ++v)
{
if (!used[v])
dfs(v);
}
memset(used, 0, sizeof(used));
int k = 0;
for (int i = vs.size() - 1; i >= 0; --i)
{
if (!used[vs[i]])
rdfs(vs[i], k++);
}
return k;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
int M, N;
scanf("%d%d", &N, &M);
V = 2 * N;
for (int i = 0; i < M; ++i)
{
int a, b, c;
char buf[10];
scanf("%d%d%d %s", &a, &b, &c, buf);
if (buf[0] == 'A')
{
if (c == 1)
{
add_edge(a + N, a);
add_edge(b + N, b);
}
else
{
add_edge(a, b + N);
add_edge(b, a + N);
}
}
else if (buf[0] == 'O')
{
if (c == 1)
{
add_edge(a + N, b);
add_edge(b + N, a);
}
else
{
add_edge(a, a + N);
add_edge(b, b + N);
}
}
else if (buf[0] == 'X')
{
if (c == 1)
{
add_edge(a + N, b);
add_edge(a, b + N);
add_edge(b + N, a);
add_edge(b, a + N);
}
else
{
add_edge(a + N, b + N);
add_edge(a, b);
add_edge(b + N, a + N);
add_edge(b, a);
}
}
}
scc();
bool yes = true;
for (int i = 0; i < N; ++i)
{
if (cmp[i] == cmp[i + N])
{
yes = false;
break;
}
}
puts(yes ? "YES" : "NO");
#ifndef ONLINE_JUDGE
fclose(stdin);
#endif
return 0;
}
| 16429721 | hankcs | 3678 | Accepted | 824K | 172MS | C++ | 2687B | 2016-12-28 14:26:38 |
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3678 Katu Puzzle 题解《挑战程序设计竞赛》
知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3678 Katu Puzzle 题解《挑战程序设计竞赛》
 码农场
码农场