目录
AC自动机中,转移的最小单位是一个字符。也就是说,匹配后只能移动一个字符,复杂度是线性的$O(n)$。然而线性并非最快,Boyer-Moore算法在匹配后可以跳过多个字符,比线性还快。据说在实践中,利用Boyer-Moore优化的AC自动机总是更快。
来熟悉一下Boyer-Moore算法的基本思路。假设模式串的长度为$m$,母文本为$t$。算法不是去母文本中找模式串,而是在模式串中从右到左找文本的第 $m$个字符$t_m$。如果没找到,那么就可以在母文本中跳过$m$个字符,继续搜索$t_{2m}$。如果找到了,比如说是模式串的第$2$个字符,那就可以跳过$m-2$个字符,继续搜索$t_{2m-2}$,以此类推。$t_i$恰好与模式串尾部匹配的时候,再比较剩下的$t_{i-1} \cdots t_{t-m}$,直到这$m$个字符都匹配上。该算法可利用下图演示(二进制串匹配,白色代表$0$,绿色代表$1$):
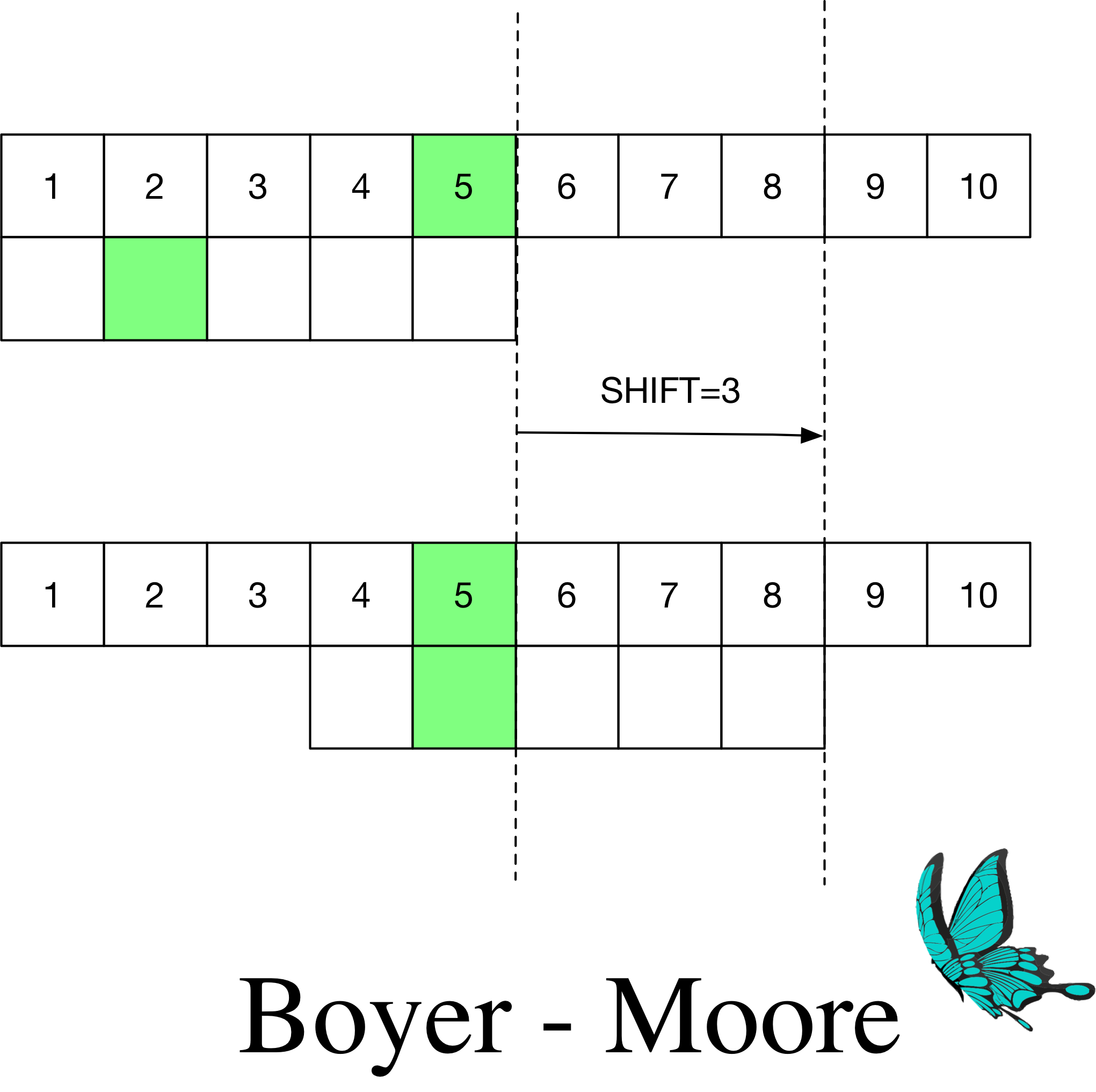
上例在匹配下标$5$后直接快进了$3$个字符。
Wu Manber利用了Boyer-Moore的思路,将该算法拓展到多模式匹配。
预处理
第一步要算出所有模式串上的最小长度$m$,然后先考虑每个模式串的前$m$个字符。如此所有模式串长度都一样了。注意如果最短模式串非常短,比如长度为$1$,则算法不可能跳过$2$及以上个字符,效率变低。
如果每次比较不局限于$1$个字符,而是比较$B$个字符,则比较次数可以减小到$\frac{1}{B}$。同时每次在模式串位置$i$匹配上了之后可以跳过的字符数减小到$m-i-B+1$,都不匹配时$i=0$。
SHIFT表的构造
用一个SHIFT表储存匹配后最大可以跳过的字符数,将每个长$B$的“子串”哈希到一个整数,对应SHIFT表中的下标。那么SHIFT表的大小理论上是$\Vert \Sigma\Vert^B$,其中$\Sigma$是字符表。
SHIFT表还可以理解为,后缀作为子串在模式串中离尾部的最短距离(上图为$3$)。
记正在扫描的$B$个字符为$X=x_1 \cdots x_B$,并且$X$被哈希到$i$,在所有模式串从右到左寻找$X$,则会发生两种情况:
-
所有模式串都不含$X$
此时可以跳过$m-B+1$,将其存入SHIFT[i]中。 -
存在包含$X$的模式串
找到$X$在这些模式串中的下标中的最大值(也即最右位置)$q$,将$m-q$存入SHIFT[i]。
为了得到这样的SHIFT表,只需枚举所有模式串(的前$m$个字符)中长$B$的子串$a_{j-B+1}\cdots a_j$,将$m-B+1$(子串位于模式串首部之外,即不含该子串)和$m-j$(子串位于模式串的下标$j$处)中的较小者存入SHIFT表即可。这个值代表最少需要移动多少个字符来“对齐”这个子串,大于这个值的话会遗漏某些模式串,小于等于这个值则是安全的。
SHIFT表的压缩
考虑到SHIFT表可能很大,现在看看如何压缩。SHIFT表的定义是匹配子串时最大可以跳过的字符数,如果这个值比精确值大,算法会出错;然而小一点则不会出错,只会降低效率。于是可以将一些子串放到同一个下标中,只需将SHIFT值设为它们的SHIFT值的最小值。实践中在模式串很少的时候,使用$B=2$、精确形式;在模式串很多的时候使用$B=3$、压缩形式。
HASH表的构造
在$SHIFT[h]=0$的时候(尾部$B$个字符匹配成功,不应该跳过,也就是说匹配到了公共后缀)需要找到那些以该子串结尾的模式串,复用SHIFT表的哈希函数,制作另一张HASH表,值为以该子串结尾的所有模式串。HASH表比SHIFT表稀疏(因为只储存后缀),可以考虑只利用哈希值最后几个比特得到更紧凑的结构。
记$h$为哈希函数的输出值,将所有模式串按后缀的哈希排序,那么必然有一些连续区域的哈希值是相同的,也就是说这些区域共享长$B$的后缀。将排序后的模式串记录为链表,其中的指针记为$p$。那么HASH表格就是以索引连续区域(子链表)为目标构造的结构。
$SHIFT[h]=0$时,此时$HASH[h]$指向一个子链表的首部$p$,不断递增$p$直到$p+1$等于$HASH[h+1]$时即可得到子链表的尾部元素。
PREFIX表的构造
由于自然语言中的单词经常共享后缀,比如ion或ing。这会导致HASH表中索引的模式串分布非常不均匀,产生大量冲突。极端情况下可能所有模式串都被映射到同一条目中。此时必须对所有模式串逐一比对,降低了效率。为了解决这个问题,引入了另一个PREFIX表。
在上一节中HASH表维护的是长$B$的后缀,类似地PREFIX维护的长$B^\prime$的前缀。HASH表除了索引模式串本身外,还索引了模式串长$B^\prime$的前缀的哈希值。在母文本与模式串的后缀匹配的情况下,先用HASH表得到所有后缀相同的模式串,然后用母文本长$m$的窗口移动$m-B^\prime$得到前缀,去PREFIX表得到哈希值,用这个哈希值过滤一下,剩下的就是需要逐一匹配的模式串。
事实上PREFIX表不是算法必须的,特别是在一些公共后缀不多的情况下。PREFIX表其实也不是一张Key-Value表,只是一个哈希函数而已,记作PREFIX(x)。
匹配
其实匹配的过程在预处理环节已经提到不少,正是因为匹配时要用到,所以才需要这3个表格的预处理。归纳起来,匹配过程的主循环可以描述为如下4步:
-
计算母文本中当前长$B$的后缀$t_{m-B+1} \cdots t_m$的哈希值$h$。
-
检查SHIFT[h]:如果$> 0$则跳过SHIFT[h]个字符并转到1;否则,转到3。
-
计算当前位置往左$m$的长$B^\prime$的前缀的哈希值,记为text_prefix_hash
-
检查$HASH[h]\leq p < HASH[h+1]$区间内的p是否有PREFIX(p)=text_prefix_hash,当两者相等时,进一步直接比较模式串与这段来自母文本的子串。当它们完全匹配的时候,就找到了一个模式串。无论找到与否,都将当前位置右移1个字符,并跳转1。
Oh et al. (2014)举了个例子:
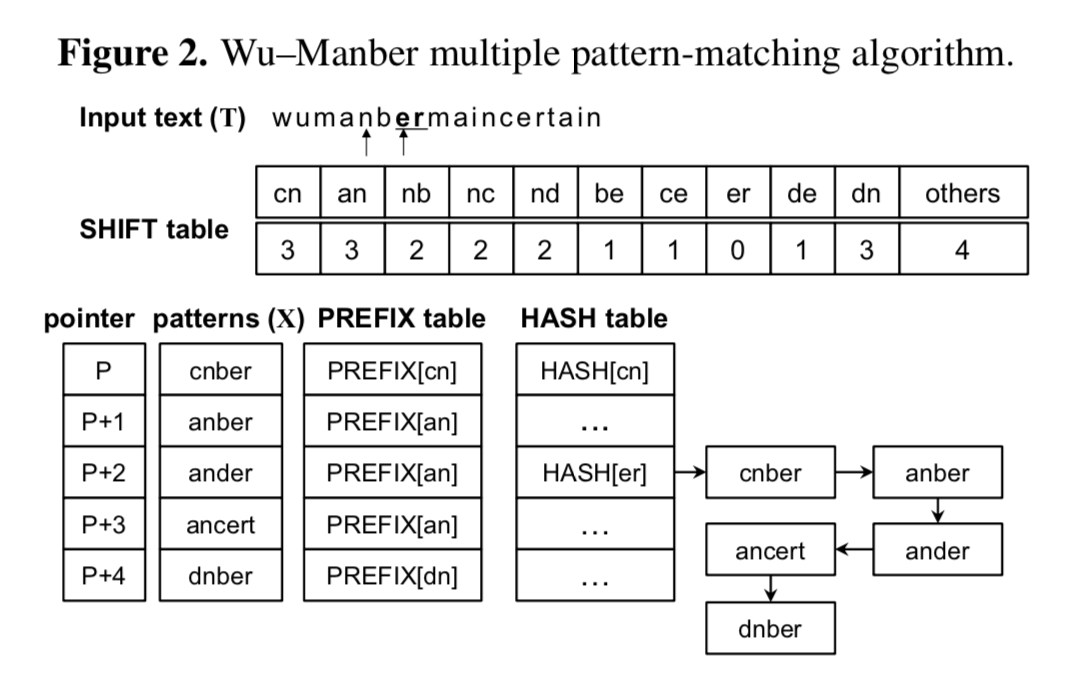
这里$m=5,B=B^\prime=2$,当前正在匹配的后缀是nb,前缀是um。由于在所有模式串中,nb离尾部的距离最小为$2$,所以SHIFT[nb]=$2$,跳过$2$个字符;此时后缀变为er,前缀变为an。后缀er的SHIFT值为0,检查一下HASH表中具有公共前缀的模式串{anber, ander, ancert},发现anber完全匹配。输出anber后,当前位置移动$1$个字符,跳转$1$。
事实上,在后缀匹配成功后,总是只能跳$1$个单位,依然不够快。另外,HASH表已经够费内存的了,额外再加一个PREFIX表,双倍内存。
复杂度
$P$个模式串,$M=mP$是所有模式串的总长度,最多$P=M/m$个子串对应同一个SHIFT值$i$(极端情况下所有模式串在位置$i$的子串都相等)。长$B$的子串最少有$M$个(极端情况下$B=1$,所有模式串长度都为$1$。这是我的理解,与论文给出的$2M$不同,我举出的反例如上所述)。所以随机挑一个子串,它的SHIFT值为某个特定值$i$的概率小于两者之比$1/m$。
哈希函数的复杂度是$O(B)$,母文本长度$N$,不跳转的情况下($i=0$)复杂度为三者乘积$O(BN/m)$;跳转的情况下,平均SHIFT值为$\frac{1+\cdots + m-B+1}{m}=O(\frac{m}{2})$,复杂度为哈希复杂度乘以文本长度除以平均SHIFT值,也是$O(BN/m)$。所以Wu Manber是总体复杂度就是$O(BN/m)$。
变种
为了解决$SHIFT[i]=0$时无法跳过更多字符的问题,Oh et al. (2014)提出对所有这样的后缀额外记录一个SHIFT值,代表该后缀第$2$小的SHIFT值,称为auxiliary shift(ASHIFT)。匹配成功后按ASHIFT快进。
为什么可以跳过这么多呢?因为$SHIFT[i]$的定义保证了所有模式串在跳过的区间内不会含有该后缀$i$。当$SHIFT[i]=0$时,最短距离为$0$已经考虑了,接着跳过所有模式串中$i$离尾部的第二短距离,当然是安全的。
ASHIFT表的构造
在构造SHIFT表的过程中,当新的$SHIFT[i]=0$时,如果$ASHIFT[i] \neq NULL$,用旧的$SHIFT[i]$和$ASHIFT[i]$中的较小者更新$ASHIFT[i]$。如果说$SHIFT[i]$储存的是后缀作为模式串的子串离尾部的最短距离的话,$ASHIFT[i]$储存的就是第二短的距离。这个过程可以用下面两张图描述:
$m=5, B=1$,一共两个模式串。
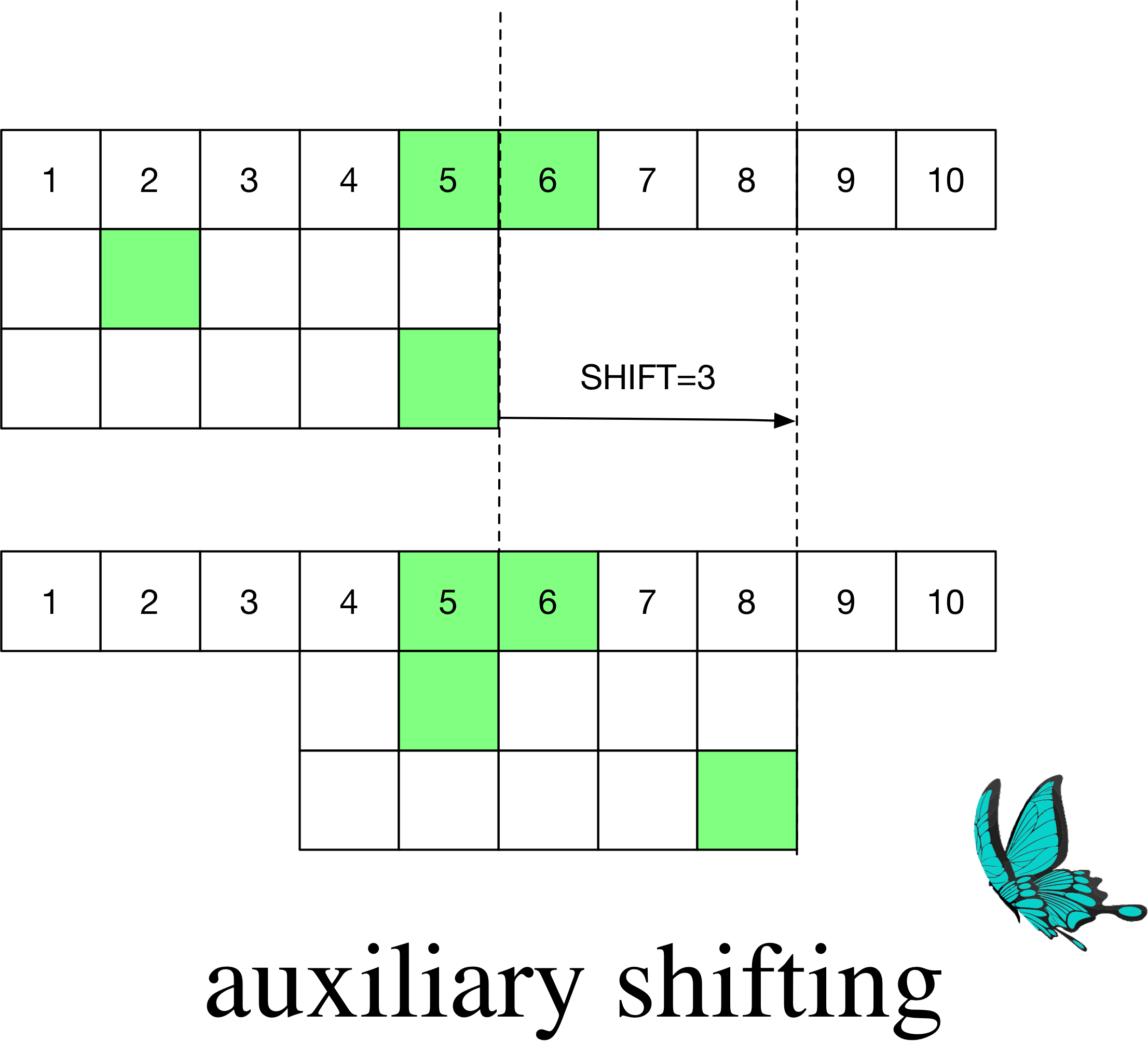
此时第二短的距离是$3$,来自第一个模式串。
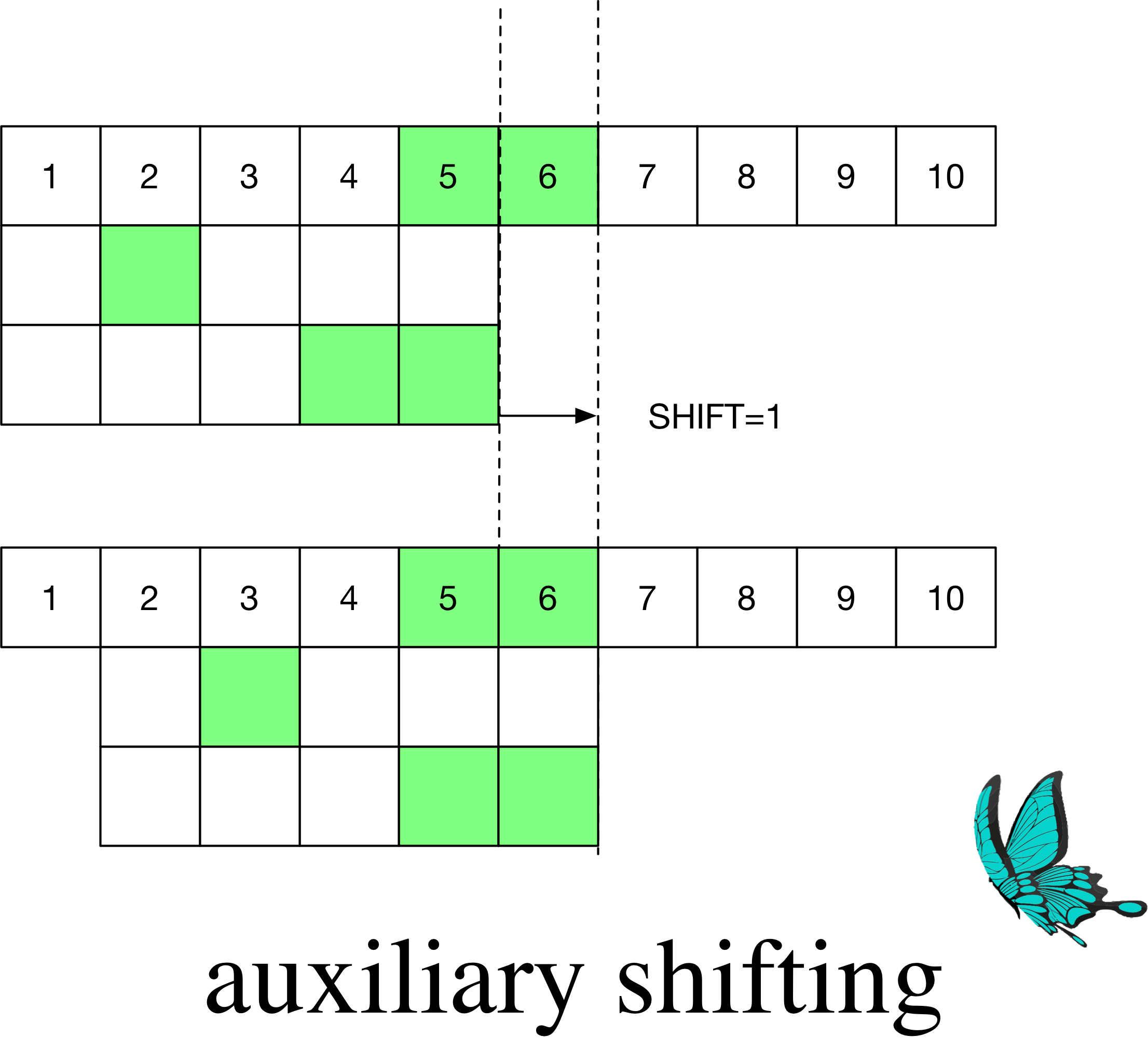
此时第二短的距离是$1$,来自第二个模式串(最短距离来自相同的模式串)。
回过头来看对上一个例子的加速,由于所有模式串的前$5$个字符都以$er$结尾,所以$ASHIFT[er]=m-B+1=4$:
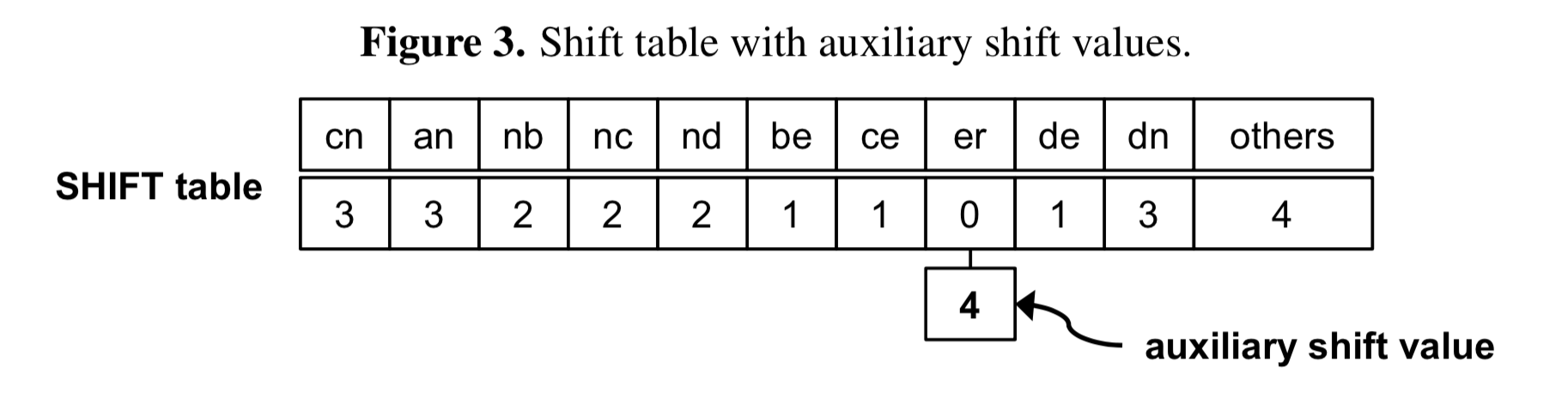
在匹配了er之后不再只跳过$1$,而是可以安全地跳过$4$个字符:

Early Decision Method
在步骤4检查$HASH[h]\leq p < HASH[h+1]$区间内的p是否有PREFIX(p)=text_prefix_hash时,可以通过预先排序PREFIX(p)。检索有序列表比无序列表快。即使后缀和前缀都匹配上了,剩下的片段也可以预先排序。有序列表上的顺序检索可以early stopping。
总结
Wu Manber算法理论上复杂度为$O(BN/m)$($1 \leq B \leq m = min(strlen(M))$),与AC自动机的$O(N)$相比,只有在特定条件下($B \ll m$)才能体现出优势。这个特定条件很苛刻,要求模式串不能太短。而在自然语言处理的场景下,经常有单字作为模式串的情况,此时Wu Manber无法跳过多个字符,没有优势。另外,汉语最常见的词语长度为$2$,也限制了该算法的使用。
另一方面,Wu Manber所依赖的哈希表则带来了很大的内存负担,如果哈希函数复杂度本身很高,更加得不偿失。
题外话,算法研究没有止境,再简单的问题,也有一条历史悠久的进化路线与错综复杂的变种。
References
Wu S, Manber U. A fast algorithm for multi-pattern searching[J]. 1994.
D. Oh, D. Kim, and W. Ro, “A Malicious Pattern Detection Engine for Embedded Security Systems in the Internet of Things,” Sensors, vol. 14, no. 12, pp. 24188–24211, Dec. 2014.
V. Bhardwaj and V. Garg, “A Comparative Study of Wu Manber String Matching Algorithm and its Variations,” International Journal of Computer Applications, vol. 132, no. 17, pp. 34–38, Dec. 2015.
 码农场
码农场
我的解决方法是将一个字的模式提取出来放到另外的组中使用单独的算法,其余的模式在一组中使用 这个算法。然后统一在外面包装一下,对使用者透明,效果不错。
大牛啊 持续关注