最小生成树算法初步-码农场

最小生成树Prim算法
Prim算法的实现
最小生成树Kruskal算法
最小生成树Kruskal算法的实现

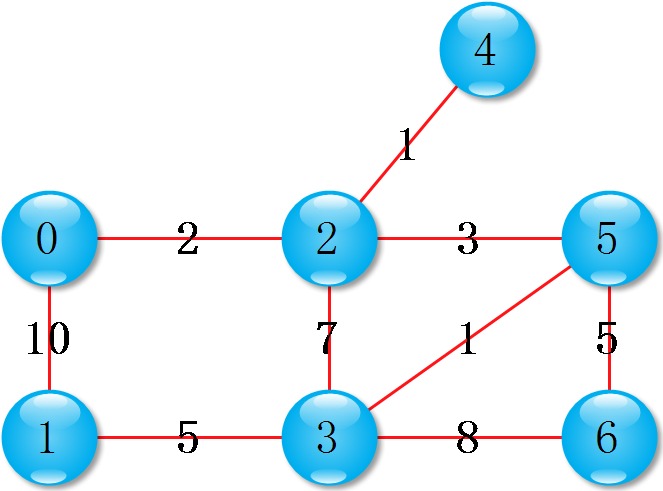
最小生成树Prim算法

与Dijkstra算法类似，任意挑一个顶点，添加最短边，直至所有顶点都在树中，此时就得到一颗最小生成树了。

证明：

令V为顶点集合，已求得顶点集合为X，V上的最小生成树为T。

假设连接X和V\X的最短边为e，现在需要证明T包含e。

如果T不包含e的话，将e加入T形成一个圈（e是圈的一条边），那么e的两个端点X和V\X之间必定还有一条边f，且f权重比e大，假如删掉f，此时的树成了一颗比最小生成树还小的树，形成矛盾。

Prim算法伪码

MST-PRIM(G, w, r)

1 for each u ∈ G.V

2       u.key ← ∞

3       u.π ← NIL

4   r.key ← 0

5   Q ← G.V

6   while Q ≠ Ø

7       u ← EXTRACT-MIN(Q)

8       for each v ∈ G.Adj[u]

9           if v ∈ Q and w(u, v) < v.key

10              v.π ← u

11              v.key ← w(u, v)

Prim算法复杂度分析

使用最小堆实现Q的话，

第5行构造最小堆耗时O(V)。
然后EXTRACT-MIN(Q)=O(log V)，一共调用V次，所以第6和7行复杂度为O(VlogV)。
第8行一共调用2E次（无环图），每次的内层循环复杂度多少呢？第11行修改了最小堆中的一个元素，这个元素需要调整自己的位置，这在最小堆中的代价是O(log V)。

最终复杂度为O(V+VlogV+ElogV)=O(ElogV)。

使用FIBONACCI实现Q的话，

相同
相同
依然调用2E次，但每次复杂度O(1)

最终复杂度为O(V+VlogV+E)=O(E+VlogV)。

为什么我们在上面的最终计算中都忽略了V？因为E的大小是V的平方。

Prim算法的实现

记链接X和V的边的最小权值为mincost[v]，添加新顶点u的时候，只需更新u相连的顶点的最小权值即可。

mincost[v] = min(mincost[v] , weight(u, v))。

如果直接遍历mincost找出最小值的话，复杂度为O(|V|²)，使用最小堆的话复杂度降低为O(|E|log|V|)。

#include <iostream>
#include <queue>
#include <functional>
using namespace std;
#define MAX_V 1024

int mincost[MAX_V];		// 从集合X出发的边到每个顶点的最小权值
bool used[MAX_V];		// 顶点i是否包含在集合X中
int V;					// 顶点数
// first 最短路径，second顶点编号
typedef pair<int, int> P;
struct edge
{
	int to, cost;
	edge(int to = 0, int cost = 0) : cost(cost), to(to) {}
};
// 边
vector<edge> G[MAX_V];	// G[i] 顶点i到G[i].to的权值为G[i].cost

int prim()
{
	int res = 0;
	memset(mincost, 0x3f, V * sizeof(int));
	memset(used, 0, V * sizeof(bool));
	mincost[0] = 0;
	priority_queue<P, vector<P>, greater<P> > que;
	que.push(P(0, 0));  
	while (!que.empty())
	{
		P p = que.top(); que.pop();
		int v = p.second;  
		if (used[v] || p.first > mincost[v]) continue;
		used[v] = true;
		res += mincost[v];
		for (int i = 0; i < G[v].size(); ++i)
		{
			edge e = G[v][i];
			if (mincost[e.to] > e.cost)
			{
				mincost[e.to] = e.cost;
				que.push(P(mincost[e.to], e.to));
			}
		}
	}
	return res;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	// 测试数据
	V = 7;
	G[0].push_back(edge(1, 10));
	G[1].push_back(edge(0, 10));
	G[0].push_back(edge(2, 2));
	G[2].push_back(edge(0, 2));
	G[1].push_back(edge(3, 5));
	G[3].push_back(edge(1, 5));
	G[2].push_back(edge(3, 7));
	G[3].push_back(edge(2, 7));
	G[2].push_back(edge(4, 1));
	G[4].push_back(edge(2, 1));
	G[2].push_back(edge(5, 3));
	G[5].push_back(edge(2, 3));
	G[3].push_back(edge(5, 1));
	G[5].push_back(edge(3, 1));
	G[3].push_back(edge(6, 8));
	G[6].push_back(edge(3, 8));
	G[5].push_back(edge(6, 5));
	G[6].push_back(edge(5, 5));
	cout << prim() << endl;
	system("pause");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

最小生成树Kruskal算法

按照边的权值从小到大尝试加入最小树，如果不产生圈就加进去，否则就扔掉。

关于判断是否产生圈，可以利用并查集来高效地实现。连通的顶点放入一个并查集（连通分量）里，如果一条边e的两个顶点u, v不在同一个连通分量中，那么将e加进来也不会产生圈。

最小生成树Kruskal算法的实现

#pragma warning(disable : 4996)
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX_E 1024

// 并查集相关数据与算法
#define MAX_N MAX_E + 16
int parent[MAX_N];
int height[MAX_N];

void init(const int& n)
{
	for (int i = 0; i < n; ++i)
	{
		parent[i] = i;
		height[i] = 0;
	}
}

int find(const int& x)
{
	if (parent[x] == x)
	{
		return x;
	}
	else
	{
		return parent[x] = find(parent[x]);
	}
}

void unite(int x, int y)
{
	x = find(x);
	y = find(y);
	if (x == y)
	{
		return;
	}

	if (height[x] < height[y])
	{
		parent[x] = y;
	}
	else
	{
		parent[y] = x;
		if (height[x] == height[y])
		{
			++height[x];
		}
	}
}

bool same(const int& x, const int& y)
{
	return find(x) == find(y);
}
// End Of 并查集

struct edge
{
	int u, v, cost;
	edge(int u = 0, int v = 0, int cost = 0) : u(u), v(v), cost(cost) {}
	bool operator < (const edge & e2) const
	{
		return cost < e2.cost;
	}
};
edge es[MAX_E];
int V, E;
int kruskal()
{
	sort(es, es + E);	// 按照权值从小到大排序
	init(V);
	int res = 0;
	for (int i = 0; i < E; ++i)
	{
		edge e = es[i];
		if (!same(e.u, e.v))
		{
			unite(e.u, e.v);
			res += e.cost;
		}
	}

	return res;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
	// 测试数据就不手工填充了，好累(￣▽￣") 
	cin >> V >> E;
	for (int i = 0; i < E; ++i)
	{
		cin >> es[i].u >> es[i].v >> es[i].cost;
	}
	cout << kruskal() << endl;
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

知识共享署名-非商业性使用-相同方式共享：码农场 » 最小生成树算法初步