![]()

滑动拼图:也许你玩过15拼图:
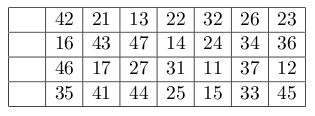
可你玩过28拼图吗?给定4*8的表格
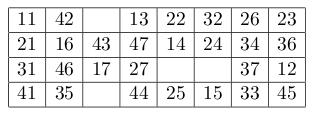
首先把11、21、31、41这四个数字提到第一列空白处:
然后按如下规则移动数字,定义某个空白处的左邻居+1为魔法数字,如果魔法数字存在,则可以将该魔法数字移动到该空白,比如42旁边的空白可以填充的魔法数字为43,而27则没有魔法数字,因为根本不存在28这个数。
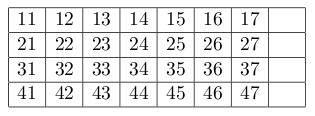
拼图的目标是达到如下效果:
求最小移动回数。
4.5开动脑筋智慧搜索
剪枝
题目本身没什么难度,模拟一个游戏规则,用BFS遍历所有状态。
复杂之处在于状态数非常之多,32个格子,28种数字,状态数一共有
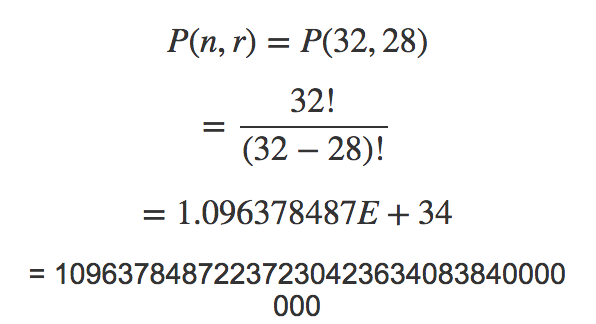
不可能用visited[]数组在内存里都表达出来,可以用HashSet来记录visited状态。由于C++98里面没有好用的HashSet,而陈腐的POJ又不支持C++11,所以干脆提交到了AOJ上去了 。
。
#include <iostream>
#include <cstring>
#include <climits>
#include <queue>
#include <unordered_set>
using namespace std;
class State
{
public:
/**
* 表格数字
*/
int table[4][8];
/**
* 移动回数
*/
int turn;
State(int card[4][7])
{
for (int i = 0; i < 4; i++)
table[i][0] = (10 * (i + 1) + 1);// 11 21 31 41
for (int i = 0; i < 4; i++)
{
memcpy(table[i] + 1, card[i], 7 * sizeof(int));
}
// 从这种布局开始游戏
for (int i = 0; i < 4; i++)
{
for (int j = 1; j < 8; j++)
{
if (table[i][j] == 11 || table[i][j] == 21 || table[i][j] == 31 || table[i][j] == 41)
table[i][j] = 0;
}
}
turn = 0;
}
State(const State &t)
{
memcpy(table, t.table, sizeof(table));
turn = t.turn;
}
/**
* 可以填充空白
* @param x
* @param y
* @return
*/
bool can_fill_gap(int x, int y)
{
if (table[x][y] != 0)
return false;
else if (table[x][y - 1] == 0 || (table[x][y - 1]) % 10 == 7) // x7 has no successor
return false;
else
return true;
}
/**
* 填充空白
* @param x
* @param y
*/
void fill_gap(int x, int y)
{
int s, sx, sy;
sx = sy = -1;
s = table[x][y - 1] + 1;
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 8; j++)
{
if (table[i][j] == s)
{
sx = i;
sy = j;
}
}
}
table[x][y] = table[sx][sy];
table[sx][sy] = 0;
turn++;
}
/**
* 是否是游戏结束状态,即每行都是升序,最后一列全为0
* @return
*/
bool done()
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 7; j++)
{
if (table[i][j] != (10 * (i + 1) + (j + 1)))
return false;
}
if (table[i][7] != 0)
return false;
}
return true;
}
bool operator==(const State &s) const
{
int i, j;
for (i = 0; i < 4; i++)
{
for (j = 1; j < 8; j++)
{
if (table[i][j] != s.table[i][j])
return false;
}
}
return true;
}
};
struct StateHash
{
size_t operator()(const State &s) const
{
size_t hash = 0;
for (int i = 0; i < 4; i++)
{
for (int j = 1; j < 8; j++)
{
hash += s.table[i][j];
hash <<= 1;
}
}
return hash;
}
};
int solve(int card[4][7])
{
queue<State> que;
unordered_set<State, StateHash> visited;
//准备BFS
bool end = false;
int ans = INT_MAX;
State init(card);
if (init.done())
return 0;
que.push(init);
visited.insert(init);
//BFS
while (!que.empty() && !end)
{
State s = que.front();
que.pop();
for (int i = 0; i < 4; i++)
{
for (int j = 1; j < 8; j++)
{
if (s.can_fill_gap(i, j))
{
State temp(s);
temp.fill_gap(i, j);
// 结束
if (temp.done())
{
end = true;
ans = temp.turn;
}// 未遍历
else if (visited.find(temp) == visited.end())
{
que.push(temp);
visited.insert(temp);
}
}
}
}
}
if (ans == INT_MAX)
ans = -1;
return ans;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int card[4][7];
for (int i = 0; i < 4; ++i)
{
for (int j = 0; j < 7; ++j)
{
scanf("%d", &card[i][j]);
}
}
printf("%d\n", solve(card));
}
return 0;
}

 码农场
码农场