POJ 1017 Packets 题解 《挑战程序设计竞赛(第2版)》练习题答案

2.2 一往直前！贪心法 其他

POJ 1017 Packets

有 1 * 1 到 6 * 6 的产品，最少用几个 6 * 6 的箱子装它们。

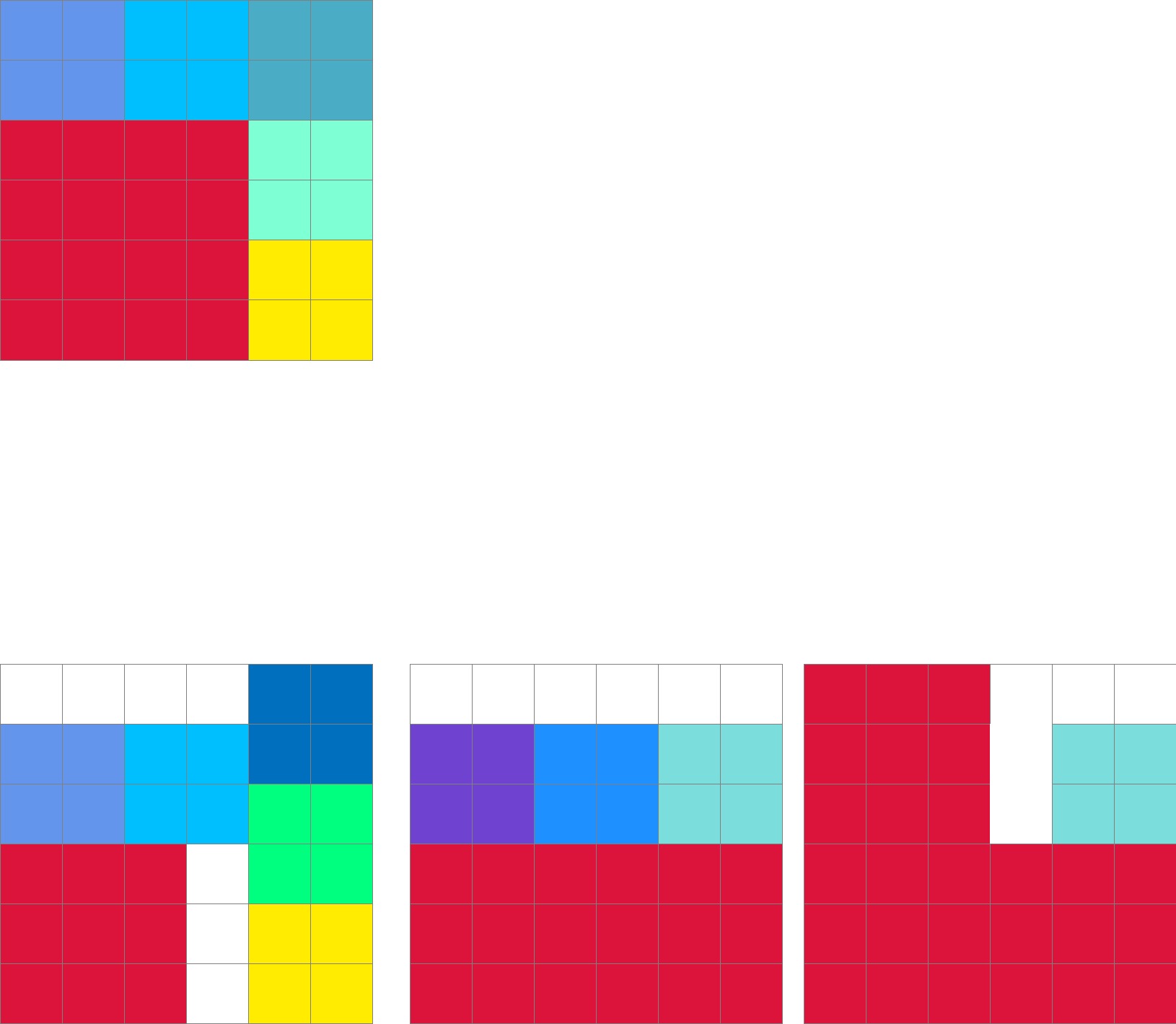
贪心策略是先装大的，再装小的，看我专门画的图就全明白了。生活常识，桶里先放碎石，再放沙，最后还可以装不少水。 6 * 6 和 5 * 5 以及 4 * 4 肯定独享一个箱子（不可能再放得下同规格的产品）。装了 4 * 4 和 3 * 3 的箱子还可以放 2 * 2 的产品，画个图就知道能放几个：

#include <iostream>
#include <cmath>
using namespace std;

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n, p1, p2, p3, p4, p5, p6, x , y;
	int space[4] = {0, 5, 3, 1}; // 一个箱子放入几个 3 * 3 后留下的缝隙可以放入几个 2 * 2
	while(true)
	{
		cin >> p1 >> p2 >> p3 >> p4 >> p5 >> p6;
		if(p1 == 0 && p2 == 0 && p3 == 0 && p4 == 0 && p5 == 0 && p6 == 0)
		{
			break;
		}
		// 第一次放“放不下第二个该型号”的型号，需要消耗n个箱子
		n = p4 + p5 + p6 + ceil(p3 / 4.0); // 对 3 * 3 的 package 来讲，四个刚好，否则向上取整
		// 计算 4 * 4 的型号和 3 * 3 的型号之间的缝隙可以放下多少个 2 * 2 的型号
		y = 5 * p4 + space[p3 % 4];
		// 2 * 2 的型号填入这些缝隙，如果填不下，再多消耗几个箱子
		if(p2 > y)
		{
			n += ceil((p2 - y) / 9.0); // 多出来的每9个刚好一个箱子
		}
		// 计算现在空了多少个 1 * 1 的位置
		x = 36 * n - 36 * p6 - 25 * p5 - 16 * p4 - 9 * p3 - 4 * p2;
		// 1 * 1 的型号填入这些缝隙，如果填不下，再多消耗几个箱子
		if(p1>x)
		{
			n += ceil((p1 - x) / 36.0);
		}
		cout << n << endl;
	}
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
    system("out.txt");
#endif
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1017 Packets 题解 《挑战程序设计竞赛(第2版)》练习题答案