POJ 3641 Pseudoprime numbers 题解 《挑战程序设计竞赛》

POJ 3641 Pseudoprime numbers

伪素数：满足①p不是素数②存在a > 1使得a^p = a (mod p)的p是伪素数，给出p和a，判断p是否是伪素数。

2.6 数学问题的解题窍门

快速幂运算

用反复平方法做快速幂运算判断条件②，条件①嘛，朴素的素性测试就行了。

有读者问我为什么特意写个函数LL mod_mult(LL a, LL b, LL m)来求(a * b) % m，因为这样不容易溢出。如果直接用运算符先*后%的话，哪怕是unsigned long long也可能溢出。

这个求余乘法的思想是，先将一个数用2进制表示：

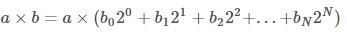
b_n表示b的二进制的第n个bit，当然，首个比特是从0开始算的。将a乘入括号中，得到：

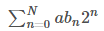
由于b_n要么是0要么是1，所以只需计算为1的部分就可以了，比如3*5：

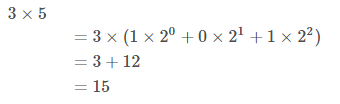
每加一次就求一次余，这样每次加上去的都是小于m的余数，这样就不怕溢出了。由于每个bit都需要计算一次，所以复杂度是O(log(N))。

#ifndef ONLINE_JUDGE
#pragma warning(disable : 4996)
#endif
#include <iostream>
using namespace std;

typedef long long LL;

// return (a * b) % m
LL mod_mult(LL a, LL b, LL m)
{
	LL res = 0;
	LL exp = a % m;
	while (b)
	{
		if (b & 1)
		{
			res += exp;
			if (res > m) res -= m;
		}
		exp <<= 1;
		if (exp > m) exp -= m;
		b >>= 1;
	}
	return res;
}

// return (a ^ b) % m
LL mod_exp(LL a, LL b, LL m) 
{
	LL res = 1;
	LL exp = a % m;
	while (b)
	{
		if (b & 1) res = mod_mult(res, exp, m);
		exp = mod_mult(exp, exp, m);
		b >>= 1;
	}
	return res;
}

//************************************
// Method:    is_prime
// FullName:  is_prime
// Access:    public 
// Returns:   bool
// Qualifier: 素性测试
// Parameter: const int & n
//************************************
bool is_prime(const int& n)
{
	for (int i = 2; i * i <= n; ++i)
	{
		if (n % i == 0)
		{
			return false;
		}
	}

	return n != 1;	// 1是例外
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int p, a;
	while (cin >> p >> a && p && a)
	{
		if (!is_prime(p) && (mod_exp(a, p, p) == a))
		{
			cout << "yes" << endl;
		}
		else
		{
			cout << "no" << endl;
		}
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3641 Pseudoprime numbers 题解 《挑战程序设计竞赛》