RSA加密算法的地位无需赘述,其代码实现也多如牛毛,但徒手计算的能力仍然是有趣并有用的,这是内在修养。本文关注的是面向手工的计算方法,虽然拓展欧几里得算法不过三五行代码,但给你一支笔和一张纸,如何迅速地算出可靠结果呢?

援引《图解密码技术》中的例子,原著并未提供手算方法,在此做一个补充。
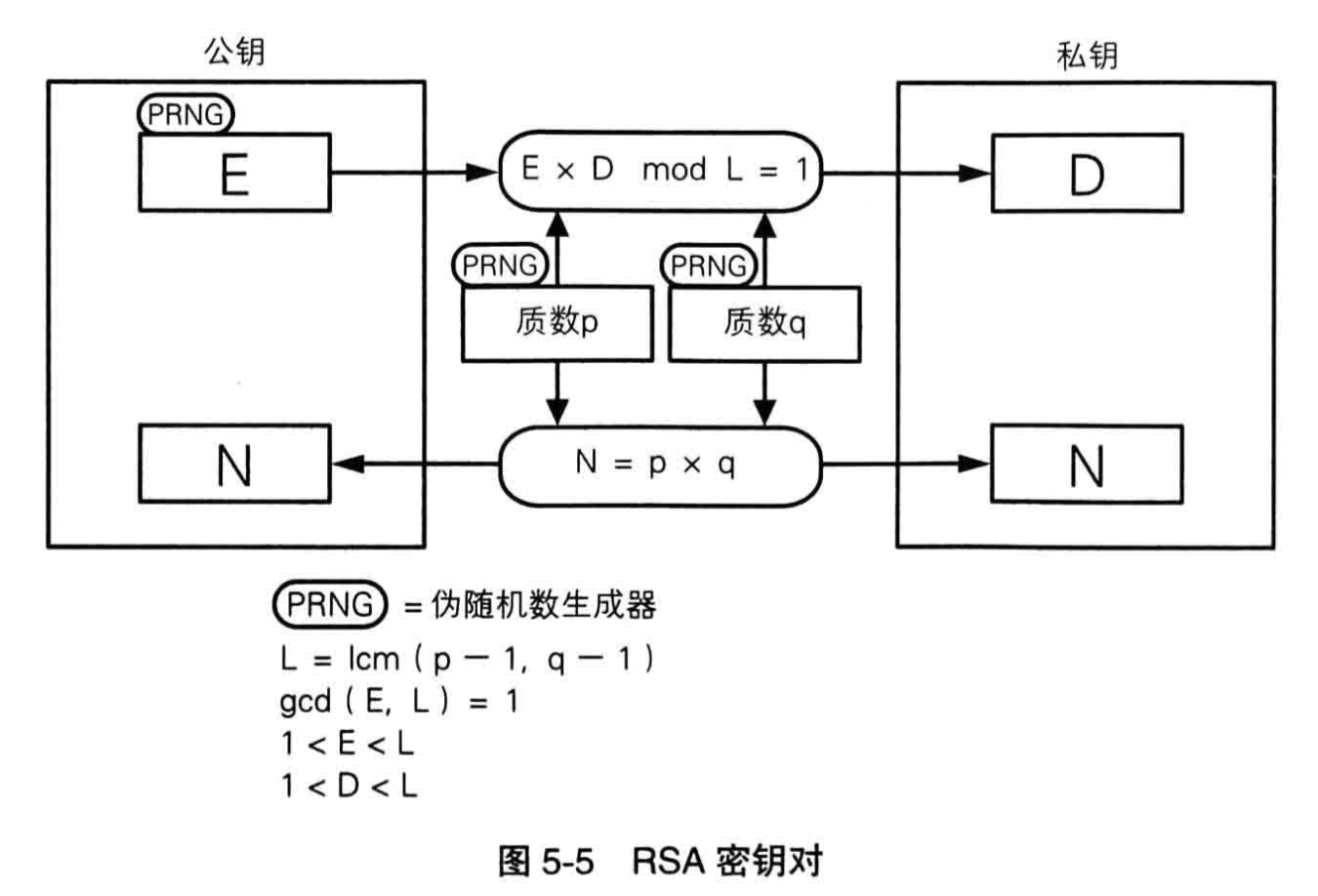
公钥(E,N)
选定如下两个质数:
p=17
q=19
那么,N=p*q=323,N就是公钥的一部分,来看看另一部分E怎么找到。
定义中间结果L=lcm(p-1,q-1),也就是这两个数的最小公倍数,那么L=lcm(16,18)=144。
事实上,中间结果还有另外一种定义,即phi(N),也即欧拉函数,既然N是两个质数的积,那么就有phi(N)=(p-1)(q-1)=288。
E和L必须互质,且E<L。为了方便计算,就选最小的那个:E=5;于是公钥就选定了——(5,323)
私钥D
解方程ED mod L = 1,其中E=5、L=144。用拓展欧几里得算法,但不是运行在PC里的,而是运行在我们大脑里,通过纸笔进行输出。原著草草给了最终答案,显然这并不够。
对于这个方程,我们写成更具体的约束形式,对最终的解D,必然满足:
Ex+Ly=1;其中,x就是D,而y是与D相应的一个数,在RSA算法中并不关心。
列出表头
| u' | u | x' | x | y' | y | q |
其中,u表示余数,在初始状态下,u'和u分别表示L和E,这类似于代码中的a和b,前者必须大于后者,这也是为什么上面规定L>E的原因,上标的撇表示上一轮运算结果;q表示u'除以u的商。
填入初始状态
既然明白了表头的含义,就可以填入初始值了:
| u' | u | x' | x | y' | y | q |
| 144 | 5 | 0 | 1 | 1 | 0 |
递推下一行
q=u'/u=144/5=28,余4。所以u'=u=5,而u=4。x = x' – xq = 0 – 1 * 28 = -28,y = y' – yq = 1 – 0 * 28 = 1。x' = x = 1, y' = y = 0。更新第二行:
| u' | u | x' | x | y' | y | q |
| 144 | 5 | 0 | 1 | 1 | 0 | 28 |
| 5 | 4 | 1 | -28 | 0 | 1 |
递推所有行
这个运算并不复杂,按照上述步骤一直往下算,直到u=0,也即u'能被u整除:
| u' | u | x' | x | y' | y | q |
| 144 | 5 | 0 | 1 | 1 | 0 | 28 |
| 5 | 4 | 1 | -28 | 0 | 1 | 1 |
| 4 | 1 | -28 | 29 | 1 | -1 | 4 |
| 1 | 0 |
事实上在上一步的基础上,我们才算了一行就发现4能被1整除,于是终止了运算。我们可以代入Ex+Ly=1验算一下:
5 * 29 + 144 * (-1) = 145 – 144 = 1 ,没有问题。
那么x = 29 mod 144 = 29 ,就是最终的解。
于是我们顺利地求出了私钥D = 29 ,这跟原著是一致的,但我们完全靠自己和纸笔求出来了。
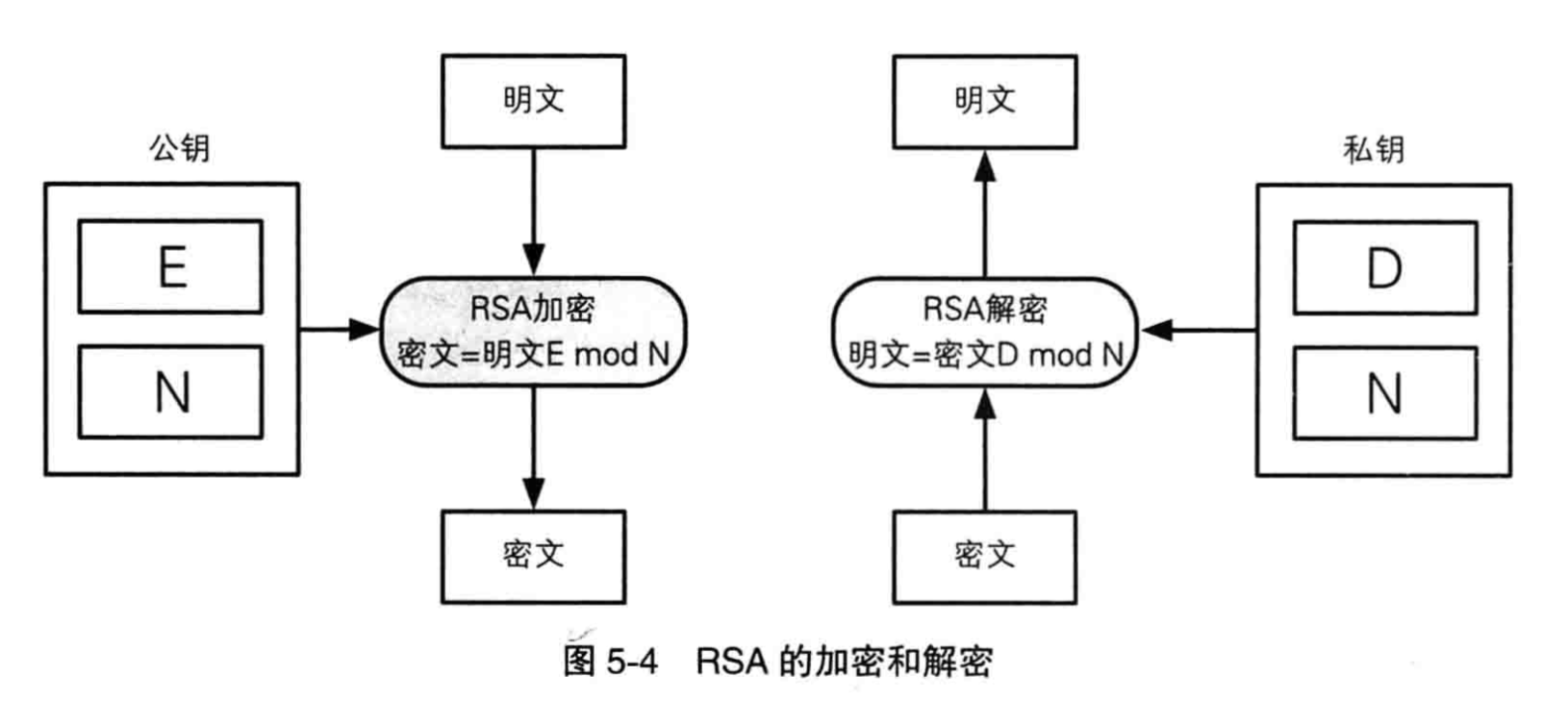
至于加密解密,反而更加简单,请参考任何一部密码学书籍。
 码农场
码农场
表头写成L,E,D’ , D , Y’, Y ,C 更容易做考试题哈。