通用维特比算法的Java实现

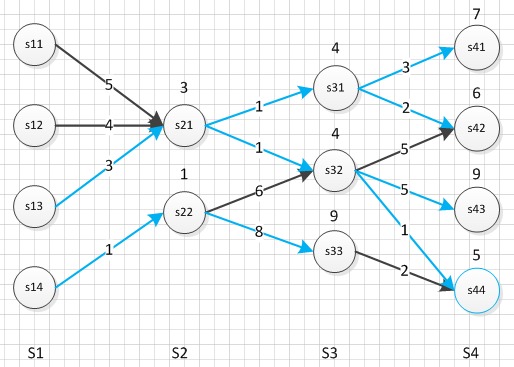
用Java实现的求解HMM的维特比算法，开源在Git上:https://github.com/hankcs/Viterbi。代码本身没什么新意，看到Git上没有好用的Viterbi的Java实现，所以补个缺。特点是简单好懂，一个方法搞定。调用简单，往compute方法里填充HMM的五元组就能得到最佳标注序列。

附赠一个对经典天气预测问题的求解，问题的描述和思路详见前文：

package com.hankcs.algorithm;

import static com.hankcs.algorithm.Main.Weather.*;
import static com.hankcs.algorithm.Main.Activity.*;

public class Main
{
    static enum Weather
    {
        Rainy,
        Sunny,
    }
    static enum Activity
    {
        walk,
        shop,
        clean,
    }
    static int[] states = new int[]{Rainy.ordinal(), Sunny.ordinal()};
    static int[] observations = new int[]{walk.ordinal(), shop.ordinal(), clean.ordinal()};
    static double[] start_probability = new double[]{0.6, 0.4};
    static double[][] transititon_probability = new double[][]{
            {0.7, 0.3},
            {0.4, 0.6},
    };
    static double[][] emission_probability = new double[][]{
            {0.1, 0.4, 0.5},
            {0.6, 0.3, 0.1},
    };

    public static void main(String[] args)
    {
        int[] result = Viterbi.compute(observations, states, start_probability, transititon_probability, emission_probability);
        for (int r : result)
        {
            System.out.print(Weather.values()[r] + " ");
        }
        System.out.println();
    }
}

输出：

Sunny Rainy Rainy

顺便贴一个源码：

package com.hankcs.algorithm;

/**
 * 维特比算法
 * @author hankcs
 */
public class Viterbi
{
    /**
     * 求解HMM模型
     * @param obs 观测序列
     * @param states 隐状态
     * @param start_p 初始概率（隐状态）
     * @param trans_p 转移概率（隐状态）
     * @param emit_p 发射概率 （隐状态表现为显状态的概率）
     * @return 最可能的序列
     */
    public static int[] compute(int[] obs, int[] states, double[] start_p, double[][] trans_p, double[][] emit_p)
    {
        double[][] V = new double[obs.length][states.length];
        int[][] path = new int[states.length][obs.length];

        for (int y : states)
        {
            V[0][y] = start_p[y] * emit_p[y][obs[0]];
            path[y][0] = y;
        }

        for (int t = 1; t < obs.length; ++t)
        {
            int[][] newpath = new int[states.length][obs.length];

            for (int y : states)
            {
                double prob = -1;
                int state;
                for (int y0 : states)
                {
                    double nprob = V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]];
                    if (nprob > prob)
                    {
                        prob = nprob;
                        state = y0;
                        // 记录最大概率
                        V[t][y] = prob;
                        // 记录路径
                        System.arraycopy(path[state], 0, newpath[y], 0, t);
                        newpath[y][t] = y;
                    }
                }
            }

            path = newpath;
        }

        double prob = -1;
        int state = 0;
        for (int y : states)
        {
            if (V[obs.length - 1][y] > prob)
            {
                prob = V[obs.length - 1][y];
                state = y;
            }
        }

        return path[state];
    }
}

对，你没看错，就这么点代码。

有些人主张代码有问题，我并非反对质疑精神，只建议这些人参考 http://www.hankcs.com/ml/hidden-markov-model.html#h3-20 这段动画，认认真真把算法单步一遍，再提出具体哪个数据有问题。治学需谨慎，用试验数据说话。

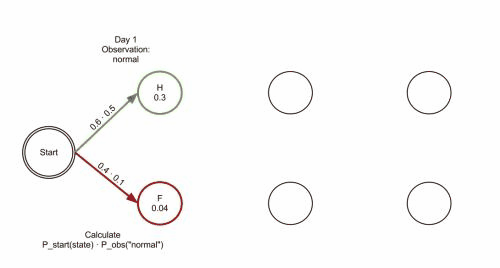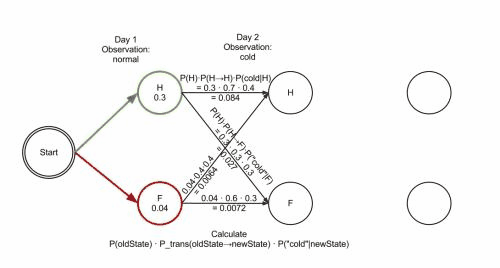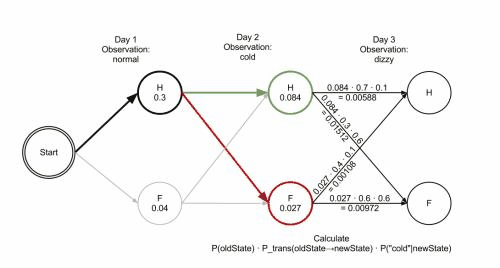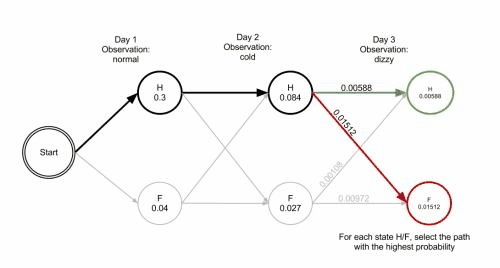
最终路径的概率prob=0.01512、每一步的两种可能的概率、都与动画完全一致，与Python实现也完全一致。

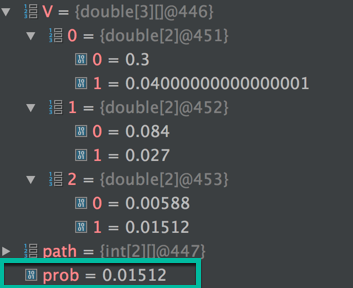
有问题请上GitHub提issue，或者直接用你认为“正确”的代码覆盖我的代码，然后pull request给我。不要在评论里面人云亦云。

 知识共享署名-非商业性使用-相同方式共享：码农场 » 通用维特比算法的Java实现