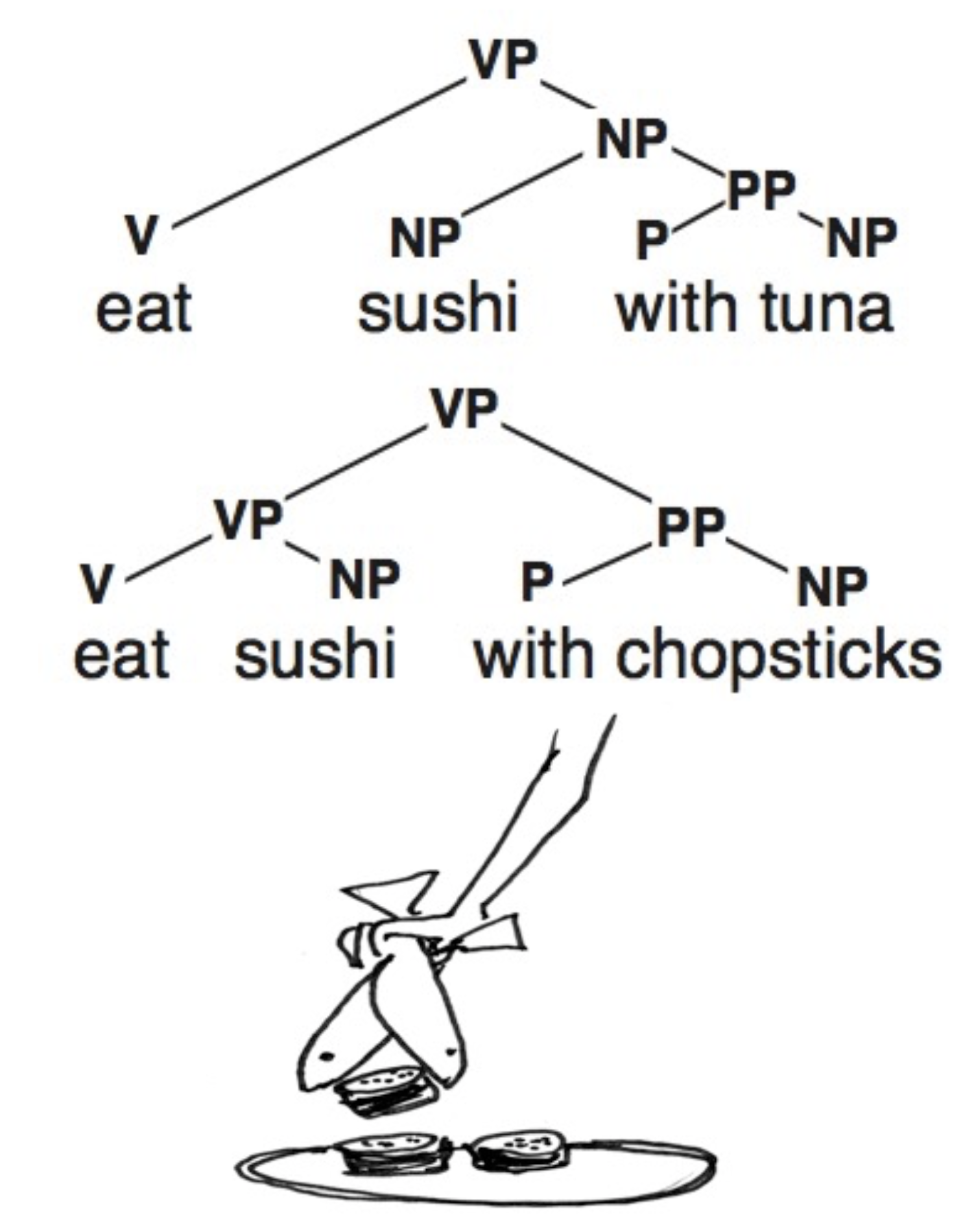
Micheal Collins在Coursera上的自然语言处理公开课,第二次任务。自然语言中的歧义令人忍俊不禁,只要你或者你的模型脑洞足够大。

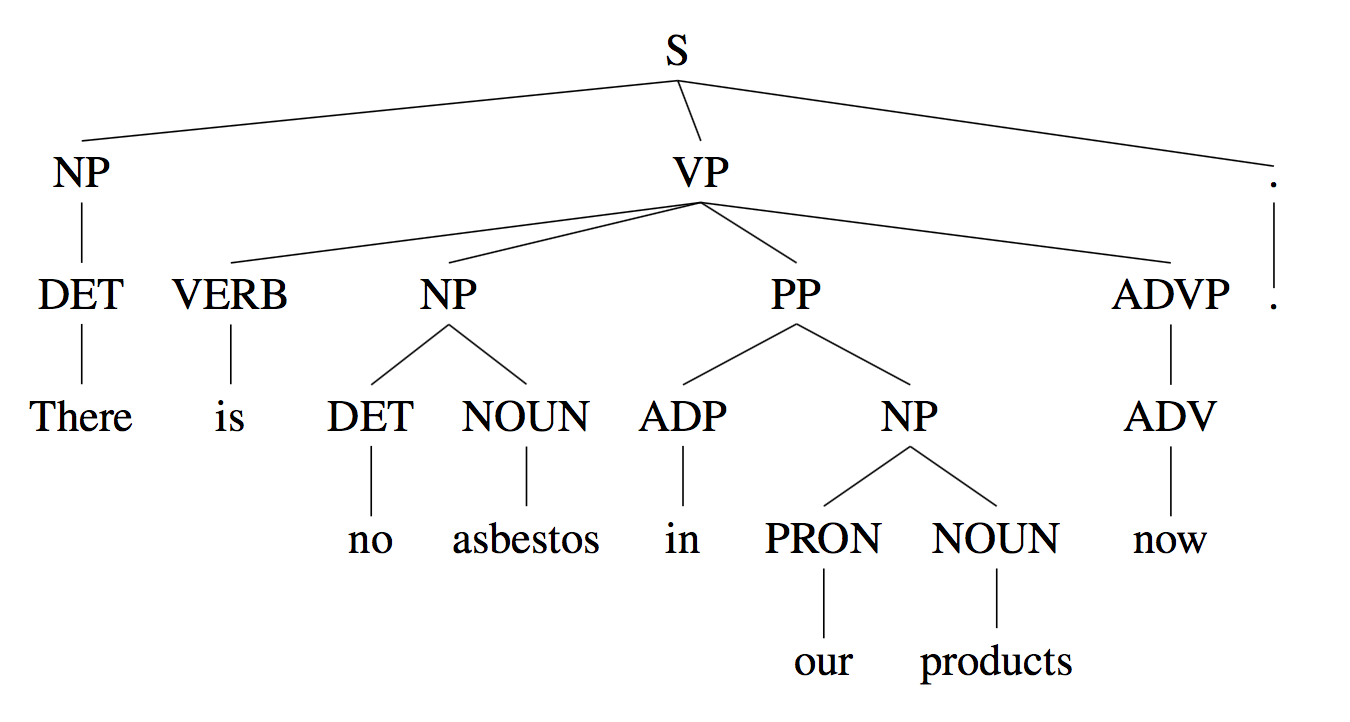
语料库来自WSJ,但并不是乔姆斯基范式:
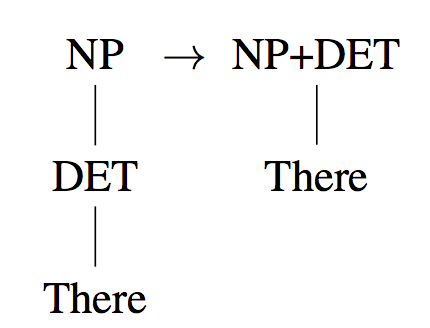
因为乔姆斯基范式中一元rule必须是叶子节点,修正方案是折叠过长的路径:
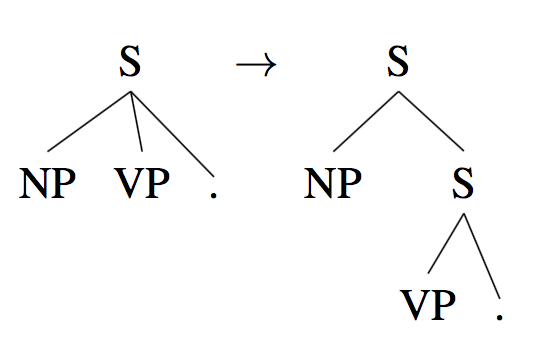
也不可能出现多于2元的rule,修正方案是将多余的分支统一移入右子树:
assignment中附带的语料已经经过了上述修正处理,无需担心。语料格式被预处理为多级嵌套的json数组:
二元——

一元——

整棵树——
["S", ["NP", ["DET", "There"]], ["S", ["VP", ["VERB", "is"], ["VP", ["NP", ["DET", "no"], ["NOUN", "asbestos"]], ["VP", ["PP", ["ADP", "in"], ["NP", ["PRON", "our"], ["NOUN", "products"]]], ["ADVP", ["ADV", "now"]]]]], [".", "."]]]
assignment提供了一个pretty_print_tree.py脚本来打印短语结构树,但不支持不规范的结构树,会抛出如下异常:
Traceback (most recent call last):
File "pretty_print_tree.py", line 50, in <module>
main(sys.argv[1])
File "pretty_print_tree.py", line 38, in main
pretty_print_tree(json.loads(l))
File "pretty_print_tree.py", line 34, in pretty_print_tree
print pprint.pformat(tree)
File "python2.7/pprint.py", line 63, in pformat
return PrettyPrinter(indent=indent, width=width, depth=depth).pformat(object)
File "python2.7/pprint.py", line 122, in pformat
self._format(object, sio, 0, 0, {}, 0)
File "python2.7/pprint.py", line 140, in _format
rep = self._repr(object, context, level - 1)
File "python2.7/pprint.py", line 226, in _repr
self._depth, level)
File "python2.7/pprint.py", line 238, in format
return _safe_repr(object, context, maxlevels, level)
File "python2.7/pprint.py", line 314, in _safe_repr
orepr, oreadable, orecur = _safe_repr(o, context, maxlevels, level)
File "python2.7/pprint.py", line 314, in _safe_repr
orepr, oreadable, orecur = _safe_repr(o, context, maxlevels, level)
File "python2.7/pprint.py", line 323, in _safe_repr
rep = repr(object)
TypeError: __repr__ returned non-string (type list)
需要作如下修改:
class Node: """ Dummy class for python's pretty printer. """ def __init__(self, name): if isinstance(name, list): name = ','.join(name) self.name = name def __repr__(self): return self.name
然后就可以打印出来了:
[S, [NP, DET,There], [S, [VP, [VERB, is], [VP, [NP, [DET, no], [NOUN, asbestos]], [VP, [PP, [ADP, in], [NP, [PRON, our], [NOUN, products]]], [ADVP, ADV,now]]]], [., .]]]
问题1
如同标注模型一样,我们需要统计训练语料中的词语概率,于是就会遇到低频词问题。请将词频小于5的低频词统一替换为一个特殊符号。
算是热身运动,有助于理解语料格式,通过assignment中附带的Counts对象统计规则和non-terminate的频次:
"""
Count rule frequencies in a binarized CFG.
"""
class Counts(object):
def __init__(self):
self.unary = {}
self.binary = {}
self.nonterm = {}
def show(self):
for symbol, count in self.nonterm.iteritems():
print count, "NONTERMINAL", symbol
for (sym, word), count in self.unary.iteritems():
print count, "UNARYRULE", sym, word
for (sym, y1, y2), count in self.binary.iteritems():
print count, "BINARYRULE", sym, y1, y2
def count(self, tree):
"""
Count the frequencies of non-terminals and rules in the tree.
"""
if not isinstance(tree, list): return
# Count the non-terminal symbol.
symbol = tree[0]
self.nonterm.setdefault(symbol, 0)
self.nonterm[symbol] += 1
if len(tree) == 3:
# It is a binary rule.
y1, y2 = (tree[1][0], tree[2][0])
key = (symbol, y1, y2)
self.binary.setdefault(key, 0)
self.binary[(symbol, y1, y2)] += 1
# Recursively count the children.
self.count(tree[1])
self.count(tree[2])
elif len(tree) == 2:
# It is a unary rule.
y1 = tree[1]
key = (symbol, y1)
self.unary.setdefault(key, 0)
self.unary[key] += 1
这个递归函数执行先序遍历,通过root的长度判断是一元还是二元,并对二元执行递归。
可见nonterm中存放所有symbol,unary存放一元rule,binary存放二元rule。要统计词频的话,遍历unary这个dict即可:
def count_word(self): ''' count emitted words and find rare words ''' # count emitted word for (sym, word), count in self.unary.iteritems(): self.word[word] += count # find rare word for word, count in self.word.iteritems(): if count < RARE_WORD_THRESHOLD: self.rare_words.append(word)
有了词频,替换低频词就好说了,依然是一个递归调用:
def process_rare_words(input_file, output_file, rare_words, processer):
"""
替换低频词,并输出到文件
:param input_file:
:param output_file:
:param rare_words:
:param processer:
"""
for line in input_file:
tree = json.loads(line)
replace(tree, rare_words, processer)
output = json.dumps(tree)
output_file.write(output)
output_file.write('\n')
def replace(tree, rare_words, processer):
"""
替换一棵树中的低频词
:param tree:
:param rare_words:
:param processer:
:return:
"""
if isinstance(tree, basestring):
return
if len(tree) == 3:
# Recursively count the children.
replace(tree[1], rare_words, processer)
replace(tree[2], rare_words, processer)
elif len(tree) == 2:
if tree[1] in rare_words:
tree[1] = processer(tree[1])
最终输出parser_train.counts.out文件:
1 NONTERMINAL NP+ADVP 254 NONTERMINAL VP+VERB 65 NONTERMINAL SBAR 81 NONTERMINAL ADJP 30 NONTERMINAL WHADVP
问题2
请通过最大似然估计PCFG的参数:
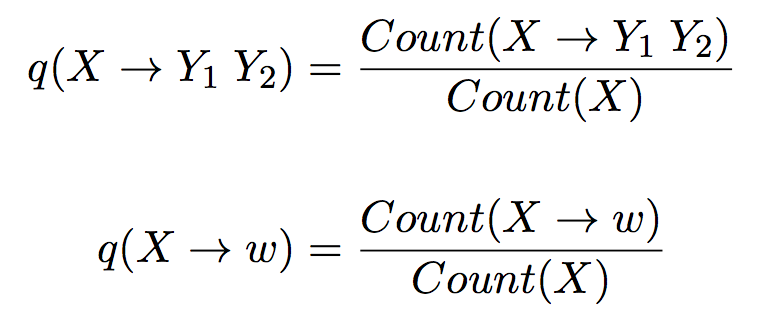
再简单不过了:
def cal_rule_params(self): """ 统计uni和bin rule的频率 """ # q(X->Y1Y2) = Count(X->Y1Y2) / Count(X) for (x, y1, y2), count in self.binary.iteritems(): key = (x, y1, y2) self.q_x_y1y2[key] = float(count) / float(self.nonterm[x]) # q(X->w) = Count(X->w) / Count(X) for (x, w), count in self.unary.iteritems(): key = (x, w) self.q_x_w[key] = float(count) / float(self.nonterm[x])
有了模型参数,请实现CKY算法以计算![]() 。
。
先引入记号:
n为句子中的单词数
w_i表示第i个单词
N表示语法中的non-terminal个数
S表示语法中的start symbol
定义动态规划表格:
![]() 表示从单词i到j的这部分句子构成以X作为根节点的最大概率。那么我们的目标就是要计算
表示从单词i到j的这部分句子构成以X作为根节点的最大概率。那么我们的目标就是要计算![]() 。
。
对于pi的定义,进一步说明如下:
当i=j时,有![]()
否则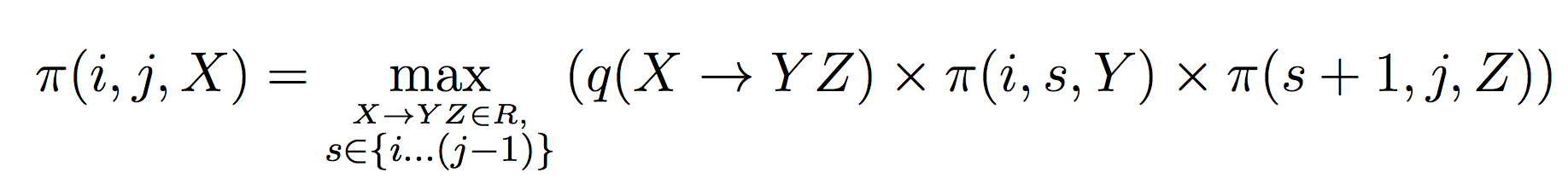
完整的CKY算法如下

第一层循环选定pi的长度,从1开始,第二层循环选取pi的起点i,于是终点j就确定下来了。
第三层循环遍历X的所有可能情况,也就是选定X。然后这层循环里面干了最重要的事情,继续遍历X->YZ的所有情况,选定X->YZ,遍历i到j之间的每个位置s,切一刀,算出概率取最大值赋给pi;同时记录得到最大值时的X->YZ和s。
Python实现如下:
def CKY(self, sentence):
pi = defaultdict()
bp = defaultdict()
N = self.nonterm.keys()
words = sentence.strip().split(' ')
n = len(words)
# process rare word,测试文件中的未登录词按照相同的规则预处理
for i in xrange(0, n):
if words[i] not in self.word.keys():
words[i] = self.rare_words_rule(words[i])
log('Sentence to process: {sent}'.format(sent=' '.join(words)))
log('n = {n}, len(N) = {ln}'.format(n=n, ln=len(N)))
# reduce X, Y and Z searching space,剪枝策略,过滤掉那些不合法的rule
SET_X = defaultdict()
for (X, Y, Z) in self.binary.keys():
if X in SET_X:
SET_X[X].append((Y, Z))
else:
SET_X[X] = []
# init, unary rule
for i in xrange(1, n + 1):
w = words[i - 1]
for X in N:
if (X, w) in self.unary.keys():
pi[(i, i, X)] = Decimal(self.q_x_w[(X, w)])
else:
pi[(i, i, X)] = Decimal(0.0)
# dp
for l in xrange(1, n):
for i in xrange(1, n - l + 1):
j = i + l
for X, YZPairs in SET_X.iteritems():
cur_pi, max_pi = 0.0, -1.0
for (Y, Z) in YZPairs:
for s in xrange(i, j):
# 由于我们用SET_X做了剪枝,所以需要检查是否属于被过滤掉的非法rule
if (i, s, Y) not in pi or (s + 1, j, Z) not in pi:
continue
cur_pi = Decimal(self.q_x_y1y2[(X, Y, Z)]) \
* pi[(i, s, Y)] \
* pi[(s + 1, j, Z)]
if cur_pi > max_pi:
max_pi = cur_pi
max_Y, max_Z, max_s = Y, Z, s
pi[(i, j, X)] = max_pi
bp[(i, j, X)] = (max_Y, max_Z, max_s)
if (1, n, ROOT) not in bp:
max_pi = 0.0
max_X = ''
for X, YZPairs in SET_X.iteritems():
if (1, n, X) in pi and pi[(1, n, X)] > max_pi:
max_pi = pi[(1, n, X)]
max_X = X
else:
max_X = ROOT
result = self.traceback(pi, bp, sentence, 1, n, max_X)
return result
如果不使用SET_X剪枝策略的话,代码外观可能跟伪码更加匹配,或者说更有简洁的美感,但很多unary的X会降低效率。
bp是一个回溯的数据结构,通过回溯还原一棵由嵌套数组组成的短语句法树:
def traceback(self, pi, bp, sentence, i, j, X):
words = sentence.strip().split(' ')
tree = []
tree.append(X)
if i == j:
tree.append(words[i - 1])
else:
Y1, Y2, s = bp[(i, j, X)]
# print Y1, Y2, s
tree.append(self.traceback(pi, bp, sentence, i, s, Y1))
tree.append(self.traceback(pi, bp, sentence, s + 1, j, Y2))
return tree
通过如下脚本运行评估脚本:
#!/usr/bin/env bash python eval_parser.py parse_dev.key p2.result
得到
Type Total Precision Recall F1-Score =============================================================== ADJP 13 0.231 0.231 0.231 ADVP 20 0.800 0.200 0.320 NP 1081 0.714 0.759 0.736 PP 326 0.775 0.794 0.785 PRT 6 0.500 0.333 0.400 QP 2 0.000 0.000 0.000 S 45 0.632 0.267 0.375 SBAR 15 0.500 0.333 0.400 SBARQ 488 0.974 0.998 0.986 SQ 488 0.846 0.867 0.856 VP 305 0.701 0.407 0.515 WHADJP 43 0.375 0.070 0.118 WHADVP 125 0.774 0.960 0.857 WHNP 372 0.885 0.825 0.854 WHPP 10 0.000 0.000 0.000 total 3339 0.798 0.770 0.783
如此简单朴素的CKY算法也能获得78%的F1值,挺不错了。
问题3
考虑如下句法树:
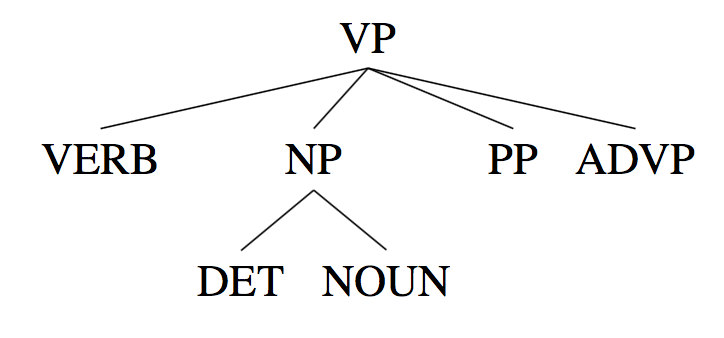
PCFG假设NP → DT NOUN 与父节点VP没有任何关系:
p(VP → VERB NP PP ADVP | VP) × p(NP → DET NOUN | NP)
这个假设实在太强烈了,父节点non-terminal对子节点rule的推断也应当有帮助:
p(VP → VERB NP PP ADVP | VP) × p(NP → DET NOUN | NP, parent=VP)
这种思想类似于trigram语言模型,要实现它只需改动一点点,即将子non-terminal加一个上标,上标为父节点:
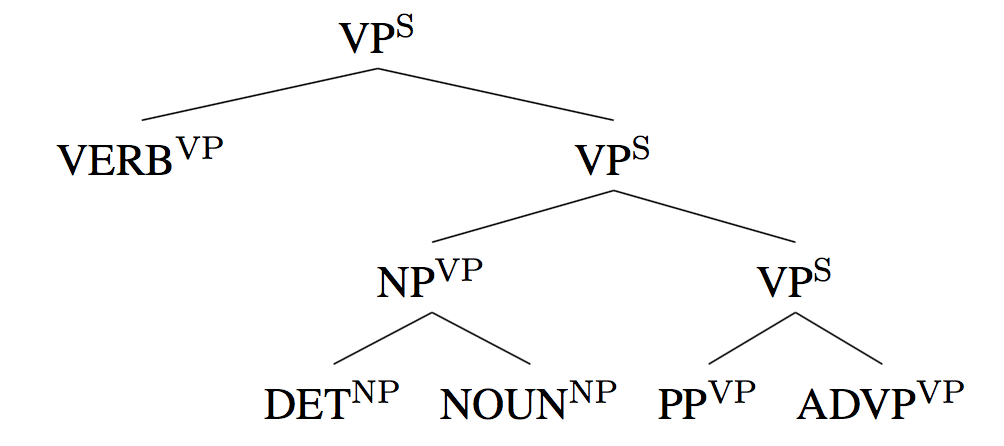
虽然这增加了non-terminal的数量,使得每个rule更加稀疏,但实践证明这种做法是有效的。请实现它,其中句法树的改进版本已经提供,直接使用即可。
没什么难度,命令行参数改改跑跑,得到的结果果然好一些:
Type Total Precision Recall F1-Score =============================================================== ADJP 13 0.375 0.231 0.286 ADVP 20 0.714 0.250 0.370 NP 1081 0.741 0.807 0.773 PP 326 0.780 0.816 0.798 PRT 6 0.250 0.167 0.200 QP 2 0.000 0.000 0.000 S 45 0.542 0.289 0.377 SBAR 15 0.250 0.200 0.222 SBARQ 488 0.976 0.998 0.987 SQ 488 0.948 0.969 0.958 VP 305 0.612 0.413 0.493 WHADJP 43 0.931 0.628 0.750 WHADVP 125 0.873 0.992 0.929 WHNP 372 0.957 0.901 0.928 WHPP 10 0.000 0.000 0.000 total 3339 0.830 0.819 0.824
Reference
https://github.com/hankcs/Coursera_NLP_MC
 码农场
码农场