Deep Biaffine Attention for Neural Dependency Parsing

这是斯坦福专攻Dependency Parsing的博士生Dozat在ICLR 2017上的论文，拿到了graph-based方法中的最高分，改进版还拿到了CoNLL 2017 Shared Task的第一。

基于图的依存句法分析需要解决两个问题：1、哪两个节点连依存弧；2、弧的标签是什么。NN方法使用分类器来解决这两个问题，记feature detector得到的特征向量为$\mathbf{r}_i$。

arc得分

这是一个不定类别的多分类问题。若句子中有$n$个单词，包含虚根ROOT在内一共$d=n+1$个token。对每个token来讲，都需要得到一个分数向量$\mathbf{s}_i \in \mathbb{R}^{d\times1}$。所有token构成$\mathbb{R}^{d \times d}$的分数矩阵，最后根据arc-factored原理找MST。

而一般MLP是个固定类别的分类器：

$$\begin{align}
 \label{tra-class}\mathbf{s}_i &= W\mathbf{r}_i + \mathbf{b} \end{align}$$

无法处理不定类别分类，所以作者提出先将$\mathbf{r}_i$重新encode为$\mathbb{R}^{k \times 1}$，也就是过一遍MLP：

$$\begin{align}
 \label{arc-dep}\mathbf{h}_i^{(arc-dep)} &= \text{MLP}^{(arc-dep)}(\mathbf{r}_i)\\
 \mathbf{h}_j^{(arc-head)} &= \text{MLP}^{(arc-head)}(\mathbf{r}_j)
\end{align}$$

这里两个MLP分别是dep专用和head专用。$k$的量级通常更小，压缩encode的另一个好处是去除多余的信息。因为原始$\mathbf{r}_i$中含有预测依存弧标签的信息，这对预测head来讲是赘余的。

特征降维了之后，权值矩阵和偏置也必须做出调整。作者提出用两个矩阵连乘（两次仿射变换biaffine）输入向量:

$$\label{arc-score}\mathbf{s}^{(arc)}_i = H^{(arc-head)}U^{(1)}\mathbf{h}^{(arc-dep)}_i+ H^{(arc-head)}\mathbf{u}^{(2)}$$

其中，矩阵$H$是$d$个token的特征经过MLP二次encode出来的特征向量$\mathbf{h}$的stack形式，上式维度变化是：

$$(d\times k) (k\times k)(k\times 1)+(d\times k)(k\times 1)=(d\times 1)$$

结果是拿到了$d$个token的分数$\mathbb{R}^{d\times1}$，同时分类器又不需要维护多个不同大小的权值矩阵（只需一个$\mathbb{R}^{k\times k}$的矩阵和两个MLP），漂亮地实现了可变类别分类。

如果把偏置放到$U^{(1)}$里面去，同时进行d个token的运算，则上式的维度变化是：

$$(d\times (k+1)) ((k+1)\times k)(k\times d)=(d\times d)$$

作者称这3个式子为deep bilinear attention mechanism，因为不同于直接用RNN输出的feature （shallow），这里通过MLP二次encode了一下。叫attention的原因是，输入是所有时刻的RNN feature，输出是一个在各个时刻上归一化的向量。

整个网络的架构如作者的Figure所示：

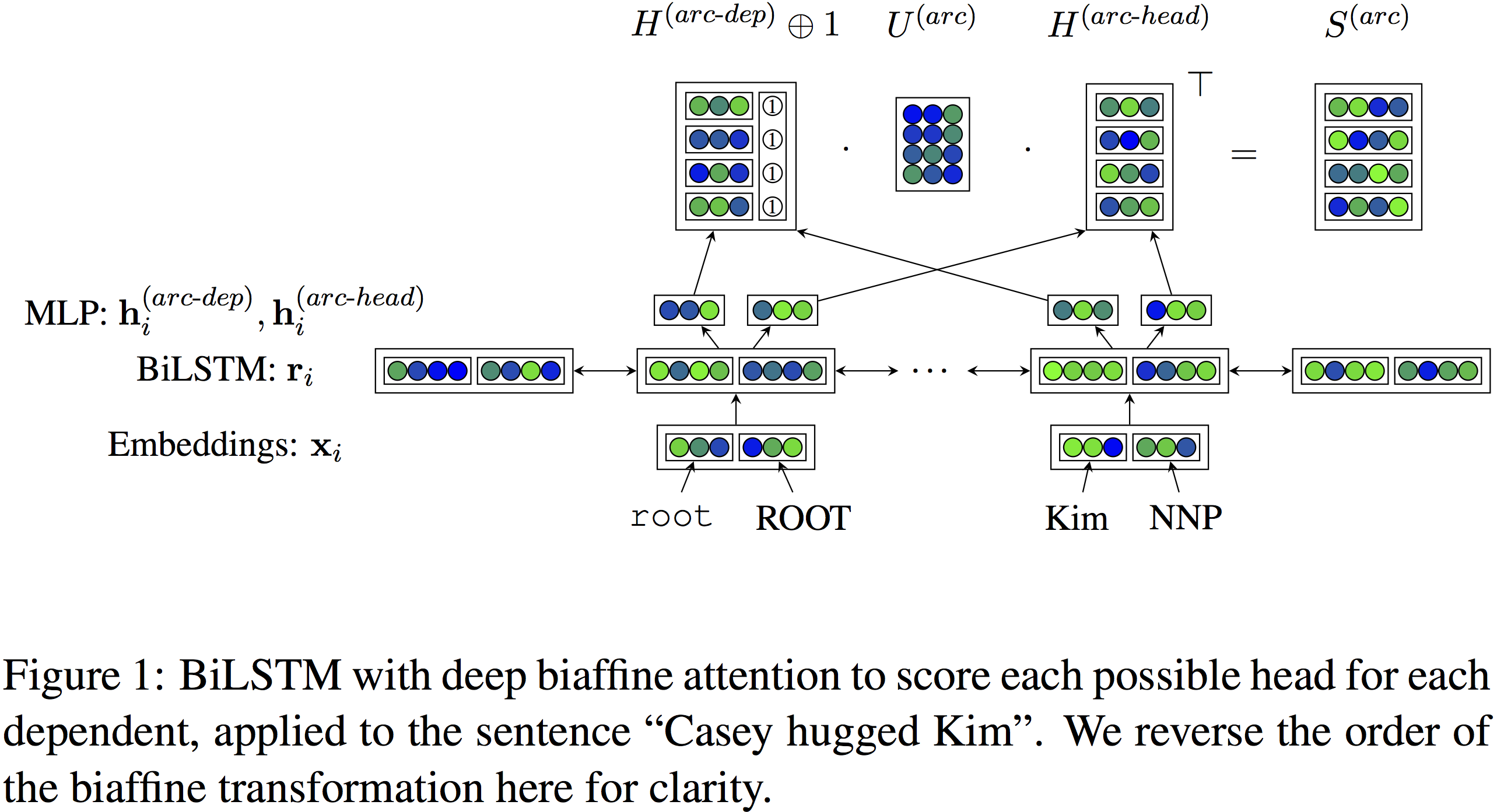
从下往上看，输入是word以及pos的embedding拼接，BiLSTM提取到特征$\mathbf{r}_i$，经过两个不同的MLP分别得到 $\mathbf{h}_i^{(arc-dep)}$ 和 $\mathbf{h}_j^{(arc-head)}$ ，$d$个这样的$\mathbf{h}$ stack起来分别构成了$H^{(arc-dep)}$和$H^{(arc-head)}$。其中由于bias的原因，$H^{(arc-dep)}$额外拼接了一个单位向量。经过一个中间矩阵$U^{(arc)}$仿射变换后，每个token以dep的身份与以head的身份的每个token进行一次点积，得到arc成立的分数矩阵$S^{(arc)}$。

arc标签

这是个固定类别的分类问题，作者认为必须同时考虑依存关系的先验概率，已知词语作为head或dep接受某种依存关系的后验概率。也就是下式：

$$\begin{align}
 \label{biaff-class}\mathbf{s}_i^{(label)} &= \mathbf{r}_{y_i}^\top \mathbf{U}^{(1)}\mathbf{r}_i + (\mathbf{r}_{y_i} \oplus \mathbf{r}_i)^\top U^{(2)} + \mathbf{b}\end{align}$$

第一项是同时已知$i$作为dep、$y_i$作为head情况下的后验概率，第二项是已知$i$或$y_i$是arc两端的后验概率，第三项偏置是什么都不知道时label的先验概率。

为什么第二项的$\oplus$可以这么解读呢？拼接的话向量有先后顺序的呀？难道不应该用没有顺序的求和吗？

来看看两个向量（书写简便，就用仅含有一个元素的“向量”做例子）$x_1$和$x_2$的拼接乘上一个矩阵会发生什么：

$$\left( {\begin{array}{*{20}{c}}
 {\begin{array}{*{20}{c}}
 a  \\
 b  \\
 c
\end{array}}&{\begin{array}{*{20}{c}}
 d  \\
 e  \\
 f
\end{array}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
 {{x_1}}  \\
 {{x_2}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
 {a{x_1} + d{x_2}}  \\
 {b{x_1} + e{x_2}}  \\
 {c{x_1} + f{x_2}}
\end{array}} \right)$$

结果正好是求和形式，也就是说拼接的时候虽然有先后顺序，但做完乘法就变成了无序的求和形式。

第一项中含有一个高阶tensor，假设一共有$m$种label，上式第一项的维度变化为：

$$(1\times k)(m\times k \times k)(k\times 1)=(m\times 1 \times 1)$$

结果

重新整理了一下作者的分数表格：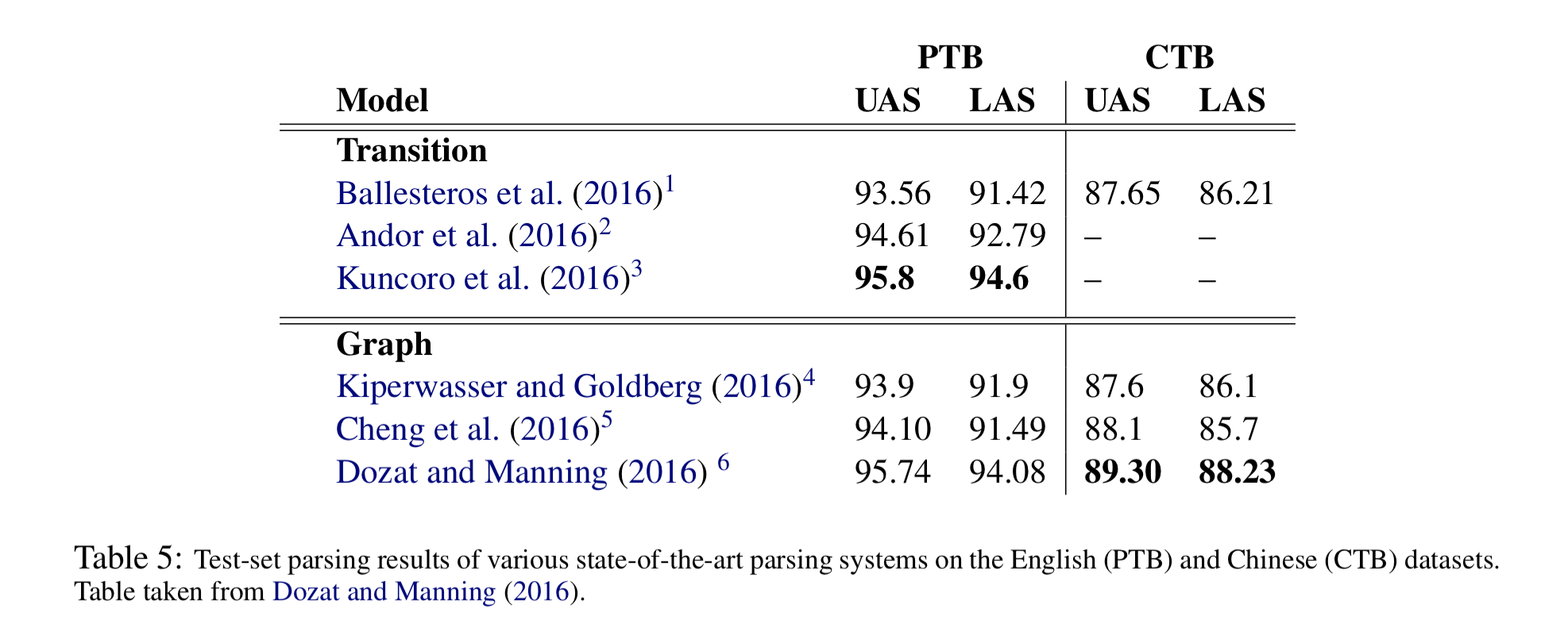

考虑到Kuncoro et al. (2016)的RNNG其实是用separately trained Generative Model去rerank另一个Discriminative Model sample到的100棵phrase structure树，占了ensemble的便宜，所以作者是过谦了。

代码

代码开源在：https://github.com/tdozat/Parser-v1

需要TensorFlow-0.10才能运行，比较古老：

# Linux
# export TF_BINARY_URL=https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-0.10.0-cp27-none-linux_x86_64.whl
# Mac
export TF_BINARY_URL=https://storage.googleapis.com/tensorflow/mac/cpu/tensorflow-0.10.0-py2-none-any.whl
pip install --upgrade $TF_BINARY_URL

另代码大量使用configparser传参，注释不多。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Deep Biaffine Attention for Neural Dependency Parsing