POJ 1912 A highway and the seven dwarfs 题解 《挑战程序设计竞赛》

POJ 1912 A highway and the seven dwarfs

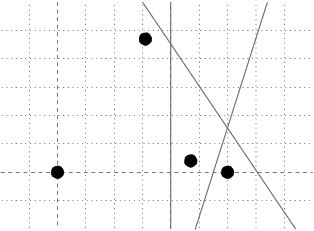
高铁与七个小矮人：侏儒岛上有N栋房子，组成一个社区。现给定一条高铁，问该高铁是否分割了社区？

3.6与平面和空间打交道的计算几何 

凸包 

不难想到这N个点里只有凸包才是关键，对于给定直线，将其视作向量，与原直线平行。那么与该向量成正角的点和成负角的点如果在直线两侧，则直线分割了凸包，否则不然。

另外，当只有一个点的时候需要特别考虑，否则会Runtime Error。

题目的测试数据可以在这里找到，比如下面这个例子就是个大杀器：

0
4 7 7 4
47 74 -3 3
47 74 -11 11

考虑了这点之后，代码美感稍有降低：

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;

#define MAX_N 100000 + 16
#define M_PI 3.14159265358979323846
#define EPS 1E-10

struct P
{
	double x, y;
	P() {}
	P(double x, double y) : x(x), y(y) {}
	P operator + (P p){ return P(x + p.x, y + p.y); }
	P operator - (P p){ return P(x - p.x, y - p.y); }
	P operator * (double d){ return P(x * d, y * d); }
	bool operator < (const P& a) const
	{
		if (x != a.x) return x < a.x;
		else return y < a.y;
	}
	double dot(P p) { return x*p.x + y*p.y; }
	double det(P p) { return x*p.y - y*p.x; }
};

// 求凸包
vector<P> convex_hull(P *ps, int N)
{
	sort(ps, ps + N);
	int k = 0;   // 凸包的顶点数
	vector<P> qs(N * 2);   // 构造中的凸包
	// 构造凸包的下侧
	for (int i = 0; i < N; ++i)
	{
		while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
		qs[k++] = ps[i];
	}
	// 构造凸包的上侧
	for (int i = N - 2, t = k; i >= 0; --i)
	{
		while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
		qs[k++] = ps[i];
	}
	qs.resize(k - 1);
	return qs;
}

P hs[MAX_N];
double as[MAX_N];	// 极角

inline double normalize(double r)
{
	if (r < -M_PI / 2.0 + EPS) r += M_PI * 2;
	return r;
}

inline double atan2(const P& p)
{
	return normalize(atan2(p.y, p.x));
}

inline bool double_cmp(double a, double b)
{
	return a + EPS < b;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int N;
	scanf("%d", &N);
	for (int i = 0; i < N; ++i) 
	{
		scanf("%lf%lf", &hs[i].x, &hs[i].y);
	}
	vector<P> chs;
	int n = 0;
	if (N > 1)
	{
		chs = convex_hull(hs, N);
		n = chs.size();
		chs.push_back(chs[0]);	// 将起点放进去，待会儿就可以不做求余了
	}
	
	for (int i = 0; i < n; ++i)
	{
		as[i] = atan2(chs[i + 1] - chs[i]);
	}
	sort(as, as + n, double_cmp);
	P p1, p2;
	while (~scanf("%lf%lf%lf%lf", &p1.x, &p1.y, &p2.x, &p2.y))
	{
		if (N < 2)
		{
			puts("GOOD");
			continue;
		}
		int i = upper_bound(as, as + n, atan2(p2 - p1), double_cmp) - as;// 直线两侧各找一点，若两点在直线两侧，则直线一定分割凸包
		int j = upper_bound(as, as + n, atan2(p1 - p2), double_cmp) - as;
		puts((((p2 - p1).det(chs[i] - p1) * (p2 - p1).det(chs[j] - p1) > -EPS)) ? "GOOD" : "BAD");
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1912 A highway and the seven dwarfs 题解 《挑战程序设计竞赛》