POJ 3608 Bridge Across Islands 题解 《挑战程序设计竞赛》

POJ 3608 Bridge Across Islands

跨岛大桥：在两个凸包小岛之间造桥，求最小距离？

3.6与平面和空间打交道的计算几何 

凸包 

这题原始数据已经是凸包（convex polygons）了，所以目的不是套Graham之类的凸包算法，而是包含在凸包算法中的旋转卡壳思想。如图：

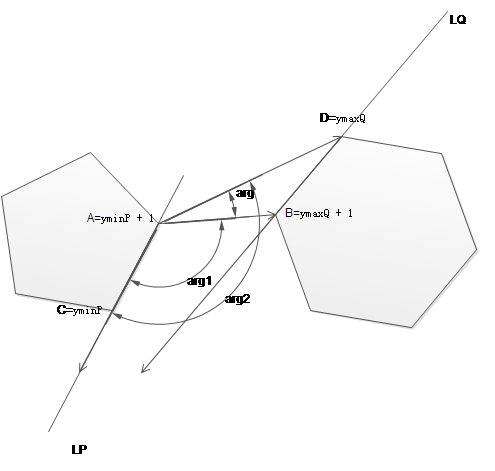
在P上找出最下方的点记作C，在Q上找最上方的点记作D，记C在逆时针方向的下一个顶点是A，同理定义B。那么我们得到了两个线段AC和DB，分别逆时针同时逐步旋转两线段，那么最短距离肯定在这两条线段上产生。

具体实现时，同时旋转体现为逐步选取逆时针方向上的下一个顶点作为C或D、A或B；两条线段的最短距离归结于四个顶点到另一线段的最短距离或直线的最短距离（平行），而点到线段的距离又归结于点到两个端点和点到直线（如果角度满足的话）的垂线距离，可见不平行的时候可以少考虑一种情况。

至于如何判断平行，代码中实际在用向量AC和DB的叉积判断两者是否平行。

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;

#define MAX_N 10000 + 16
#define INF 0x3F3F3F3F
#define EPS 1E-10

struct Point
{
	double x, y;
	Point() {}
	Point(double x, double y) : x(x), y(y) {}
	Point operator + (const Point& p){ return Point(x + p.x, y + p.y); }
	Point operator - (const Point& p){ return Point(x - p.x, y - p.y); }
	Point operator * (const double& d){ return Point(x * d, y * d); }
	bool operator < (const Point& a) const
	{
		if (x != a.x) return x < a.x;
		else return y < a.y;
	}
	double dot(const Point& p) { return x * p.x + y * p.y; }
	double det(const Point& p) { return x * p.y - y * p.x; }
};

Point P[MAX_N], Q[MAX_N];

// 向量AB 与 AC 的叉积 如果叉积大于0，那么C在向量AB的逆时针方向，叉积小于0则在AB的顺时针方向。如果叉积等于0，则ABC共线。
inline double cross(Point A, Point B, Point C)
{
	return (B - A).det(C - A);
}

// 向量AB 与 AC 的点积 如果点积的结果为0，那么这两个向量互相垂直
inline double multi(Point A, Point B, Point C)
{
	return (B - A).dot(C - A);
}

// 两点距离
inline double dist(Point A, Point B)
{
	return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}

// 逆时针排序
inline void anticlockwise_sort(Point* p, int N)
{
	for (int i = 0; i < N - 2; ++i)
	{
		double tmp = cross(p[i], p[i + 1], p[i + 2]);
		if (tmp > EPS) return;
		else if (tmp < -EPS)
		{
			reverse(p, p + N);
			return;
		}
	}
}

//计算C点到线段AB的最短距离
inline double point_to_line(Point A, Point B, Point C)
{
	if (dist(A, B) < EPS) return dist(B, C);
	if (multi(A, B, C) < -EPS) return dist(A, C);
	if (multi(B, A, C) < -EPS) return dist(B, C);
	return fabs(cross(A, B, C) / dist(A, B));
}

//求一条线段的两端点到另外一条线段的距离，反过来一样，共4种情况
inline double line_to_line(Point A, Point B, Point C, Point D)
{
	return min(min(point_to_line(A, B, C), point_to_line(A, B, D)), min(point_to_line(C, D, A), point_to_line(C, D, B)));
}

double solve(Point* P, Point* Q, int n, int m)
{
	int yminP = 0, ymaxQ = 0;
	for (int i = 0; i < n; ++i) if (P[i].y < P[yminP].y) yminP = i;	// P上y坐标最小的顶点
	for (int i = 0; i < m; ++i) if (Q[i].y > Q[ymaxQ].y) ymaxQ = i; // Q上y坐标最大的顶点
	P[n] = P[0];	// 为了方便，避免求余
	Q[m] = Q[0];
	double arg, ans = INF;
	for (int i = 0; i < n; ++i)
	{
		while (arg = cross(P[yminP + 1], Q[ymaxQ + 1], P[yminP]) - cross(P[yminP + 1], Q[ymaxQ], P[yminP]) > EPS) ymaxQ = (ymaxQ + 1) % m;
		ans = min(ans, line_to_line(P[yminP], P[yminP + 1], Q[ymaxQ], Q[ymaxQ + 1]));
		yminP = (yminP + 1) % n;
	}
	return ans;
}


///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int N, M;
	while (~scanf("%d%d", &N, &M) && N + M)
	{
		for (int i = 0; i < N; ++i)
		{
			scanf("%lf%lf", &P[i].x, &P[i].y);
		}
		for (int i = 0; i < M; ++i)
		{
			scanf("%lf%lf", &Q[i].x, &Q[i].y);
		}
		anticlockwise_sort(P, N);
		anticlockwise_sort(Q, M);
		printf("%.5lf\n", solve(P, Q, N, M));
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3608 Bridge Across Islands 题解 《挑战程序设计竞赛》