POJ 2079 Triangle 题解 《挑战程序设计竞赛》

POJ 2079 Triangle

凸包三角：求N个点组成的三角形的最大面积？

3.6与平面和空间打交道的计算几何 

凸包 

不难想到最大三角形一定由凸包的顶点构成，难点在于怎么搜索。O(N^3)枚举会超时，旋转卡壳法O(N^2)解决问题。

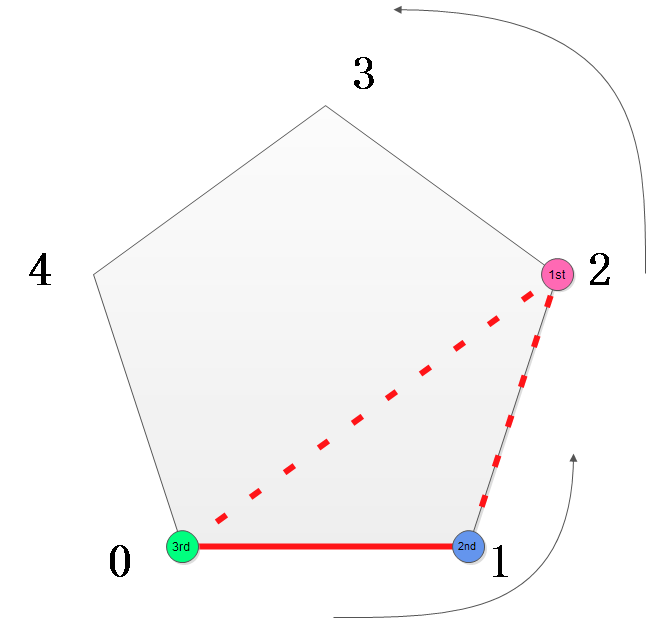
如图，先固定一条边（红色实线），然后搜索下一个顶点1st，三角形面积必然是先增后减的（极值在固定边的法线方向的最远点），一旦发现开始减小了，立即终止搜索，转而移动固定边。

固定边的移动也有讲究，固定边在顶点标号上的跨度用offset表示的话，offset不一定是1，最大可达到(N + 1)/2，于是将此offset也枚举一遍即可。

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

#define MAX_N 50000 + 16

typedef int type_xy;
struct Point
{
	type_xy x, y;
	Point() {}
	Point(type_xy x, type_xy y) : x(x), y(y) {}
	Point operator + (Point p){ return Point(x + p.x, y + p.y); }
	Point operator - (Point p){ return Point(x - p.x, y - p.y); }
	Point operator * (type_xy d){ return Point(x*d, y*d); }
	bool operator < (const Point& a) const
	{
		if (x != a.x) return x < a.x;
		else return y < a.y;
	}
	type_xy dot(Point p) { return x*p.x + y*p.y; }
	type_xy det(Point p) { return x*p.y - y*p.x; }
};

Point P[MAX_N];

// 向量AB 与 AC 的叉积 如果叉积大于0，那么C在向量AB的逆时针方向，叉积小于0则在AB的顺时针方向。如果叉积等于0，则ABC共线。
inline type_xy cross(Point A, Point B, Point C)
{
	return (B - A).det(C - A);
}

// AB和AC构成的平行四边形面积
inline type_xy compute_area(Point A, Point B, Point C)
{
	return abs(cross(A, B, C));
}

// 求凸包
vector <Point> convex_hull(Point *ps, int N)
{
	sort(ps, ps + N);
	int k = 0;   // 凸包的顶点数
	vector <Point> qs(N * 2);   // 构造中的凸包
	// 构造凸包的下侧
	for (int i = 0; i < N; ++i)
	{
		while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0)
			--k;
		qs[k++] = ps[i];
	}
	// 构造凸包的上侧
	for (int i = N - 2, t = k; i >= 0; --i)
	{
		while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0)
			--k;
		qs[k++] = ps[i];
	}
	qs.resize(k - 1);
	return qs;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int N;
	while (~scanf("%d", &N) && N > 0)
	{
		for (int i = 0; i < N; ++i)
		{
			scanf("%d%d", &P[i].x, &P[i].y);
		}

		vector <Point> ps = convex_hull(P, N);
		N = ps.size();
		int ans = 0;

		for (int offset = 1; offset < (N + 1) / 2; ++offset)
		{
			int first = (offset + 1) % N;
			for (int third = 0; third < N; ++third)
			{
				int second = (third + offset) % N;
				int prev = compute_area(ps[third], ps[second], ps[first]);
				for (++first; first != second && first != third; ++first)
				{
					if (first == N) first = 0;
					int cur = compute_area(ps[third], ps[second], ps[first]);
					ans = max(ans, prev);
					if (cur <= prev) break;	// 达到极值
					prev = cur;
				}
				--first;					// 退出循环时，其实first已经超了一个，这里减回来
				if (first == -1) first += N;
			}
		}

		printf("%d.%s\n", ans / 2, ans % 2 == 1 ? "50" : "00");
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2079 Triangle 题解 《挑战程序设计竞赛》