![]()

凸包游戏:N个点中去掉一个得到N个点集,求这些点集构成的凸包的最小面积?
3.6与平面和空间打交道的计算几何
凸包
不难想到去掉的点一定是凸包的顶点,于是就可以2000MS+水过去:
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
#define MAX_N 100000 + 16
typedef int type_xy;
typedef struct Point
{
int id;
type_xy x, y;
Point() {}
Point(type_xy x, type_xy y) : x(x), y(y) {}
Point operator + (Point p){ return Point(x + p.x, y + p.y); }
Point operator - (const Point& p){ return Point(x - p.x, y - p.y); }
Point operator * (type_xy d){ return Point(x*d, y*d); }
bool operator < (const Point& a) const
{
if (x != a.x) return x < a.x;
else return y < a.y;
}
type_xy dot(Point p) { return x*p.x + y*p.y; }
type_xy det(Point p) { return x*p.y - y*p.x; }
};
Point P[MAX_N], Q[MAX_N];
// 向量AB 与 AC 的叉积 如果叉积大于0,那么C在向量AB的逆时针方向,叉积小于0则在AB的顺时针方向。如果叉积等于0,则ABC共线。
inline type_xy cross(Point A, Point B, Point C)
{
return (B - A).det(C - A);
}
// AB和AC构成的平行四边形面积
inline type_xy compute_area(Point A, Point B, Point C)
{
type_xy res = cross(A, B, C);
if (res < 0)
{
return -res;
}
return res;
}
// 求多边形面积
inline type_xy compute_area(const vector<Point>& ps)
{
type_xy total = 0;
for (int i = 2; i < ps.size(); ++i)
{
total += compute_area(ps[0], ps[i - 1], ps[i]);
}
return total;
}
// 求凸包
vector <Point> convex_hull(Point *ps, int N)
{
sort(ps, ps + N);
int k = 0; // 凸包的顶点数
vector <Point> qs(N * 2); // 构造中的凸包
// 构造凸包的下侧
for (int i = 0; i < N; ++i)
{
while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
qs[k++] = ps[i];
}
// 构造凸包的上侧
for (int i = N - 2, t = k; i >= 0; --i)
{
while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
qs[k++] = ps[i];
}
qs.resize(k - 1);
return qs;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int N;
while (~scanf("%d", &N) && N > 0)
{
for (int i = 0; i < N; ++i)
{
scanf("%d%d", &P[i].x, &P[i].y);
P[i].id = i;
}
memcpy(Q, P, N * sizeof(Point));
vector<Point> ps = convex_hull(P, N);
type_xy ans = 0x3f3f3f3f;
for (int i = 0; i < ps.size(); ++i)
{
memcpy(P, Q, N * sizeof(Point));
swap(P[ps[i].id], P[N - 1]);
ans = min(ans, compute_area(convex_hull(P, N - 1)));
}
printf("%d.%s\n", ans / 2, ans % 2 == 1 ? "50" : "00");
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
| 13913068 | hankcs | 3246 | Accepted | 14264K | 2797MS | C++ | 2772B | 2015-02-25 23:32:05 |
我还有种思路,如图:
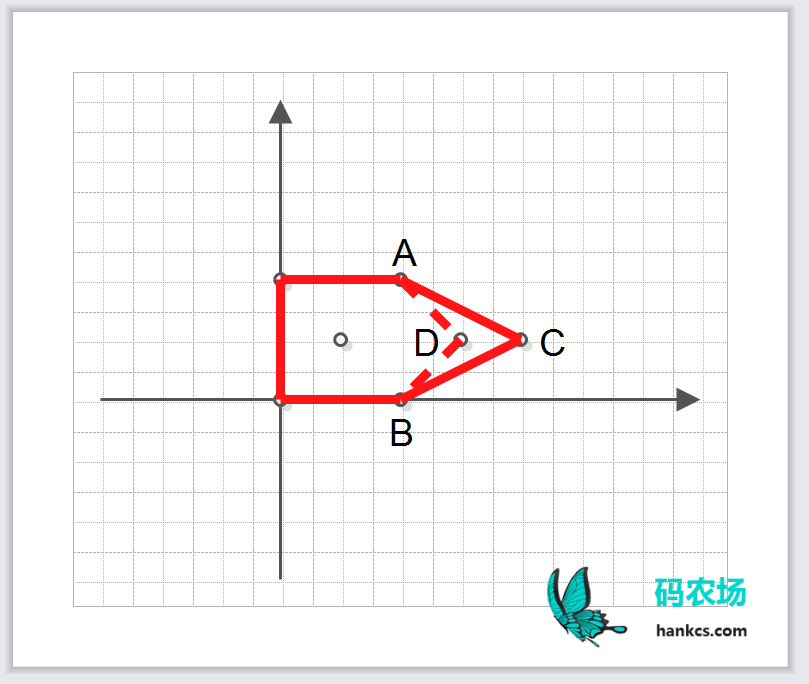
当去掉点C的时候,并不需要重新计算剩下的所有点构成的凸包。假设原凸包记作红色实线,去掉C后新凸包记作虚线。去掉C这个动作会产生两个效果:1、面积损失了三角形ABC这么大。2、如果ABC中还有点的话,面积增加这些点和AB构成的凸包面积。
不过最终一直WA,我也将这个思路和代码放在这里,留给各位聪明的读者斧正:
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
#define MAX_N 100000 + 16
typedef long long type_xy;
typedef struct Point
{
bool in_convex_hull;
type_xy x, y;
Point() {}
Point(type_xy x, type_xy y) : x(x), y(y) {}
Point operator + (Point p){ return Point(x + p.x, y + p.y); }
Point operator - (const Point& p){ return Point(x - p.x, y - p.y); }
Point operator * (type_xy d){ return Point(x*d, y*d); }
bool operator < (const Point& a) const
{
if (x != a.x) return x < a.x;
else return y < a.y;
}
type_xy dot(Point p) { return x*p.x + y*p.y; }
type_xy det(Point p) { return x*p.y - y*p.x; }
};
Point P[MAX_N], Q[MAX_N];
// 向量AB 与 AC 的叉积 如果叉积大于0,那么C在向量AB的逆时针方向,叉积小于0则在AB的顺时针方向。如果叉积等于0,则ABC共线。
inline type_xy cross(Point A, Point B, Point C)
{
return (B - A).det(C - A);
}
// AB和AC构成的平行四边形面积
inline type_xy compute_area(Point A, Point B, Point C)
{
type_xy res = cross(A, B, C);
if (res < 0)
{
return -res;
}
return res;
}
// 求多边形面积
inline type_xy compute_area(const vector<Point>& ps)
{
type_xy total = 0;
for (int i = 2; i < ps.size(); ++i)
{
total += compute_area(ps[0], ps[i - 1], ps[i]);
}
return total;
}
// 求凸包
vector <Point> convex_hull(Point *ps, int N, bool tag = false)
{
sort(ps, ps + N);
int k = 0; // 凸包的顶点数
vector <Point> qs(N * 2); // 构造中的凸包
// 构造凸包的下侧
for (int i = 0; i < N; ++i)
{
while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
if (tag) ps[i].in_convex_hull = true;
qs[k++] = ps[i];
}
// 构造凸包的上侧
for (int i = N - 2, t = k; i >= 0; --i)
{
while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
if (tag) ps[i].in_convex_hull = true;
qs[k++] = ps[i];
}
qs.resize(k - 1);
return qs;
}
inline int nxt(const int& i, const int& N)
{
if (i + 1 < N) return i + 1;
return 0;
}
inline int pre(const int& i, const int& N)
{
if (i - 1 >= 0) return i - 1;
return N - 1;
}
//判断点M,N是否在直线AB的同一侧
inline bool is_point_at_same_side_of_line( Point pointM, Point pointN,
Point pointA, Point pointB)
{
return cross(pointA, pointB, pointM) * cross(pointA, pointB, pointN) > 0;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int N;
while (~scanf("%d", &N) && N > 0)
{
for (int i = 0; i < N; ++i)
{
scanf("%d%d", &P[i].x, &P[i].y);
P[i].in_convex_hull = false;
}
vector <Point> ps = convex_hull(P, N, true);
int ans = 0x3f3f3f3f;
int total_area = compute_area(ps);
for (int i = 0; i < ps.size(); ++i)
{
Point A = ps[pre(i, ps.size())];
Point B = ps[nxt(i, ps.size())];
Point C = ps[i];
int triangle = compute_area(C, A, B);
int size = 0;
for (int j = 0; j < N; ++j)
{
Point D = P[j];
if (!D.in_convex_hull && is_point_at_same_side_of_line(C, D, A, B))
{
Q[size++] = D;
}
}
Q[size++] = A;
Q[size++] = B;
int mini_area = 0;
if (size >= 3)
{
vector <Point> ps_mini = convex_hull(Q, size);
mini_area = compute_area(ps_mini);
}
ans = min(ans, total_area - triangle + mini_area);
}
printf("%d.%s\n", ans / 2, ans % 2 == 1 ? "50" : "00");
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
 码农场
码农场