POJ 3728 The merchant​ 题解《挑战程序设计竞赛》

POJ 3728 The merchant 

游吟商人：N个城市同种商品价格不同，任意两个城市间有且仅有一条简单路径。请快速计算商人在指定两点的路线上做一次买卖所能赚到的最大利润。

4.3成为图论大师之路 

LCA

中国人出的英文题目总是让人误解，从来不从读者的角度考虑，很多隐含的限制都没有表达出来。比如载货量等于1等。

先考虑最简单的情况熟悉熟悉数据，如果只在相邻两个城市间买卖，价格差带来的收益注明在边上，题目的示例数据处理后如图：

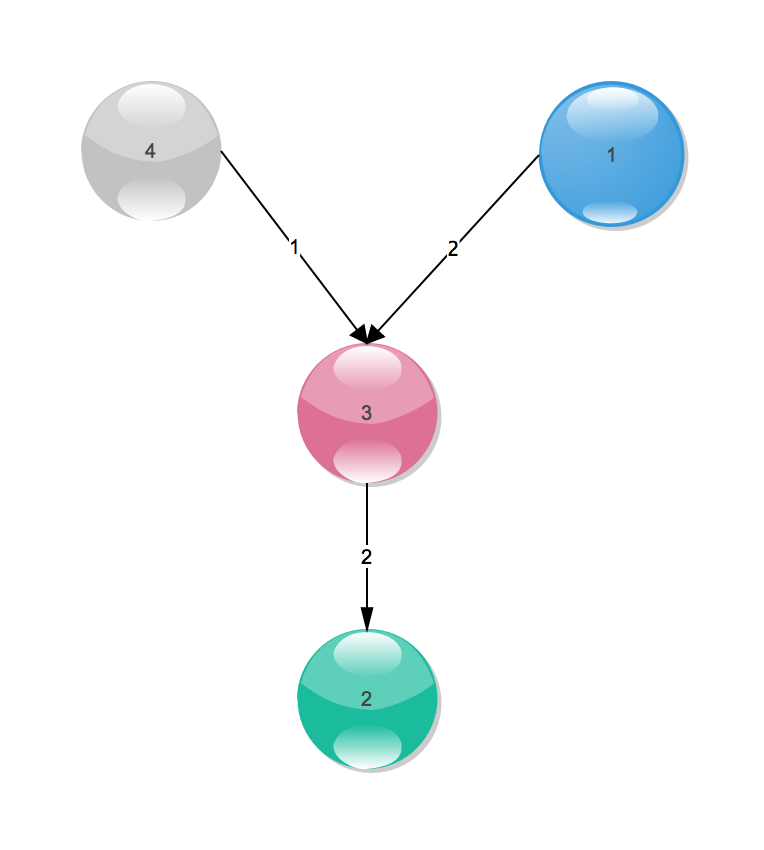
若买卖不在相邻城市，朴素的想法是遍历找出路径，然后找出路径上的最高最低价格得到价格差。然而每次光找路径就要耗费O(n)的时间，而题目中肯定有多个Query。

用动态规划的思路解决问题，对指定两点uv，假设v往上走2^k步的父节点为t，走2^(k+1)步的父节点为u，如下图所示

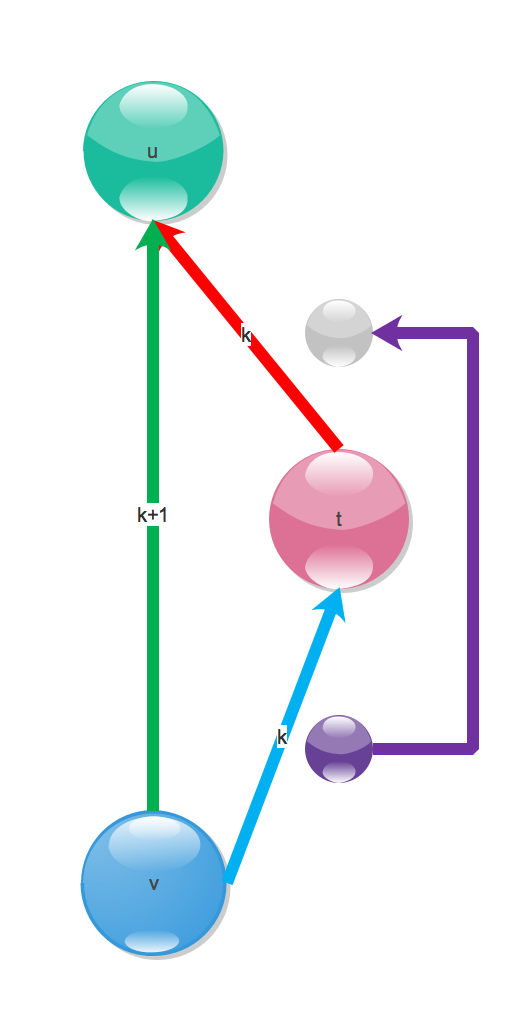
边上的数字表示深度之差。

定义四个dp数组：

int dp_max[MAX_LOG_V][MAX_V], dp_min[MAX_LOG_V][MAX_V]; // 往上走2^k步之间的最高与最低价格
int dp_up[MAX_LOG_V][MAX_V], dp_down[MAX_LOG_V][MAX_V]; // [从v往上走2^k步之间]或[往下走2^k步到v之间]相应的最大利润

前两个很好计算，对于uv的dp_up，买卖事件有3种情况：

• 买和卖都发生在ut之间

• 买和卖都发生在tv之间

• 买和卖分别发生在ut和tv之间

所以递推公式如下

dp_up[k + 1][v] = max(max(dp_up[k][v], dp_up[k][t]), dp_max[k][t] - dp_min[k][v]);

同理有dp_down。

预处理算出这4个dp数组后，对任意uv，取t=lca，用类似的思想分成3种情况（对于前两种情况有down和up的子分支），取最大值即可。

#include <iostream>
#include <vector>

using namespace std;

#define MAX_V 50000
#define MAX_LOG_V 16

// 输入
vector<int> G[MAX_V];  // 图的邻接表表示
int price[MAX_V];

int parent[MAX_LOG_V][MAX_V];  // 向上走2^k步所到的节点（超过根时记为-1）
int depth[MAX_V];              // 节点的深度

int dp_max[MAX_LOG_V][MAX_V], dp_min[MAX_LOG_V][MAX_V]; // 往上走2^k步之间的最高与最低价格
int dp_up[MAX_LOG_V][MAX_V], dp_down[MAX_LOG_V][MAX_V]; // [从v往上走2^k步之间]或[往下走2^k步到v之间]相应的最大利润

void dfs(int v, int p, int d)
{
    parent[0][v] = p;
    depth[v] = d;
    dp_up[0][v] = max(price[p] - price[v], 0);
    dp_down[0][v] = max(price[v] - price[p], 0);
    dp_max[0][v] = max(price[v], price[p]);
    dp_min[0][v] = min(price[v], price[p]);
    for (int i = 0; i < G[v].size(); i++)
    {
        if (G[v][i] != p)
            dfs(G[v][i], v, d + 1);
    }
}

// 预处理
void init(int V)
{
    memset(dp_max, 0, sizeof dp_max);
    memset(dp_min, 0x3f, sizeof dp_min);
    // 预处理出parent[0]和depth
    dfs(0, -1, 0);
    // 预处理出parent
    for (int k = 0; k + 1 < MAX_LOG_V; k++)
    {
        for (int v = 0; v < V; v++)
        {
            if (parent[k][v] < 0)
                parent[k + 1][v] = -1;
            else
            {
                parent[k + 1][v] = parent[k][parent[k][v]];
                int t = parent[k][v];
                dp_max[k + 1][v] = max(dp_max[k][v], dp_max[k][t]);
                dp_min[k + 1][v] = min(dp_min[k][v], dp_min[k][t]);
                dp_up[k + 1][v] = max(max(dp_up[k][v], dp_up[k][t]), dp_max[k][t] - dp_min[k][v]);
                dp_down[k + 1][v] = max(max(dp_down[k][v], dp_down[k][t]), dp_max[k][v] - dp_min[k][t]);
            }

        }
    }
}

// 计算u和v的LCA
int lca(int u, int v)
{
    // 让u和v向上走到同一深度
    if (depth[u] > depth[v])
        swap(u, v);
    for (int k = 0; k < MAX_LOG_V; k++)
    {
        if ((depth[v] - depth[u]) >> k & 1)
        {
            v = parent[k][v];
        }
    }
    if (u == v)
        return u;
    // 利用二分搜索计算LCA
    for (int k = MAX_LOG_V - 1; k >= 0; k--)
    {
        if (parent[k][u] != parent[k][v])
        {
            u = parent[k][u];
            v = parent[k][v];
        }
    }
    return parent[0][u];
}

void add_edge(int u, int v)
{
    G[u].push_back(v);
}

/**
 * 从 x 向上走 2^k 步能够得到的最大利润以及经过城市的最低价格
 * @param x 
 * @param k 
 * @param min_price 
 * @return 最大利润
 */
int up(int x, int k, int &min_price)
{
    min_price = 0x3f3f3f3f;
    int max_profit = 0;
    int prev_min_price = 0x3f3f3f3f;
    for (int i = MAX_LOG_V - 1; i >= 0; i--)
    {
        if (k >> i & 1)
        {
            min_price = min(min_price, dp_min[i][x]);
            max_profit = max(max_profit, dp_up[i][x]);
            max_profit = max(max_profit, dp_max[i][x] - prev_min_price);
            prev_min_price = min(prev_min_price, dp_min[i][x]);
            x = parent[i][x];
        }
    }
    return max_profit;
}

/**
 * 向下走 2^k 步走到 x 能够得到的最大利润以及经过城市的最高价格
 * @param x 
 * @param k 
 * @param max_price 
 * @return 最大利润
 */
int down(int x, int k, int &max_price)
{
    max_price = 0;
    int max_profit = 0;
    int pre_max_price = 0;
    for (int i = MAX_LOG_V - 1; i >= 0; i--)
    {
        if (k >> i & 1)
        {
            max_price = max(max_price, dp_max[i][x]);
            max_profit = max(max_profit, dp_down[i][x]);
            max_profit = max(max_profit, pre_max_price - dp_min[i][x]);
            pre_max_price = max(pre_max_price, dp_max[i][x]);
            x = parent[i][x];
        }
    }
    return max_profit;
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    int N;
    scanf("%d", &N);
    for (int i = 0; i < N; ++i)
    {
        scanf("%d", price + i);
    }
    for (int i = 0; i < N - 1; i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        --u, --v;
        add_edge(u, v);
        add_edge(v, u);
    }
    init(N);
    int Q;
    scanf("%d", &Q);
    while (Q--)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        --u, --v;
        int LCA = lca(u, v);
        int max_price, min_price;
        int up_profit = up(u, depth[u] - depth[LCA], min_price);
        int down_profit = down(v, depth[v] - depth[LCA], max_price);
        int ans = max(max(up_profit, down_profit), max_price - min_price);
        printf("%d\n", ans);
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3728 The merchant​ 题解《挑战程序设计竞赛》