POJ 1986 Distance Queries​ 题解《挑战程序设计竞赛》

POJ 1986 Distance Queries 

LCA距离：快速查询树中任意两个节点间的最短距离。

4.3成为图论大师之路 

LCA

也就是两个节点到最近公共祖先的距离之和，求出每个节点到根节点的距离之后，uv两点间距离=d[u]+d[v]-2*d[lca]。

LCA可以用RMQ快速实现：

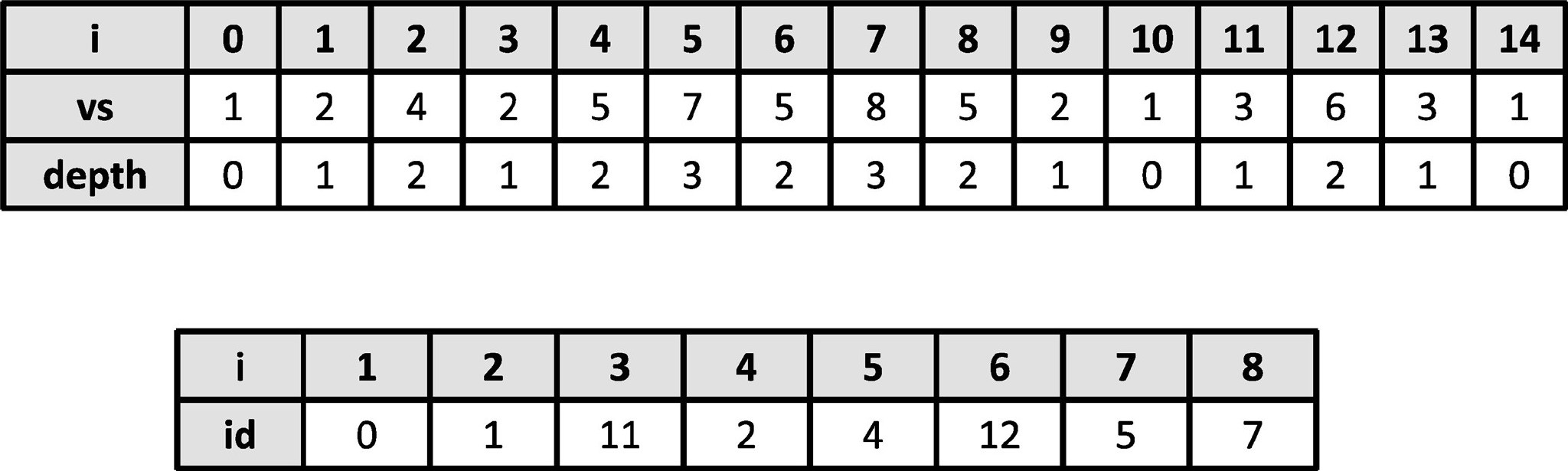
对于涉及有根树的问题，将树转为从根DFS标号后得到的序列处理的技巧常常十分有效。对于LCA，利用该技巧也能够高效地计算。首先，按从根DFS访问的顺序得到顶点序列vs[i]和对应的深度depth[i]。对于每个顶点v，记其在vs中首次出现的下标为id[v]。

这些都可以在O(n)时间内求得。而LCA(u,v)就是访问u之后到访问v之前所经过顶点中离根最近的那个，假设id[u]≤id[v]，那么有

LCA(u,v)=vs[id[u]≤i≤id[v]中令depth(i)最小的i。

而这可以利用RMQ高效地求得。

另外这题其实是书上例题POJ 2763的劣化版，因为不需要修改通过路径的weight，所以不必按照书上那样链式展开

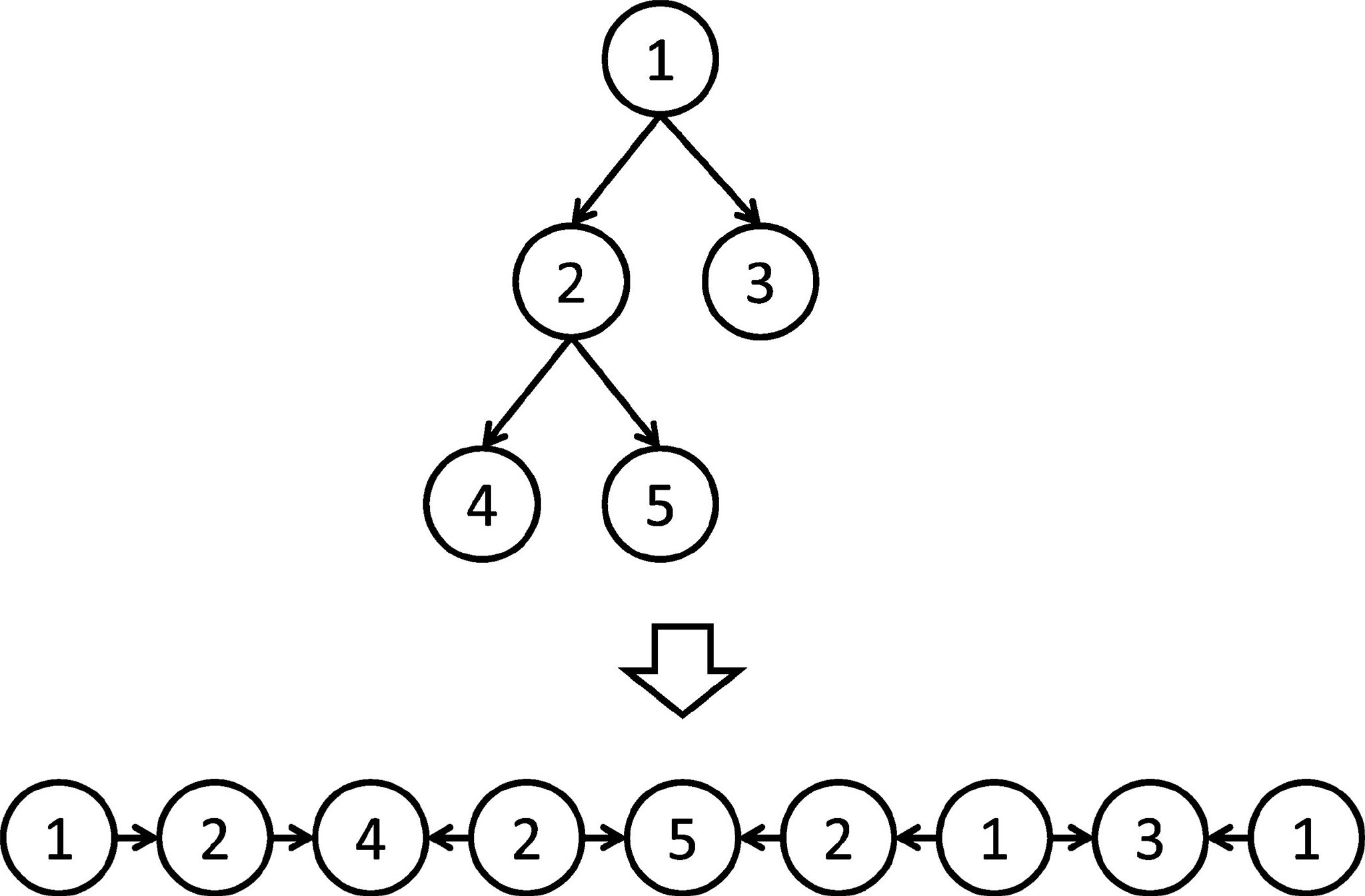
直接dfs得到d，然后lca做加减法即可。

#include <iostream>
#include <vector>

using namespace std;

#define MAX_V 40000
#define MAX_LOGV 16

struct edge
{
    int to, weight;
    edge(int to, int weight) : to(to), weight(weight) {}
};
vector<edge> G[MAX_V];     // 图的邻接表表示
int vs[MAX_V * 2 - 1];     // DFS访问的顺序
int depth[MAX_V * 2 - 1];  // 节点的深度
int id[MAX_V];             // 各个顶点在vs中首次出现的下标
int dist[MAX_V];           // 节点到根节点的距离

int bit[MAX_V * 2 - 1][MAX_LOGV];  // RMQ的BinaryIndexedTree节点

/**
 * 初始化RMQ
 * @param n 节点个数
 */
void rmq_init(int n)
{
    for (int i = 0; i < n; i++)
    {
        bit[i][0] = i;
    }
    for (int j = 1; (1 << j) < n; j++)
    {
        for (int i = 0; i + (1 << j) - 1 < n; i++)
        {
            if (depth[bit[i][j - 1]] <= depth[bit[i + (1 << (j - 1))][j - 1]])
            {
                bit[i][j] = bit[i][j - 1];
            }
            else
            {
                bit[i][j] = bit[i + (1 << (j - 1))][j - 1];
            }
        }
    }
}

/**
 * 查询[l, r)之间的最小值对应的下标
 * @param l
 * @param r
 * @return
 */
int query(int l, int r)
{
    int k = 0;
    while ((1 << (k + 1)) < r - l + 1)
        k++;
    if (depth[bit[l][k]] <= depth[bit[r - (1 << k)][k]])
    {
        return bit[l][k];
    }
    else
    {
        return bit[r - (1 << k)][k];
    }
}

void dfs(int v, int p, int d, int &k)
{
    id[v] = k;
    vs[k] = v;
    depth[k++] = d;
    for (int i = 0; i < G[v].size(); i++)
    {
        if (G[v][i].to != p)
        {
            dist[G[v][i].to] = dist[v] + G[v][i].weight;
            dfs(G[v][i].to, v, d + 1, k);
            vs[k] = v;
            depth[k++] = d;
        }
    }
}

// 预处理
void init(int V)
{
    // 预处理出vs、depth和id
    int k = 0, root = 0;
    dfs(root, -1, 0, k);
    // 预处理出RMQ（返回的不是最小值，而是最小值对应的下标）
    rmq_init(V * 2 - 1);
}

// 计算u和v的LCA
int lca(int u, int v)
{
    return vs[query(min(id[u], id[v]), max(id[u], id[v]) + 1)];
}

void add_edge(int from, int to, int weight)
{
    G[from].push_back(edge(to, weight));
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    int V, E;
    while (~scanf("%d %d", &V, &E))
    {
        int u, v, w;
        char r;

        for (int i = 0; i < E; ++i)
        {
            scanf("%d%d%d %c", &u, &v, &w, &r);
            --u, --v;
            add_edge(u, v, w);
            add_edge(v, u, w);
        }
        init(V);
        int K;
        scanf("%d", &K);
        for (int i = 0; i < K; ++i)
        {
            int u, v;
            scanf("%d%d", &u, &v);
            --u, --v;
            int t = lca(u, v);
            int ans = dist[u] - dist[t] + dist[v] - dist[t];
            printf("%d\n", ans);
        }
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1986 Distance Queries​ 题解《挑战程序设计竞赛》