目录

3.1 基本概念
3.1.1 图
无向图、有向图、连通图和回路。
3.1.2 树
森林:无回路无向图。
树:无回路连通无向图。
根树:有根节点的树。
3.1.3 字符串
Σ:是字符表。
字符串:由Σ中字符相连而成的有限序列被称之为Σ 上的字符串(或称符号串,或称链)。
空串:特殊地,不包括任何字符的字符串称为空串,记作ε。
字符串长度:符号串中符号的个数。符号串x的长度用|x|表示。|ε| = 0。
Σ*:包括空串在内的Σ上的全部字符串。
字符串连接:xy=把y的各个符号写在x的符号之后得到的符号串。
xn:把x自身连接n次得到的符号串,即z=xx…x (n个x), 称为x的n次方幂,记作xn。
字符串集合乘积:将来自两个字符串的集合的字符串按顺序连接起来。
闭包运算:字符表Σ上的所有可能的字符串组成一个集合V。
正闭包:V+ = V* – {ε},即闭包减去空串。
3.2 形式语言
3.2.1 概述
3.2.2 形式语法的定义
形式语法:形式语法是一个4元组G=(N, Σ, P, S), 其中N 是非终结符(通常大写,如A、B)的有限集合;Σ是终结符(通常小写,如x、a、b)的有限集合,N ∩ Σ = Φ;V = N ∪ Σ 称总词汇表;P 是一组重写规则的有限集合:P={ α → β },其中,α,β 是V 中元素构成的串,但α 中至少应含有一个非终结符号;S ∈ N,称为句子符或初始符。这有点像编译原理?编程语言就是自然语言的模型……吧。
推导:β->γ表示αβγ可以转换到αδγ,这种转换记作![]()
按非平凡方式派生:![]() 表示至少推导一次。
表示至少推导一次。
派生:![]() 表示推导0或正数次。
表示推导0或正数次。
最左推导:每步推导中只改写最左边的那个非终结符。
最右推导:每步推导中只改写最右边的那个非终结符,也称规范推导。
句子:由初始符按照重写规则推导出来的句子形式。其中不含非终结符的句子形式称为G 生成的句子。
语言:由文法G 生成所有句子,记作L(G)。![]()
3.2.3 形式语法的类型
分为4种类型:3、2、1、0型文法,分别对应:
1.正则文法
正则文法:所有规则均推导出开头或结尾为终结字符的字串(自己理解的)。如果文法G=(N, Σ, P, S) 的P 中的规则满足如下形式:A → B x,或A → x,其中A, B ∈ N,x ∈ Σ,则称该文法为正则文法(简写为FSG)或称3型文法(左线性正则文法)。(如果A → x B,则该文法称为右线性正则文法。)
2.上下文无关文法
上下文无关文法:所有规则的左侧和推导结果不限于N或Σ,其实就是正则文法阉割掉限制。如果P 中的规则满足如下形式:A → α,其中A ∈ N,α ∈ (N ∪ Σ)*,则称该文法为上下文无关文法(CFG)或称2 型文法。
3.上下文有关文法
推导规则左右侧的不同之处体现在字串的中间,就是生活常识里的上下文相关了。如果P 中的规则满足如下形式: α A β → α γ β,其中A ∈ N,α, β, γ ∈ (N ∪ Σ)*,且γ 至少包含一个字符,则称该文法为上下文有关文法(CSG)或称1 型文法。
规则左侧不一定仅仅是一个N,并且右侧一定不短于左侧。
4.无约束文法
无约束文法:正闭包中的字串推导出闭包字串。如果P 中的规则满足如下形式: α → β,α, β 是字符串,则称G 为无约束文法,或称0型文法。
总结
文法的编号体现了文法的约束程度之大,L(G0) ⊇ L(G1) ⊇ L(G2) ⊇ L(G3)。文法类型取决于全部规则中编号最小的那一种。
3.2.4 CFG 产生的语言句子的派生树表示
自己理解的是按照S在左侧的规则从大到小拆成树,这让我想起了现代汉语课上的短语类型分析。
二义性文法:一个文法G对应两颗或以上的分析树。比如“关于鲁迅的文章”。
3.3 自动机理论
自动机是概念上的演算机器。
3.3.1 有限自动机
确定性有限自动机:
确定的有限自动机(Definite Automata, DFA) M 是一个五元组:
M = (Σ, Q, δ, q0, F)
其中,
Σ 是输入符号的有穷集合;
Q 是状态的有限集合;
δ 是Q 与Σ 的直积Q × Σ 到Q (下一个状态) 的映射。它支配着有限状态控制的行为,有时也称为状态转移函数。
q0 ∈ Q 是初始状态;
F 是终止状态集合,F ⊆ Q;
我觉得可以把DFA想象成一个单放机,插入一盘磁带,随着磁带的转动,DFA读取一个符号,依靠状态转移函数改变自己的状态,同时磁带转到下一个字符。
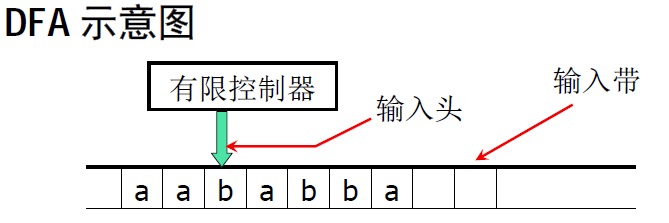
不确定的有限自动机:
(Non-definite Automata, NFA)不确定的有限自动机M 是一个五元组
M = (Σ, Q, δ, q0, F)
其中,
Σ 是输入符号的有穷集合;
Q 是状态的有限集合;
δ 是Q与Σ的直积Q×Σ 到Q的幂集2Q 的映射。
F 是终止状态集合,F ⊆ Q;
q0 ∈ Q 是初始状态;
两者的不同在于,DFA接受一个符号之后的状态是唯一的,而NFA则是一个集合中的某个。
NFA接受的语言:如果存在一个状态p,有p∈δ(q0,x)且p∈F,则称句子x被NFA M所接受。被M接受的句子的集合称为NFA M定义的语言,记作T(M)。
NFA 与DFA 的关系:设L 是一个被NFA 所接受的句子的集合,则存在一个DFA,它能够接受L 。(用数学归纳法很好证明)
3.3.2 正则文法与有限自动机的关系
一定存在一个FA可以定义正则文法的语言:若G = (VN, VT, P, S ) 是一个正则文法,则存在一个有限自动机M = (Σ, Q, δ, q0, F),使得:T(M) = L(G)。
FA M的构造方法,M = (Σ, Q, δ, q0, F)
Σ为G的Σ
Q为G的N和{T}的并集(T是一个概念上虚拟的非终止符,代表一个终止状态)
如果P中有产生式B->a,则加入将T加入映射δ(B,a),如果P中有产生式B->aC,则将C加入映射δ(B,a)。最后对每一个终止符a∈VT δ(T,a) = ∅
q0毫无疑问为S
如果P中有产生式S->e(初始直接终结)则F={S,T}(将S看做终止状态)否则F={T}。
一定存在一个正则文法可以定义FA的语言:若M = (Σ, Q, δ, q0, F) 是一个有限自动机,则存在正则文法G = (VN, VT, P, S ) 使L(G)=T(M)。
3.3.3 上下文无关文法与下推自动机
PDA:下推自动机(Push-Down Automata, PDA)可以表达成一个7元组:
M = (Σ, Q, Γ, δ, q0, Z0, F)
其中,
Σ 是输入符号的有穷集合;
Q 是状态的有限集合;
Γ 为下推存储器符号的有穷集合;
δ 是从Q×(Σ∪{ε})×Γ 到Q×Γ* 的子集的映射。
q0 ∈ Q 是初始状态;
Z0∈Γ 为最初出现在下推存储器顶端的开始符号;
F 是终止状态集合,F ⊆ Q;
映射关系δ(q, a, Z) = {(q1, γ1), (q2, γ2), …, (qm, γm)}表示当前状态q,接受字符a,自动机可能进入状态qi,并且栈顶符号弹出,γm入栈。没看出来这个概念有什么用,也没看出来跟上下文无关文法有什么关系。
图灵机和线性界限自动机似乎更加看不出来有什么用处,老毛病又犯了,你不告诉我它有什么用,我就不学它。万一它真的有用,我随时再学就行了。
3.4 自动机在自然语言处理中的应用
3.4.1 单词拼写检查
关于有限自动机找出正确字串,修改图的深度优先搜索算法即可,弄个stack,注意剪枝就行。
3.4.2 单词形态分析
有限状态转换机:(finite state transducer, FST)粗略地讲,有限状态转换机与有限自动机(或有限状态机)的区别在于:FST在完成状态转移的同时产生一个输出,而FA(或FSM)只实现状态转移,不产生任何输出。
在达到状态heav的时候,再接受y的话结束,再接受i的时候输出heavy同时接受空输入,接着输出+然后接受后缀er或est等等。
3.4.3 词性消歧
其实我看完之后觉得这丫就是个Tire树吧……
第三章读后感
概念很多,如果不准备搞学术的话千万不要看;否则千万要整理个重点出来,不然看不懂论文。实际工业生产中很多司空见惯的东西在学术上有种种“学名”,懂一点总是好的,至少可以以学名作为关键字上Google查资料或者问别人。
以后可能不会写这样的博文了,因为公式太难打了……正在考虑买个Note,用SPen写笔记的话应该挺不错。正巧没有手机用,买个3G的Note 2014 Edition还能打电话。可惜国产的TD-SCDMA总是不被国外认可,导致我的移动卡不能上3G 。
。
 码农场
码农场