CS224n笔记9 机器翻译和高级LSTM及GRU

简单回顾了传统统计机器翻译中的难题，过渡到利用GRU和LSTM来救场，最后介绍了一些较新的改进工作。

机器翻译

对于情感分析这类还算简单的任务，你可以整理一个情感极性词典、编写一堆规则做出一个勉强能用的系统。但到了机器翻译这个高级应用，就无法完全依靠规则了。现代机器翻译手段都是基于统计的，在平行语料上学习语言知识。世界上第一个平行语料库是罗塞塔石碑：

图片来源：wiki

传统机器翻译系统非常复杂，因为不同阶段用到了不同的机器学习方法。

传统统计机器翻译系统

定义一些符号：

原文$f$

译文$e$

机器翻译定义为找到使如下条件概率最大的$e$：

$$\hat{e}=\text{argmax}_ep(e|f)=\text{argmax}_ep(f|e)p(e)$$

这里利用了贝叶斯公式。翻译模型$p(f|e)$在平行语料上训练得到，语言模型$p(e)$在未对齐的原文语料上训练（是非常廉价的）。

公式描述的翻译过程如下：

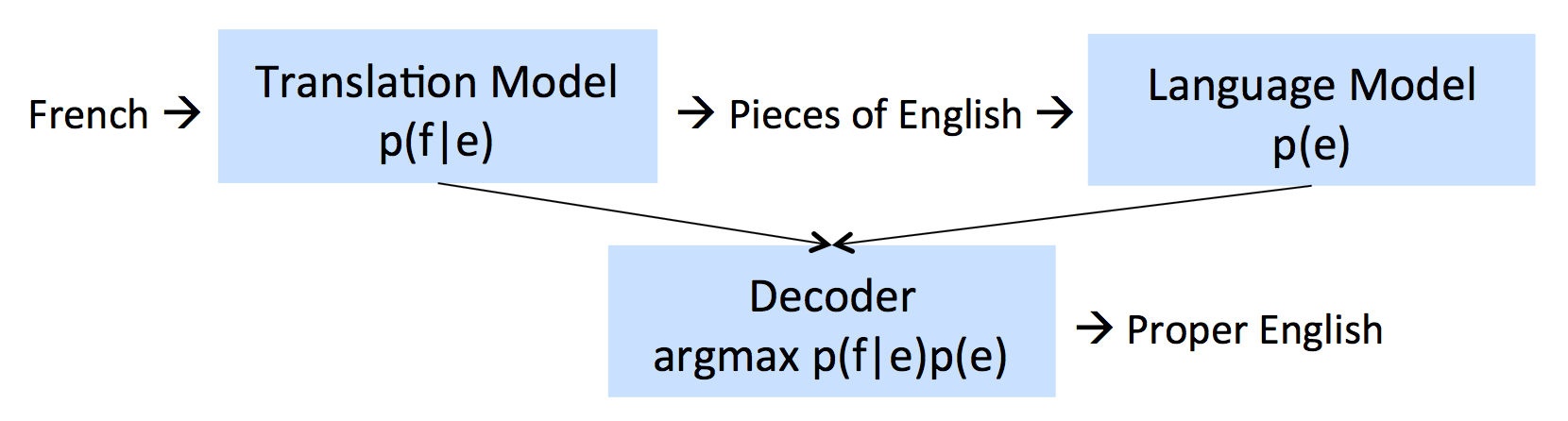
第一步：对齐

找到原文中的哪个句子或短语翻译到译文中的哪个句子或短语，这个第一步已经够难了。

对齐时，原文中可能有部分词语没有对应的译文：

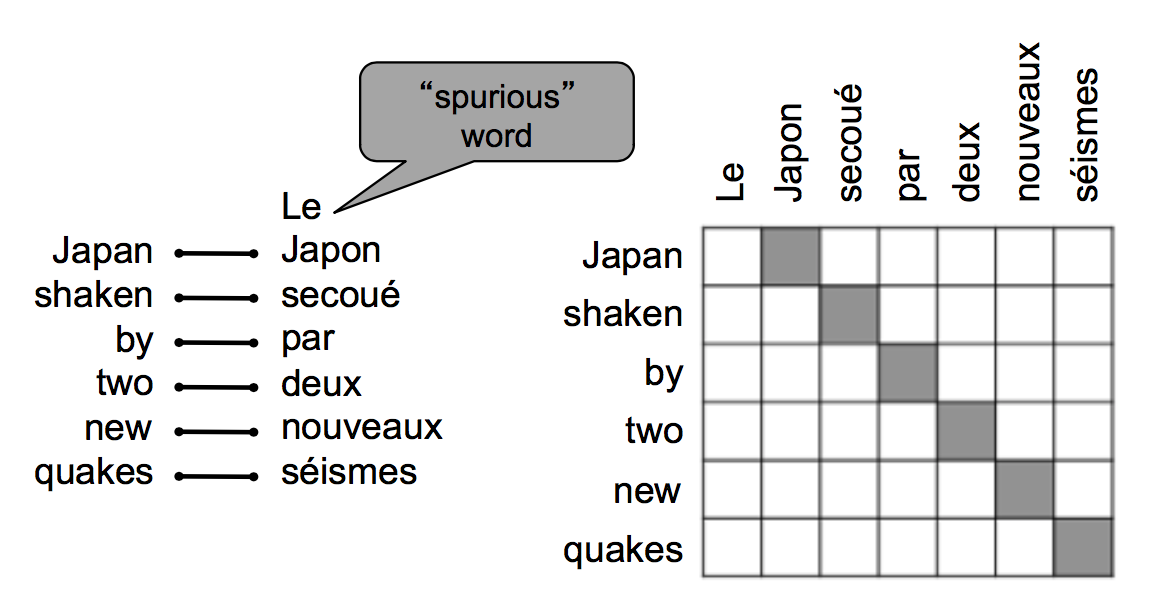
也可能在译文中有部分词语没有对应的原文，根据模型不同，可能有一对多的对齐方式：

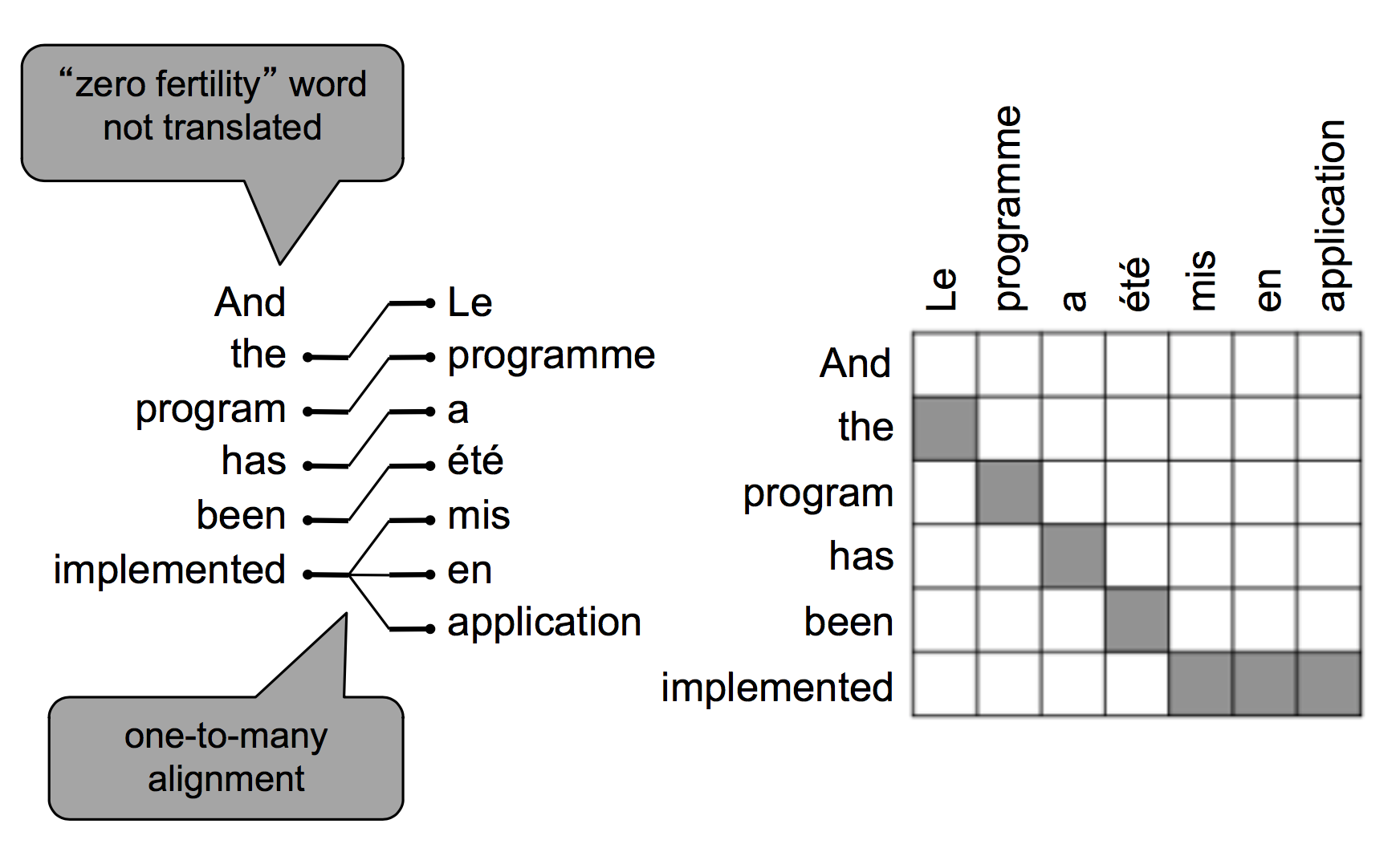
也可能有多对一的对齐方式：

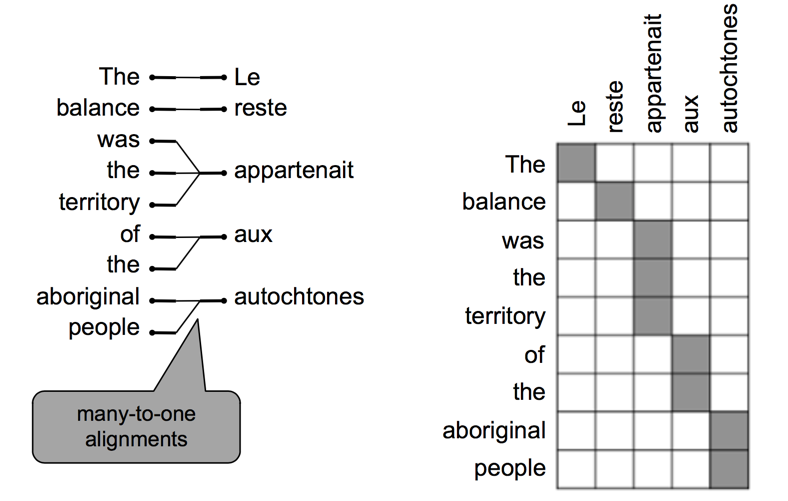
还可能有多对多的对齐方式：

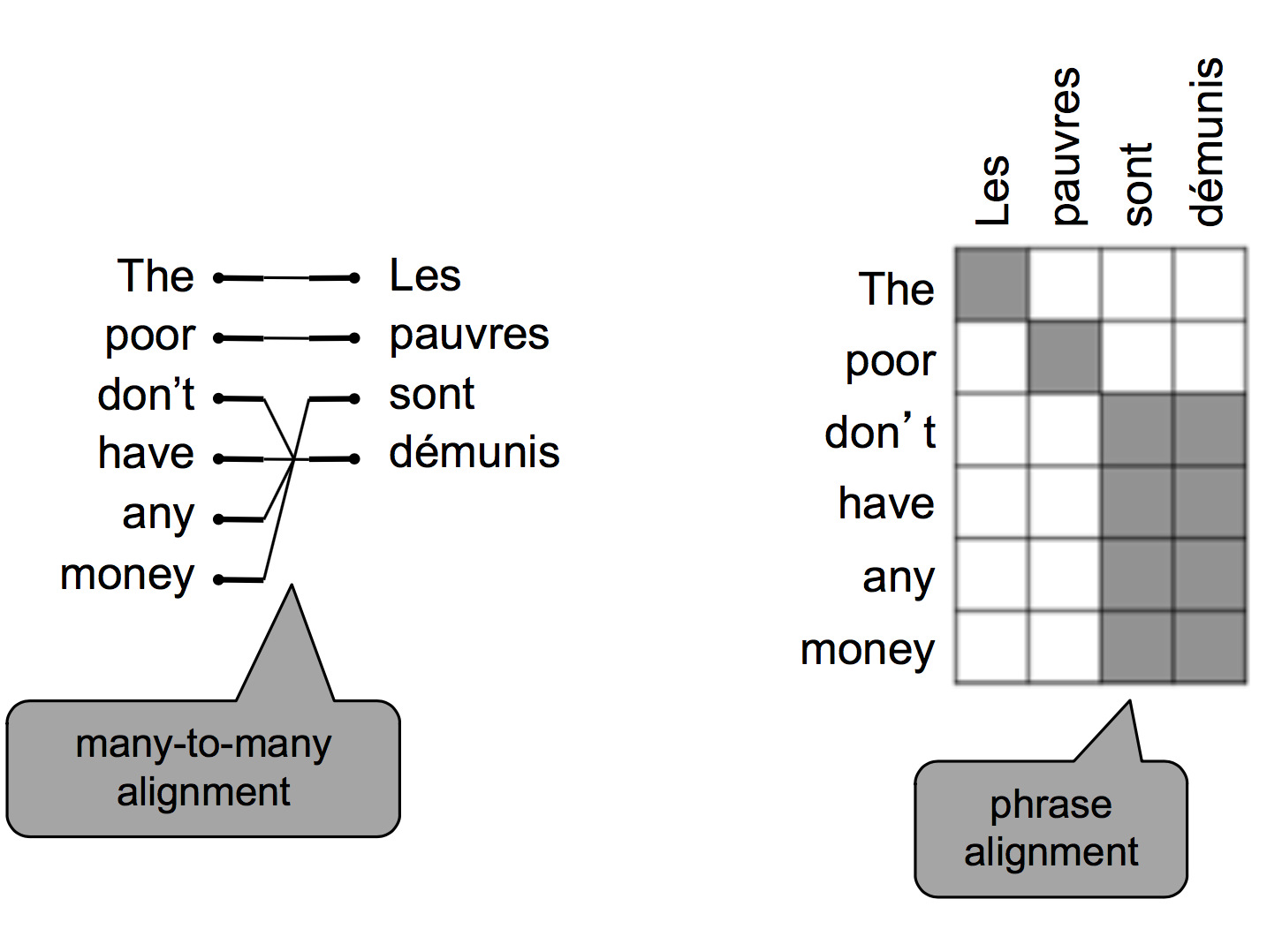
所有的对齐方式数量是组合数级的。

有时候还要通过句法分析，来进行不同颗粒度的对齐：

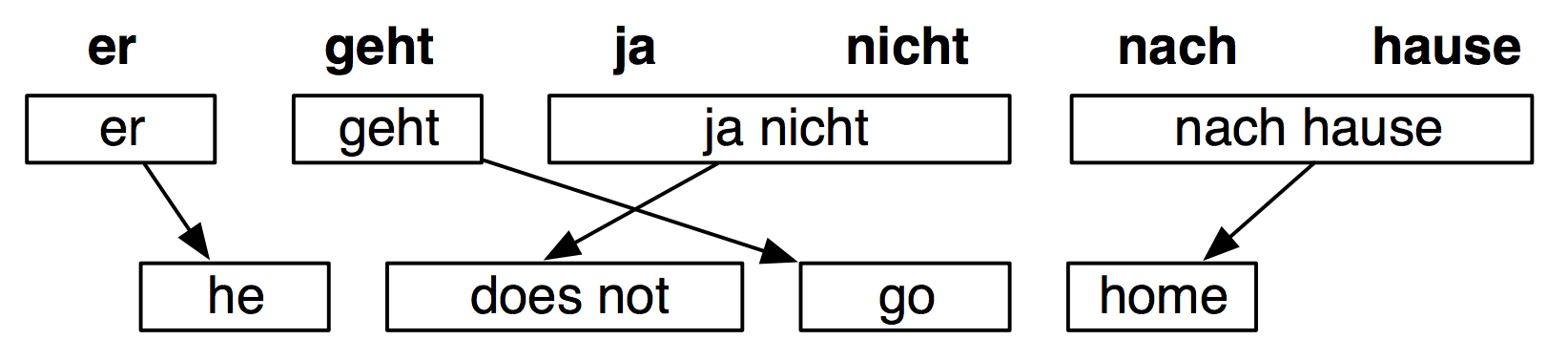
对齐之后

原文中每个单词都有多个备选单词，导致了许多短语的组合方式：

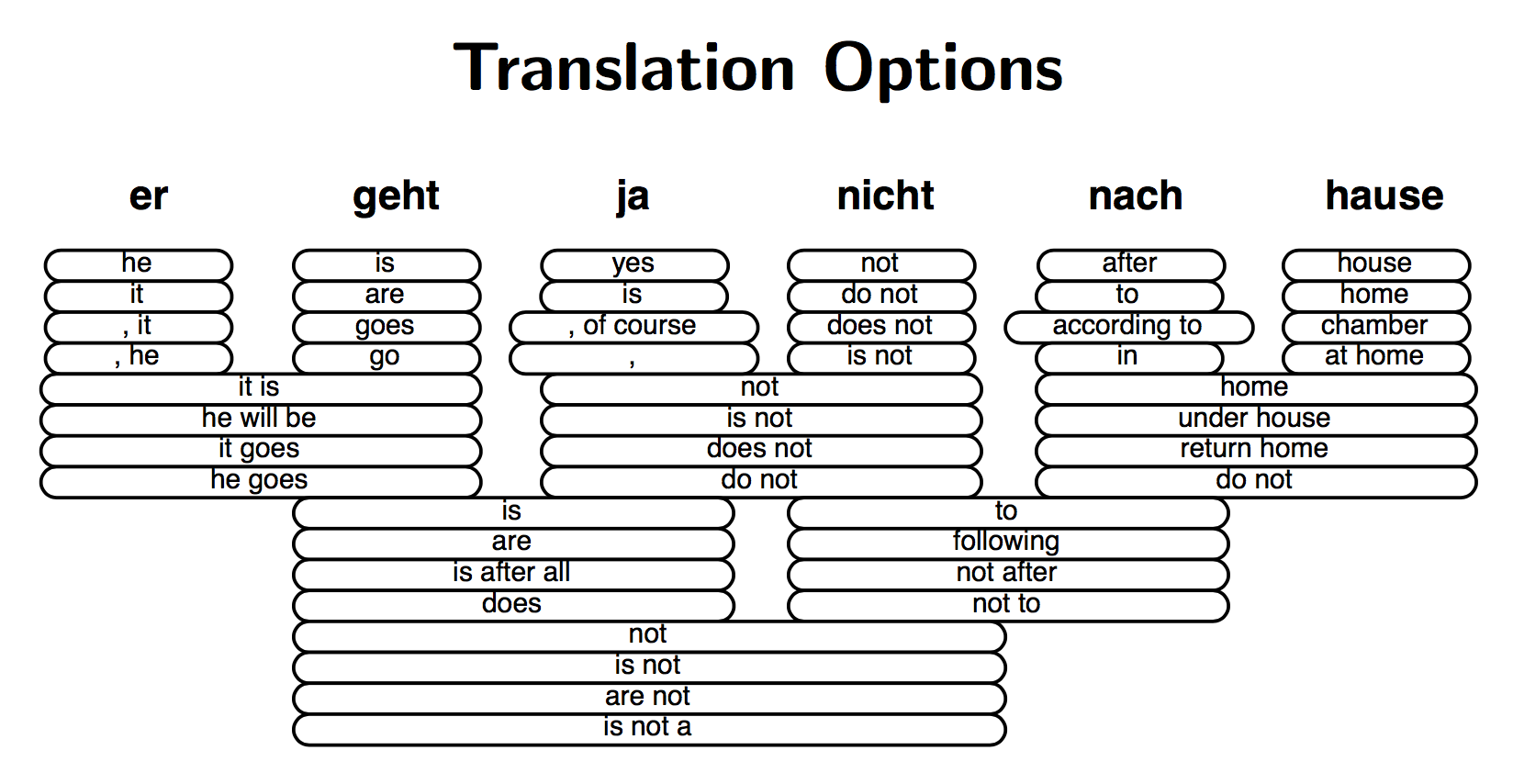
解码：在海量假设中搜索最佳选择

这是一个特别复杂的搜索问题，涉及到许多语言模型。

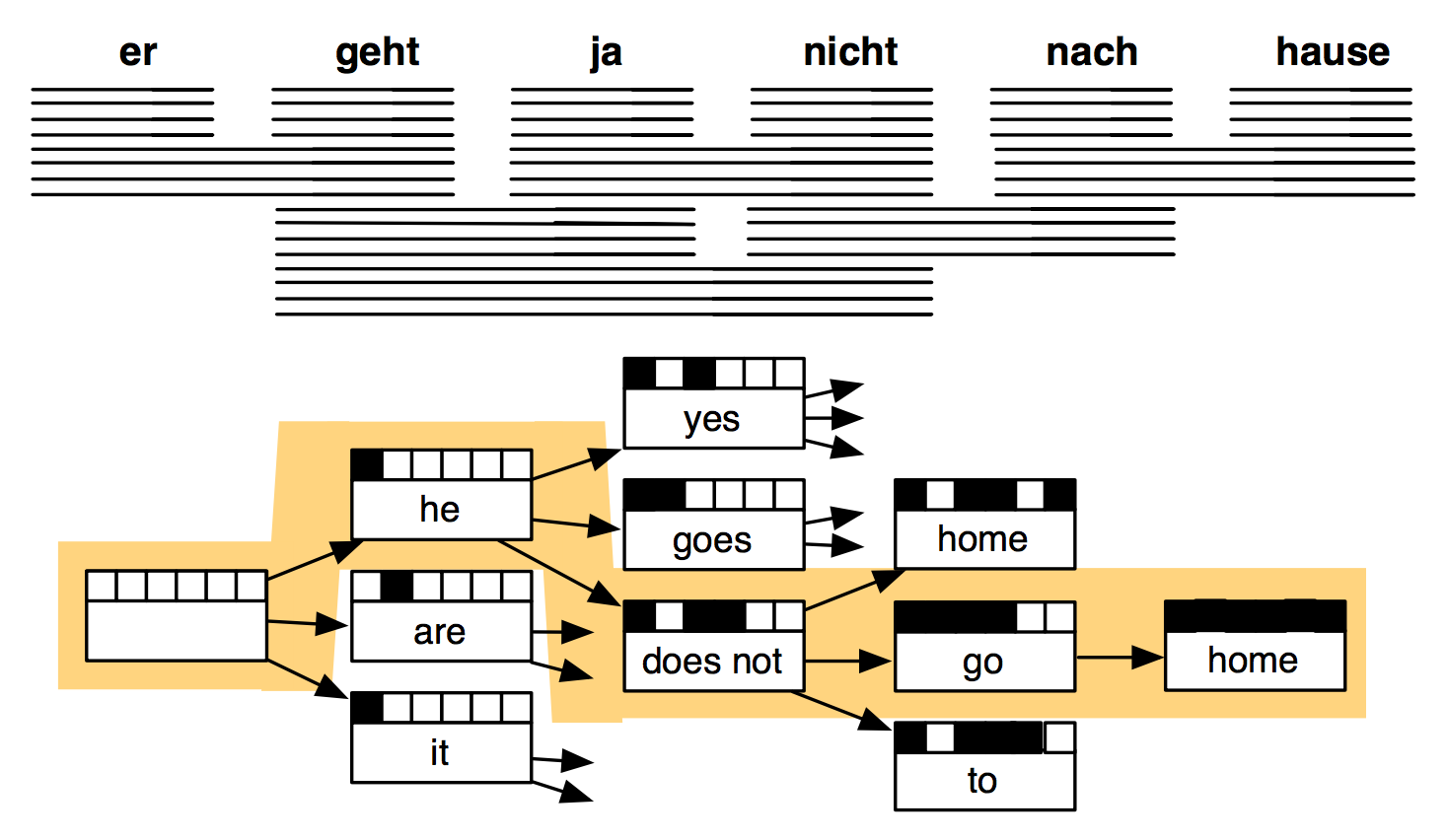
传统机器翻译

这还只是传统机器翻译系统的冰山一角，有许多细节没有涉及到，还需要大量的人肉特征工程，总之是非常复杂的系统。其中每个环节都是独立不同的机器学习问题。这些独立的模型各自为政，并不以一个统一的优化目标为最终目标。

而深度学习则提供了一个统一的模型，一个统一的最终目标函数。在优化目标函数的过程中，得到一个end to end的完整的joint模型。传统机器翻译系统与深度学习是截然相反的，对齐模型、词序模型、语言模型……一堆独立的模型无法联合训练。

深度学习来救场

也许可以直接用RNN来接受原文，预测译文“下一个单词”：

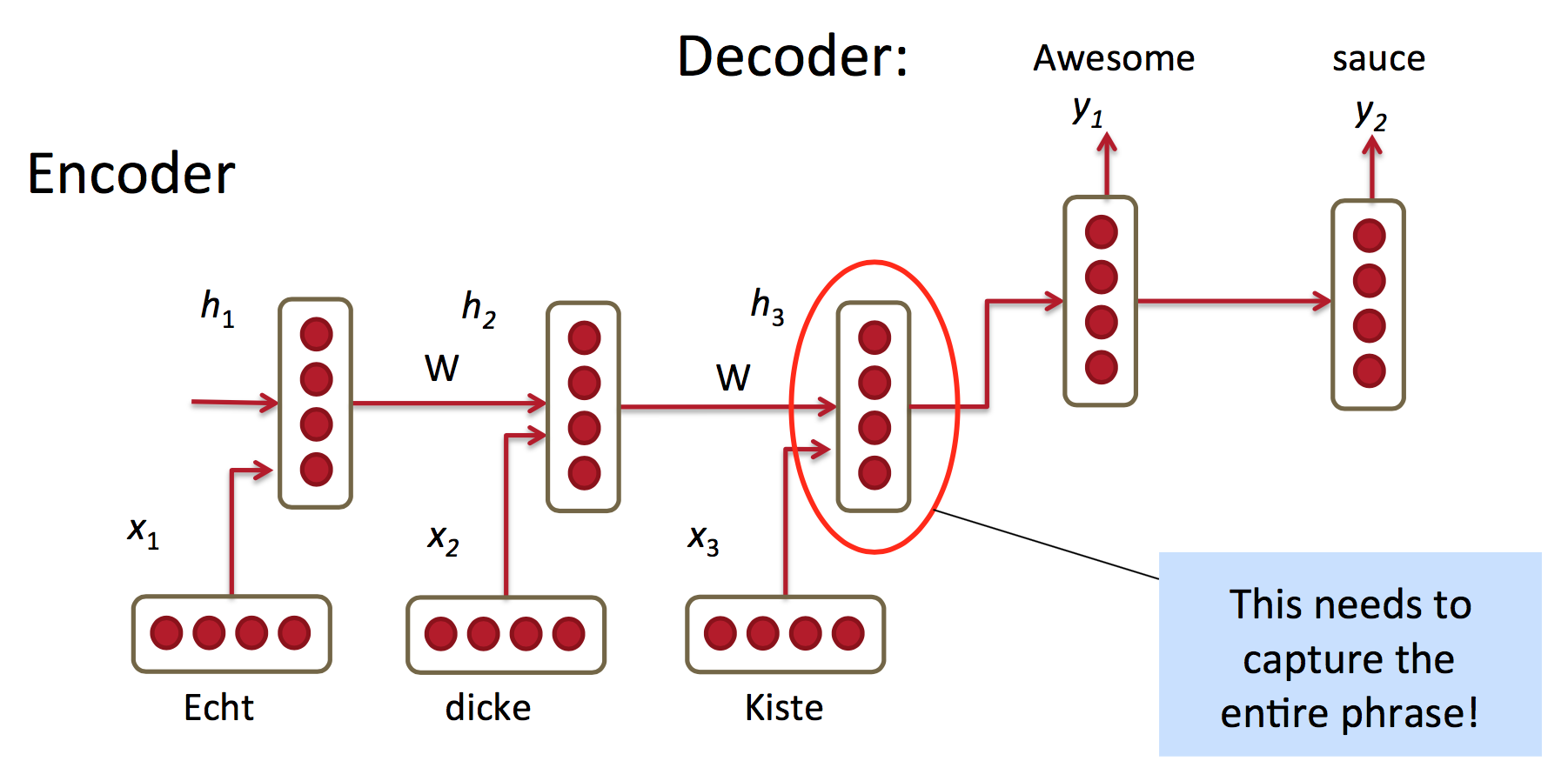
红圈所示特征表示必须能捕捉整个原文短语的语义，但是RNN无法记住太久之前的事情，大概五六个单词就到极限了。所以这不是个实用的模型。

在这个最简单的模型中，

Encoder是：

$$\begin{equation} h_t = \phi (h_{t-1}, x_t) = f (W^{(hh)} h_{t-1} + W^{(hx)} x_t) \end{equation}$$

Decoder是：

$$\begin{equation} h_t = \phi (h_{t-1}) = f (W^{(hh)} h_{t-1}) \end{equation}$$

$$\begin{equation}y_t = softmax (W^{(S)}h_t)\end{equation}$$

最小化所有训练实例上的交叉熵误差：

$$\begin{equation}\max_{\theta} \dfrac {1}{N} \sum_{n=1}^{N} \log p_{\theta} (y^{(n)}|x^{(n)})\end{equation}$$

记号 $\phi(v_1,v_2)$ 一般代表接受的两个向量的权值不同。

softmax分类器中必须有个代表句子终止的“单词”，不然模型会无休止地输出下去。

但神经网络机器翻译模型没有这么简单，必须加一些拓展。

1、编码器和解码器训练不同的权值矩阵

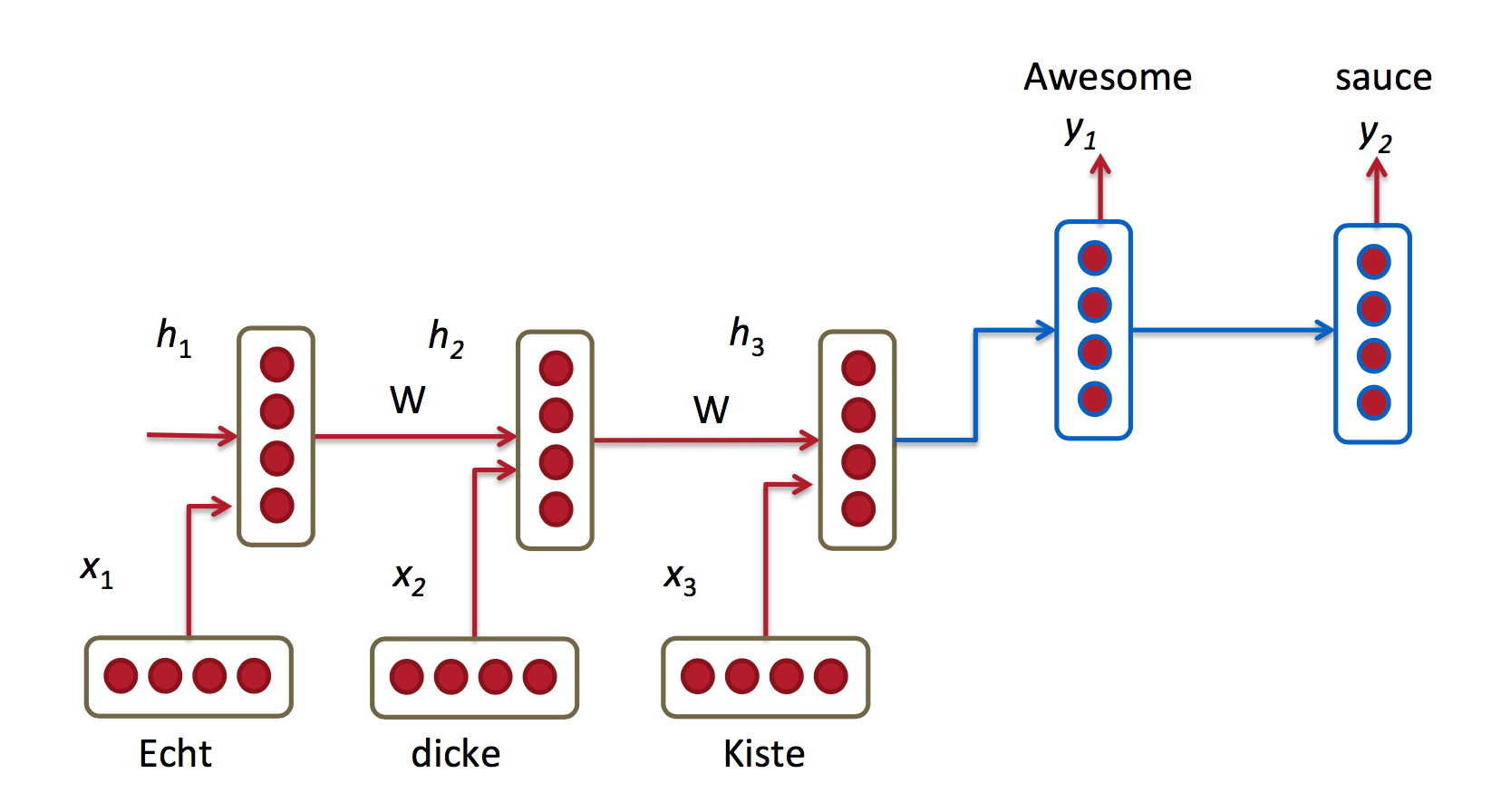
红蓝代表不同的权值。

2、decoder中的隐藏层的输入来自3个方面：

• 前一个时刻的隐藏层

• encoder的最后一个隐藏层($c = h_T$)

• 前一个预测结果 $\hat{y}_{t-1}$

  这样导致decoder函数变为：

  $$\begin{equation} h_{t} = \phi (h_{t-1}, c, y_{t-1}) \end{equation}$$

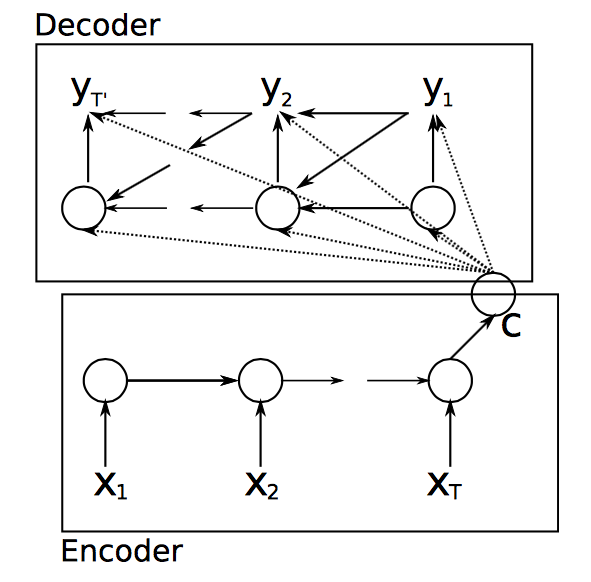
这可以辅助训练softmax的权值矩阵，防止模型重复生成同一个单词。

上图还有一个复杂版本，表达的是同一个意思：

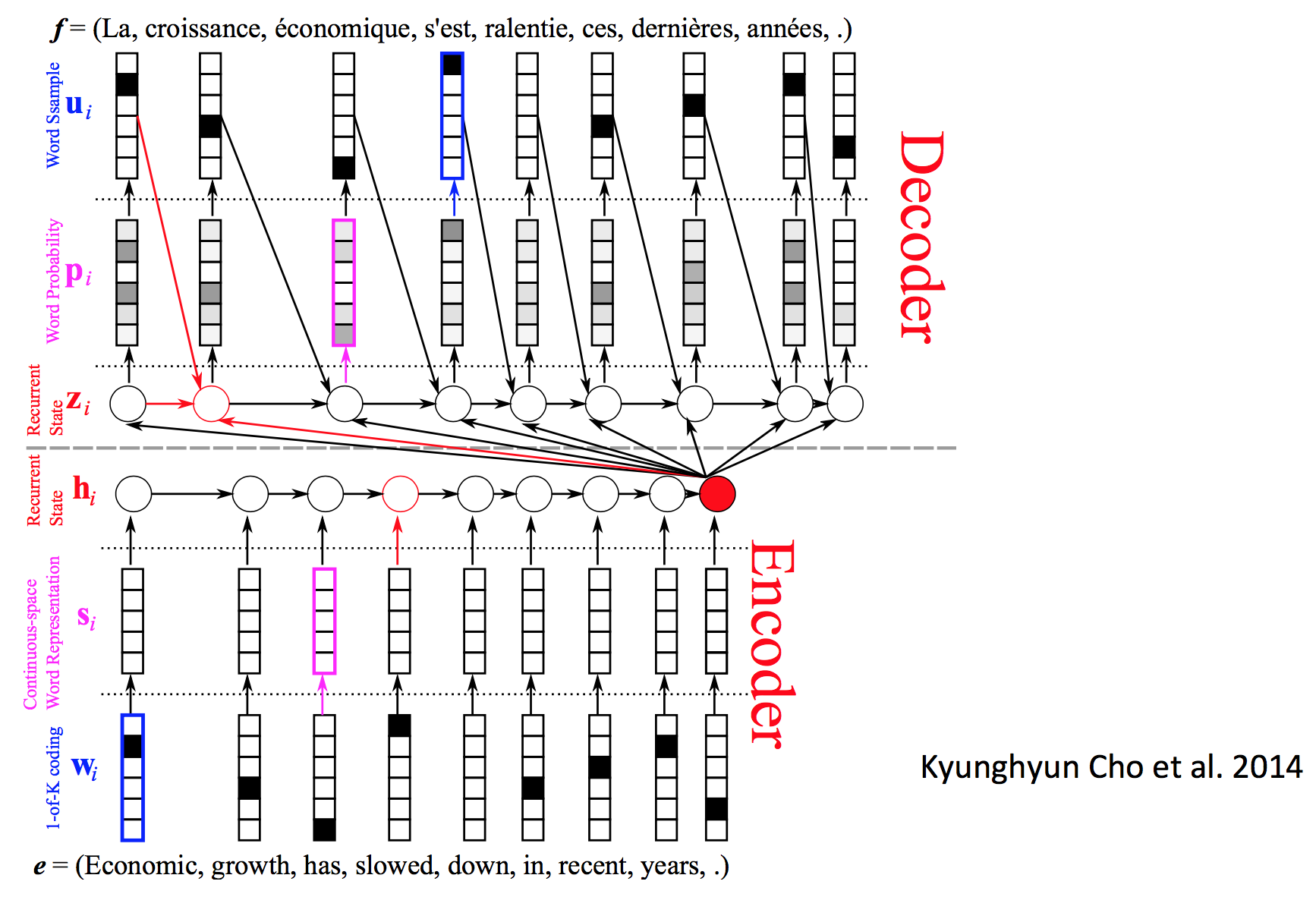
其中，带黑点的表示离散的向量表示，否则表示连续的向量空间。

3、使用深度RNN

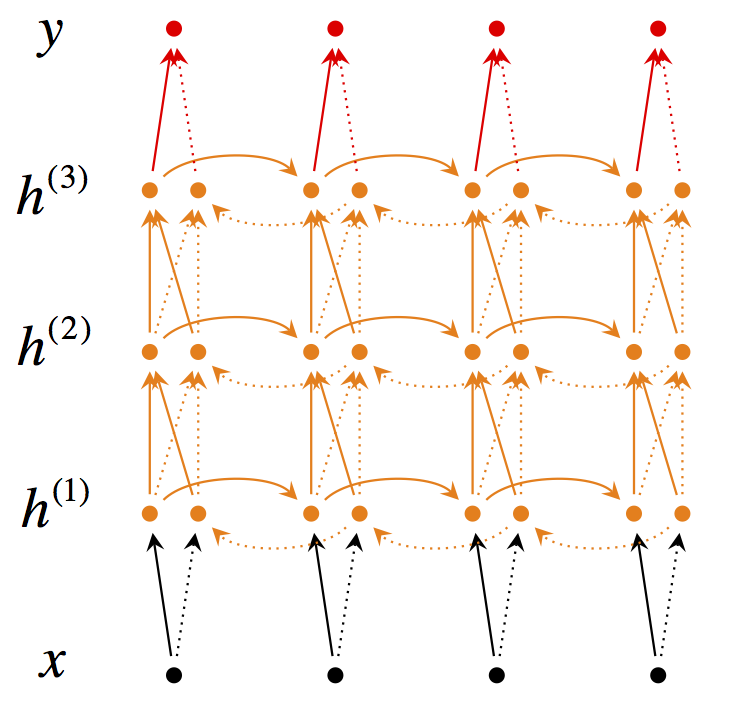
4、使用 bi-directional encoder

5、不再用$\textit{A B C} \to \textit{X Y}$作为训练实例，而是逆转原文词序：$\textit{C B A} \to \textit{X Y}$。因为A更可能翻译为X，而梯度消失导致A无法影响输出，倒过来A离输出近一些。逆转词序不会带来“语法语义上的改变”，因为模型学习的就是如何从逆序的原文翻译顺序的译文。但相应的，C就离Y更远了

主要改进：更好的单元

引入Gated Recurrent Units (GRU)，这种单元可以让模型学习何时遗忘从而将记忆保持很久、允许误差根据输入的不同而不同。

标准的RNN直接计算隐藏层：

$$h_t = \sigma(W^{(hh)} h_{t-1} + W^{(hx)} x_{t})$$

GRU先根据当前输入的词向量和隐藏层计算一个update gate（另一个层）：

$$z_t=\sigma\left(W^{(z)}x_t+U^{(z)}h_{t-1}\right)$$

利用相同的方法不同的权值计算reset gate

$$r_t=\sigma\left(W^{(r)}x_t+U^{(r)}h_{t-1}\right)$$

然后利用reset gate计算新的记忆

$$\tilde{h}_{t} = \operatorname{tanh}(r_{t}\circ  Uh_{t-1} + Wx_{t} )$$

这里的意思是，之前的记忆由reset gate控制，如果reset gate元素都是0，则遗忘之前的事情。比如电影评论的情感分析，“有个文艺的少男爱死了一个平凡的少女，这个平凡的少女也爱死了那个文艺的少男，可两个人就是无法相会巴拉巴拉，真是个无聊的电影”。无论前面说了多少话，起决定性作用的可能就是“无聊”这个词。那么一些GRU可能会说，我遇到了一个情感强烈的词语，我不想让它被之前的记忆冲淡（求和），所以我把reset gate设为0，之前的记忆不起作用，把这个情感词汇写成新的记忆。

而update gate的作用是调节最后的更新，到底时刻$t$的记忆多少来自之前，多少来自当前：

$$h_{t} = (1 - z_{t}) \circ \tilde{h}_{t} + z_{t} \circ h_{t-1}$$

如果$z_t$是单位向量的话，则隐藏层只是复制前一个时刻的隐藏层，梯度不发生变化（衰减）。

这些公式写在一起已经非常直观了：

$$\begin{align*}
z_{t} &= \sigma(W^{(z)}x_{t} + U^{(z)}h_{t-1})&~\text{(Update gate)}\\
r_{t} &= \sigma(W^{(r)}x_{t} + U^{(r)}h_{t-1})&~\text{(Reset gate)}\\
\tilde{h}_{t} &= \operatorname{tanh}(r_{t}\circ  Uh_{t-1} + Wx_{t} )&~\text{(New memory)}\\
h_{t} &= (1 - z_{t}) \circ \tilde{h}_{t} + z_{t} \circ h_{t-1}&~\text{(Hidden state)}
\end{align*}$$

有些人觉得示意图更直观：

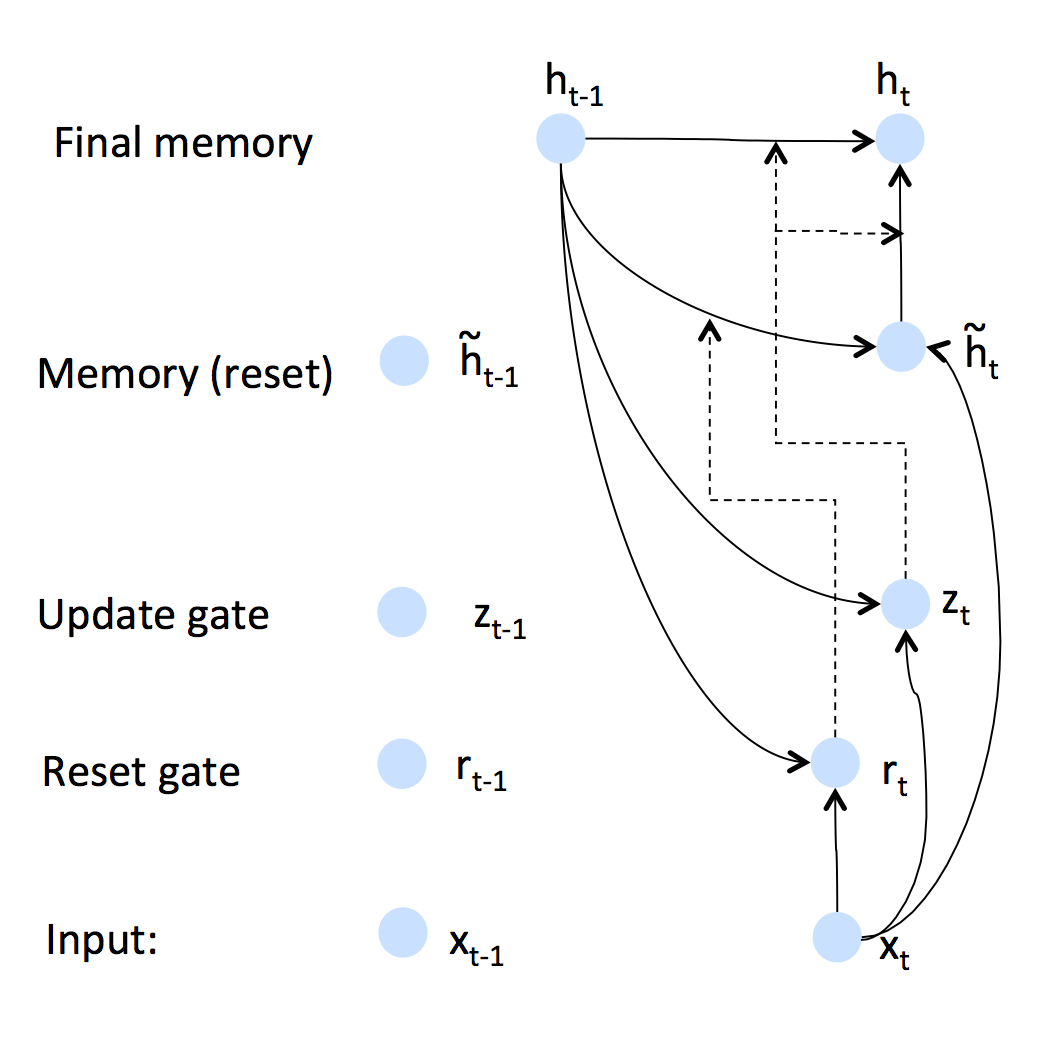
上图中，虚线代表某个gate的调节作用。隐藏层取决于上一个时刻的隐藏层和新的记忆，而update gate负责调节它们的比例，reset gate和输入共同决定新的记忆……

有人问这个reset gate是不是多余的，是不是可以直接让$h_{t} =  z_{t} \circ h_{t-1}$。做是的确可以这么做，但$x_t$永远无法把之前的记忆$h_{t-1}$“挤出去”，因为$z_t$是个求和的形式。

下面又是一张故弄玄虚的图：

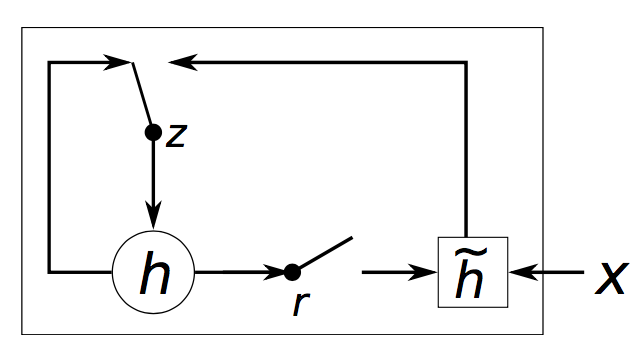
由于gate的调控作用是连续的而不是0或1，所以上图中的开关并不合理。

对于短距离的依存来讲，reset gate经常是激活的。

LSTM（Long-Short-Term-Memories）

LSTM与GRU动机相似，只不过单元结构有点不同。GRU的单元结构如下：

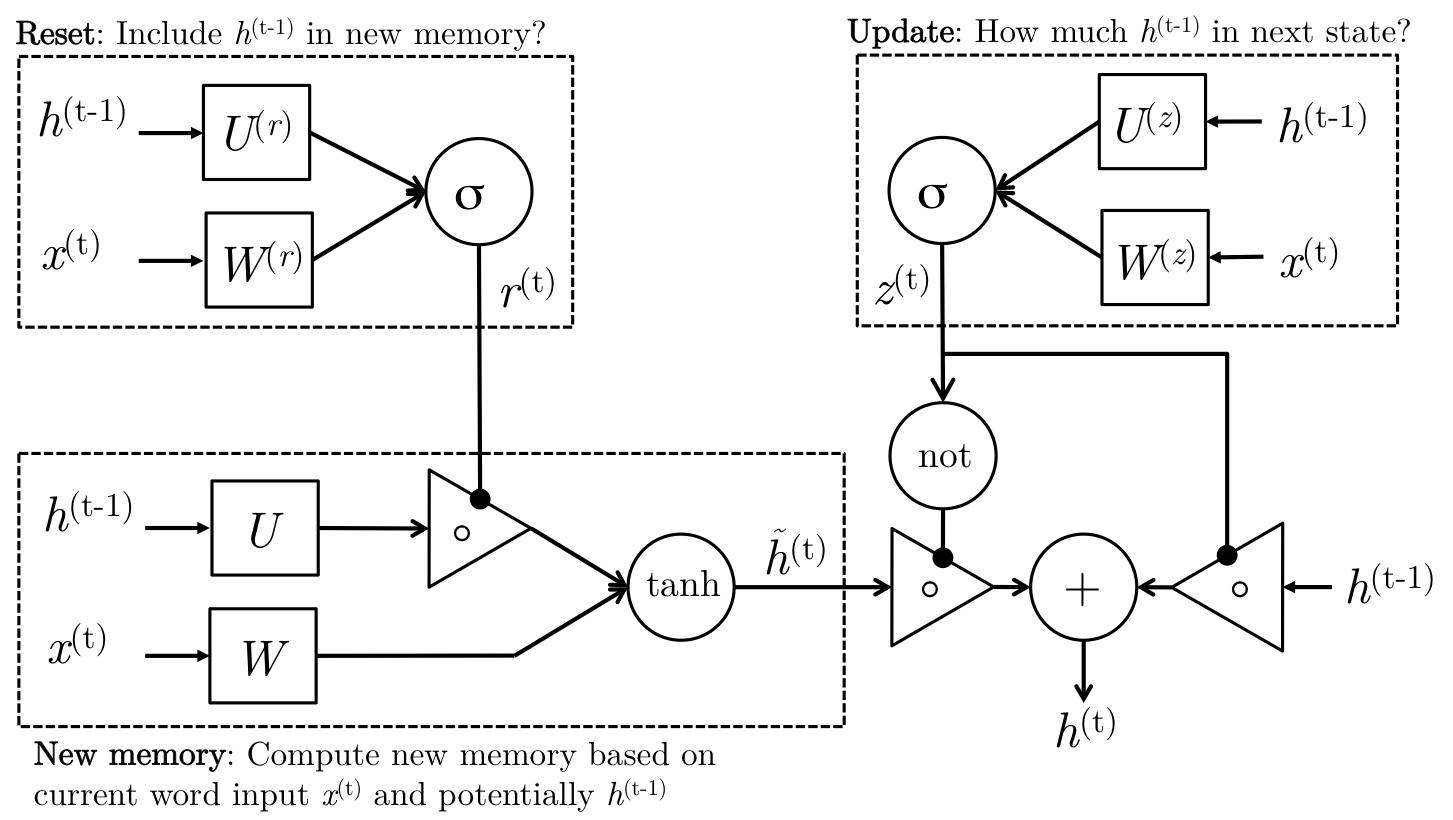
LSTM单元结构如下：

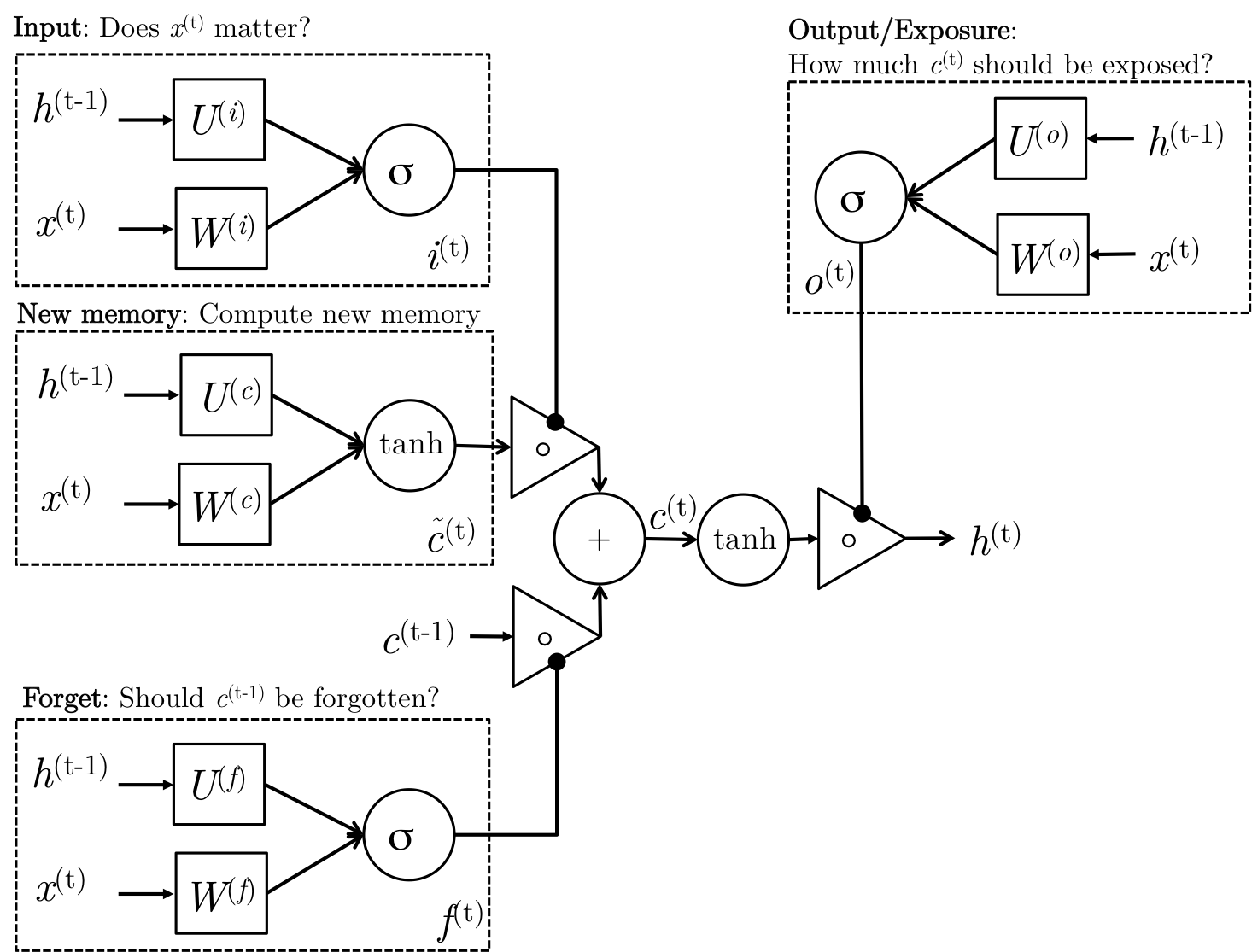
上图用公式描述如下：

$$\begin{align*}
i_{t} &= \sigma(W^{(i)}x_{t} + U^{(i)}h_{t-1})&~\text{(Input gate)}\\
f_{t} &= \sigma(W^{(f)}x_{t} + U^{(f)}h_{t-1})&~\text{(Forget gate)}\\
o_{t} &= \sigma(W^{(o)}x_{t} + U^{(o)}h_{t-1})&~\text{(Output/Exposure gate)}\\
\tilde{c}_{t} &= \operatorname{tanh}(W^{(c)}x_{t} + U^{(c)}h_{t-1})&~\text{(New memory cell)}\\
c_{t} &= f_{t} \circ c_{t-1} + i_{t} \circ \tilde{c}_{t}&~\text{(Final memory cell)}\\
h_{t} &= o_{t} \circ \operatorname{tanh}(c_{t})
\end{align*}$$

 LSTM的计算可以分为如下步骤

1.  New memory generation 与GRU的New memory generation类似。使用当前词语$x_t$ 和之前的隐状态$h_{t_1}$来生成新的记忆$\tilde{c}_{t}$。于是新记忆里面就包含了当前词语$x^{(t)}$的属性。

2. Input Gate 使用当前词语和之前的隐状态决定当前词语是否值得保留来gate新记忆，这个“是否”是通过$i_{t}$来体现的

3. Forget Gate 与input gate类似，只不过它不是用来衡量输入单词的有用与否，而是衡量过去的记忆对计算当前记忆有用与否。它接受输入单词和上一刻的隐状态产生输出 $f_{t}$。

4. Final memory generation 根据forget gate的建议$f_{t}$来遗忘过去的记忆$c_{t-1}$。类似地，根据input gate的建议$i_{t}$来gate信的记忆 $\tilde{c}_{t}$，然后把两者加起来得到最终记忆 $c_{t}$。

5. Output/Exposure Gate 这是GRU中不显式存在的门，用处是将最终记忆与隐状态分离开来。记忆 $c_{t}$ 中的信息不是全部都需要存放到隐状态中，隐状态是个很重要的使用很频繁的东西，LSTM中每个gate都需要隐状态的参与。Output Gate产生 $o_{t}$，用来gate记忆的tanh激活值。

一些可视化

一张最清晰的图示：

图源

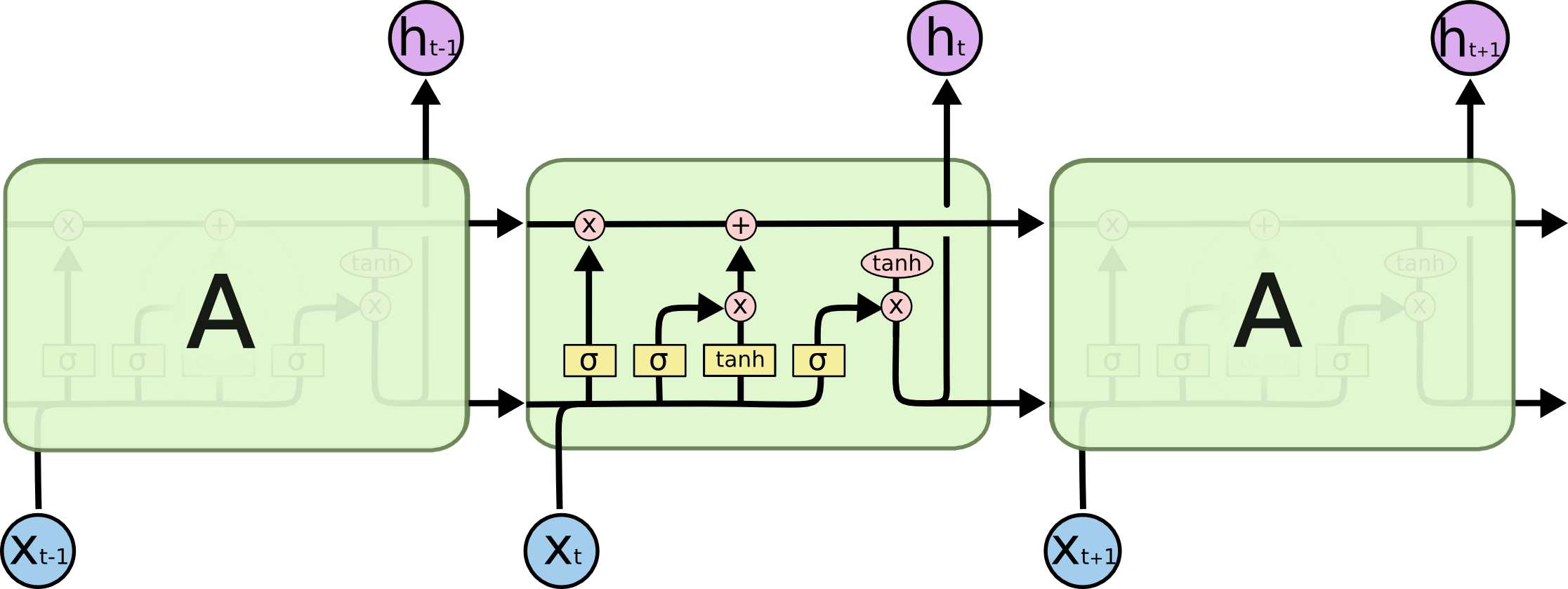
一些把简单问题复杂化的图示：

图源

图源

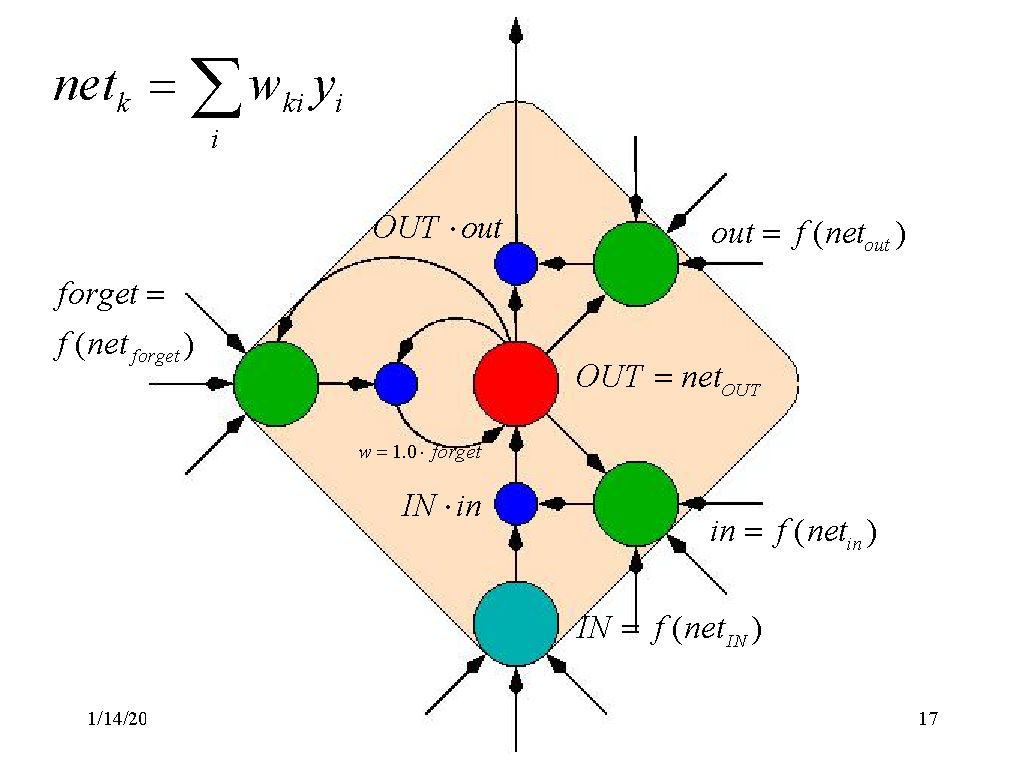
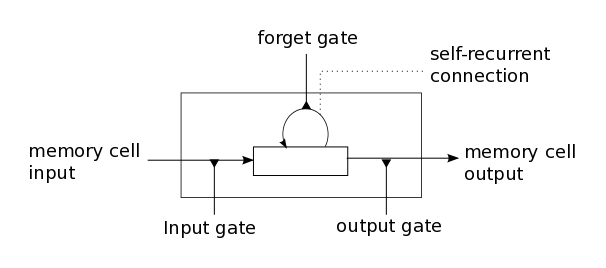
都没有公式一目了然

LSTM很潮

是序列标注、seq2seq任务的首选模型，可以层叠起来形成更深的模型。在数据量特别大的时候特别有用。

比如与传统MT模型的比较：

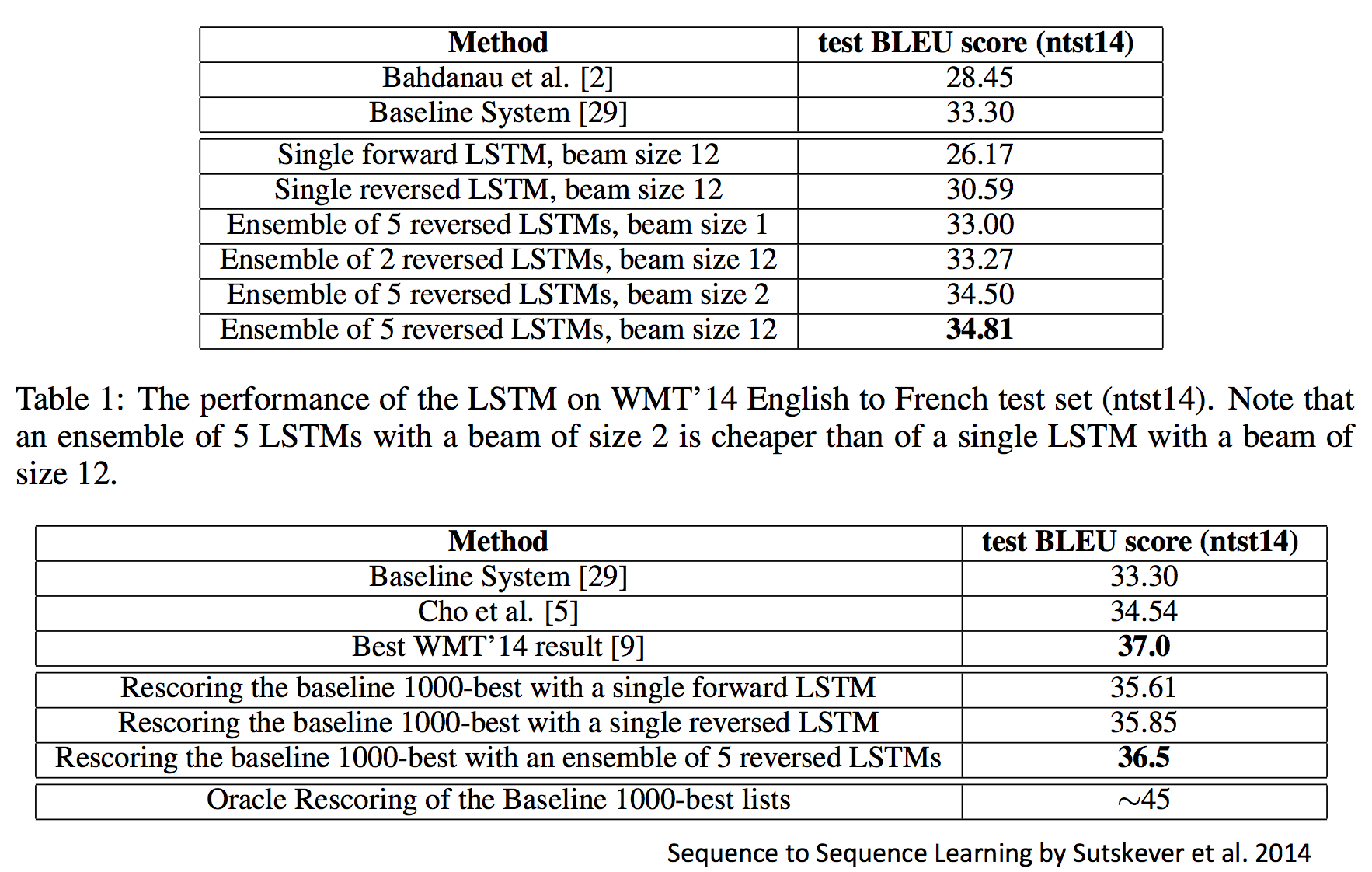
那时候的NN模型还是仅限于重新排序传统MT模型产生的结果，而最新的研究就是完全甩开了MT模型：

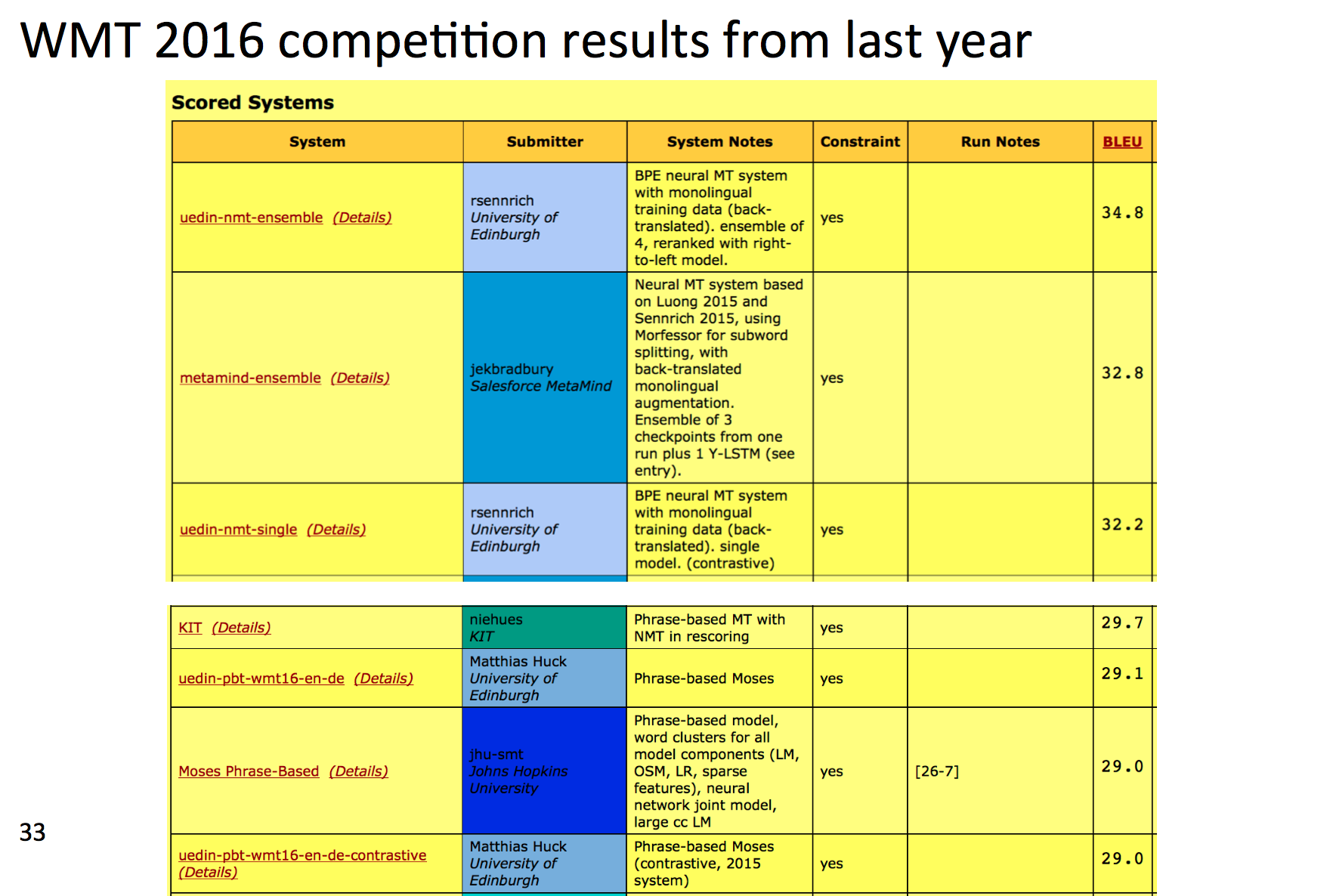
前三用的都是NN。

深度LSTM用于机器翻译

输入原文序列，将最后一个时刻的隐藏层向量PCA降维后可视化：

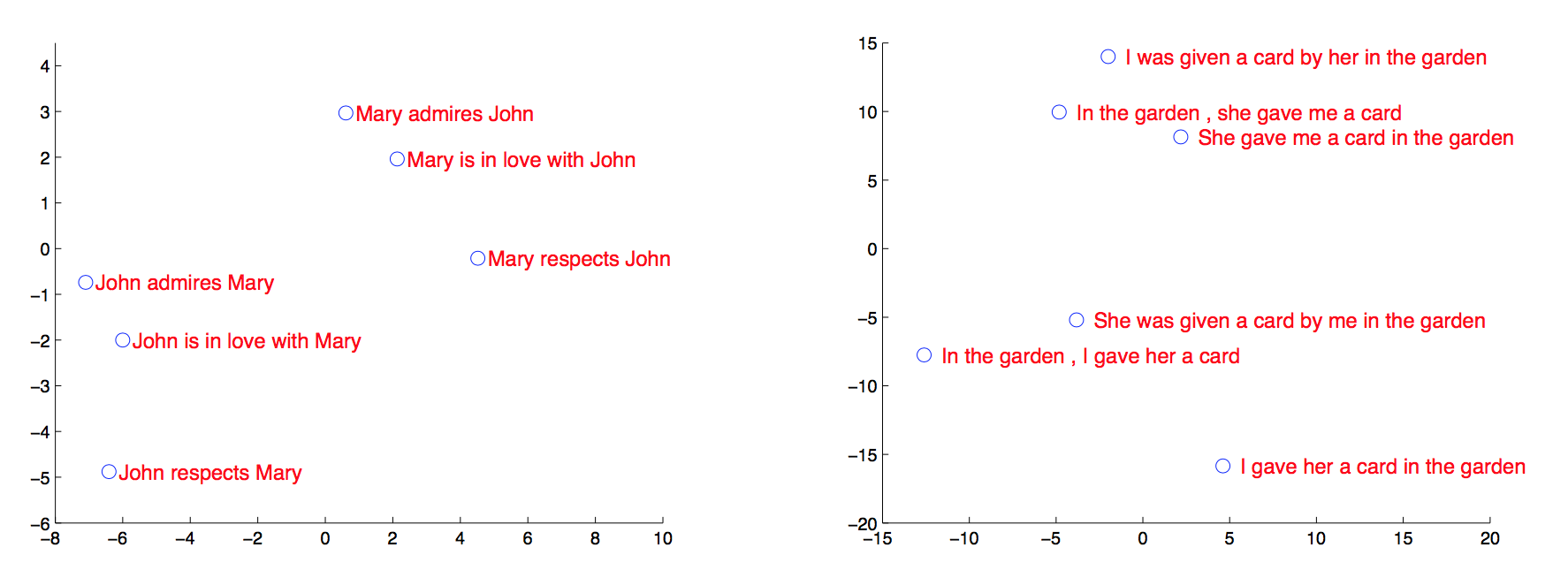
发现无论词序如何，意义相同的句子在向量空间中更接近。

进一步改进：更多门！

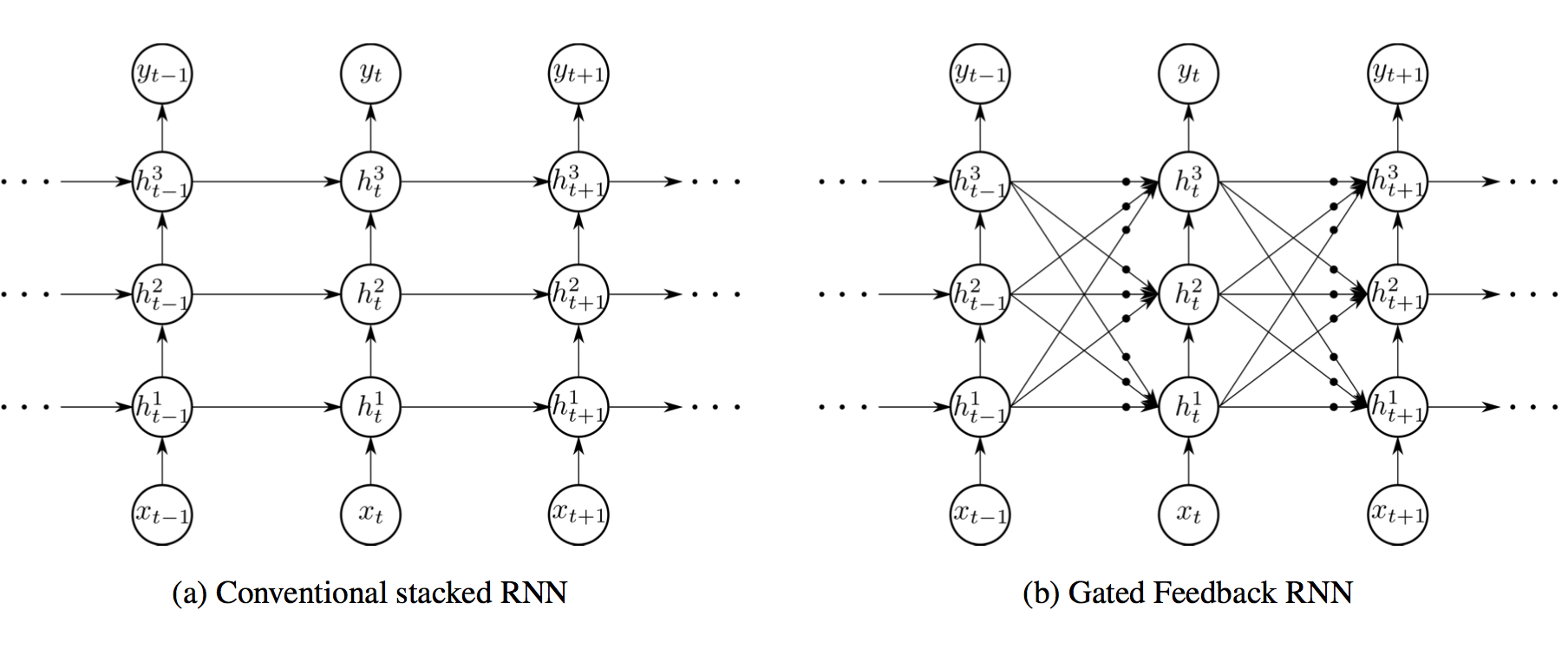
我感觉跟小孩玩乐高似的，拿着现有的单元拼拼凑凑成一个系统，跑出更高的分数就发paper了。至于为什么要这么拼这么改，不像理论完备的概率图模型，很少有人说得清楚吧。

RNN的最新改进

softmax的问题：无法出新词

对分类问题来讲，你无法指望分类模型给你分出一个训练集中不存在的类。即便是训练集中存在的类，如果样本数很少，模型也很难预测出该类。

对于预测下一个单词的语言模型来讲，也是如此。比如某某女士巴拉巴拉，然后自我介绍说我叫某某。如果某某不存在于训练集中，则模型无法预测出某某。

虽然可以用字符级的模型，但代价实在太大。

用指针来解决问题

如果把某某替换为“向前数第10个单词”这样的指针，问题就迎刃而解了。

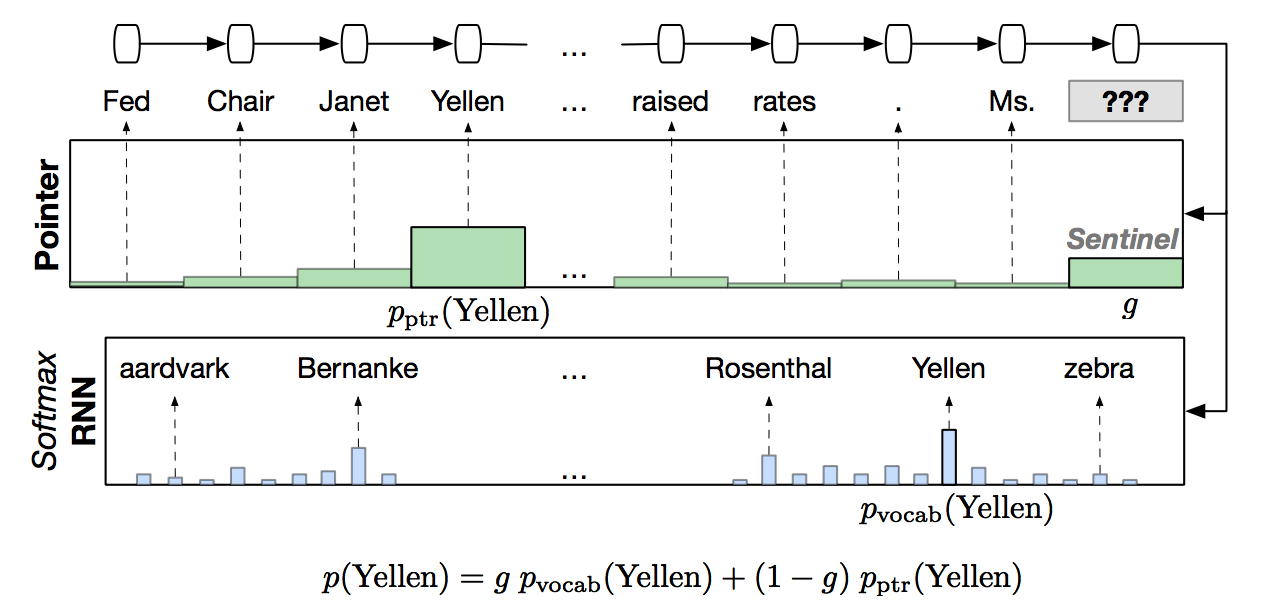
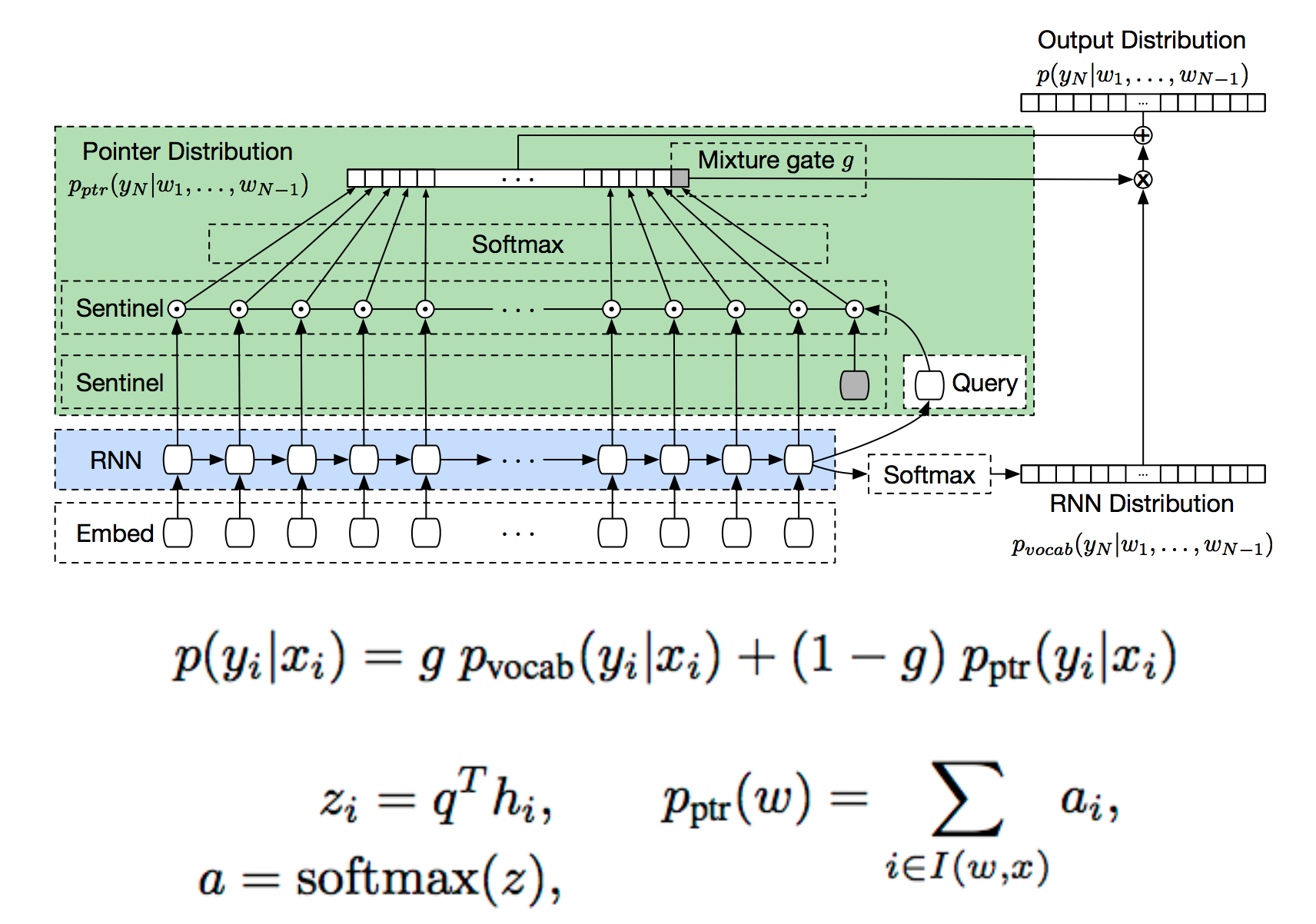
具体做法是，以前100个时刻的隐藏层作为输入，用一个softmax去计算前100个单词是pointer的概率，与原来的词表上的分布混合。

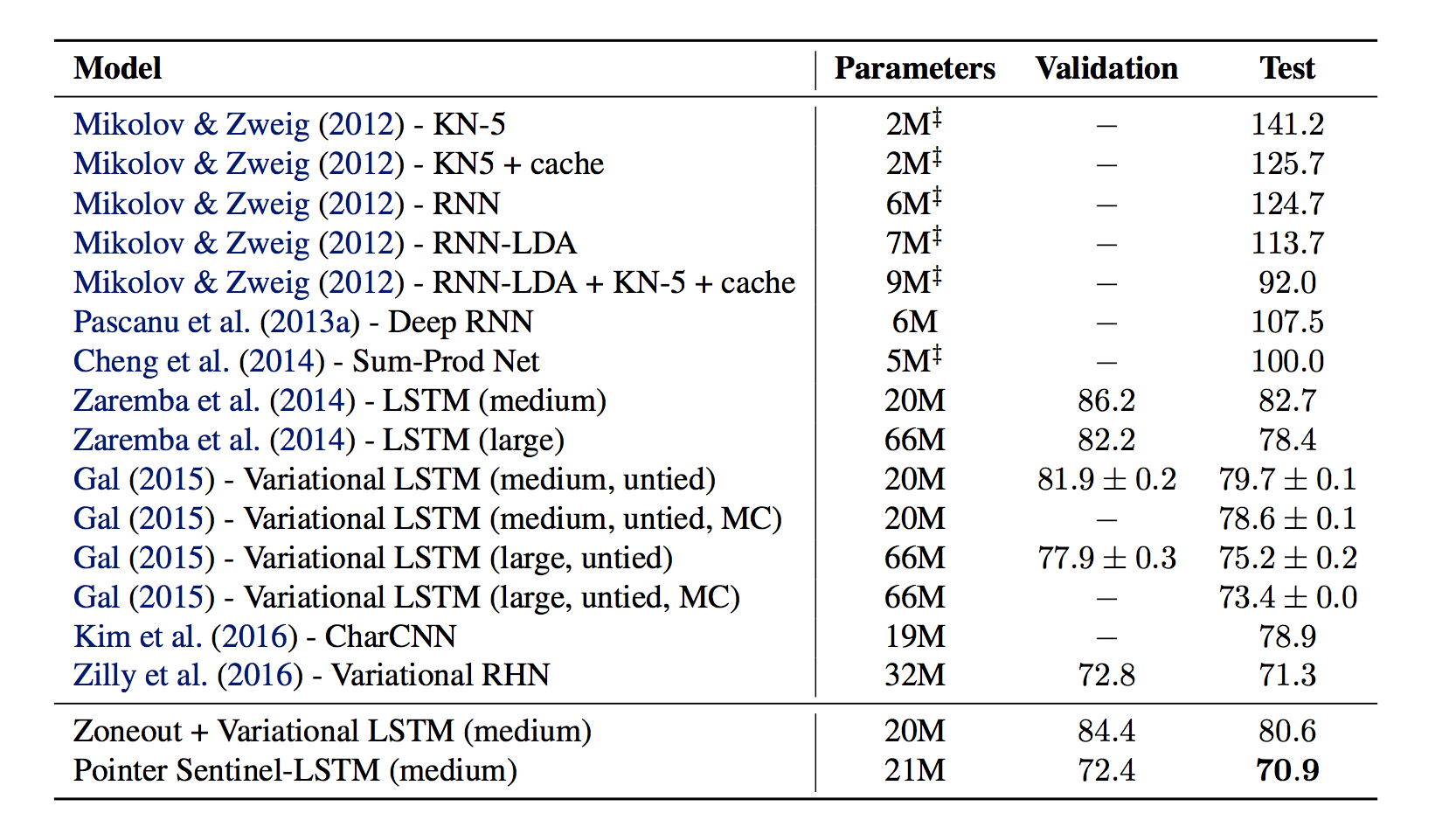
使用了pointer之后，困惑度下降了零点几个百分点：

总结

• RNN很强大

• 有很多进行中的工作

• GRU更强大

• LSTM又更强大

 知识共享署名-非商业性使用-相同方式共享：码农场 » CS224n笔记9 机器翻译和高级LSTM及GRU