目录
这节课介绍了根据上下文预测单词分类的问题,与常见神经网络课程套路不同,以间隔最大化为目标函数,推导了对权值矩阵和词向量的梯度;初步展示了与传统机器学习方法不一样的风格。
分类问题
给定训练集$$\{x^{(i)},y^{(i)}\}_1^N$$
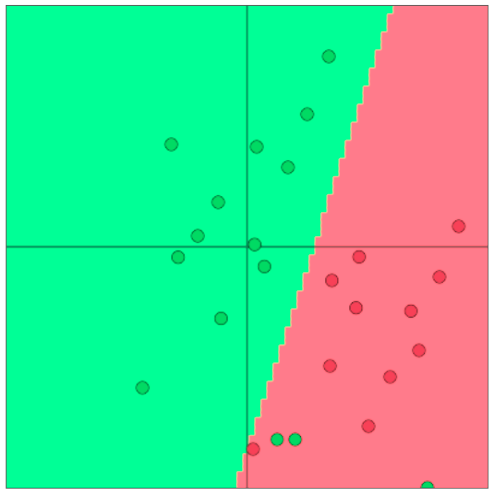
其中 $x^{(i)}$ 是一个 $d$-维向量,$y^{(i)}$ 是一个 $C$-维one-hot向量,$N$是总数。在传统的机器学习方法中,往往通过诸如逻辑斯谛回归和SVM找到分类决策边界:
softmax详细
softmax分类函数:
$$p(y_j = 1|x) = \frac{\exp(W_{j\cdot}x)}{\sum_{c=1}^C\exp(W_{c\cdot}x)}$$
计算方法分为两个步骤:取权值矩阵的某一行乘上输入向量,归一化得到概率。
softmax与交叉熵误差
训练的时候,可以直接最小化正确类别的概率的负对数:
$$-\log \bigg(\frac{\exp(W_{k\cdot}x)}{\sum_{c=1}^C\exp(W_{c\cdot}x)}\bigg)$$
其实这个损失函数等效于交叉熵:
$$\begin{align}H(\hat{y},y) &= -\sum_{j = 1}^{|V|} y_j \log(\hat{y}_j)\\
&=-\sum_{j=1}^{C}y_j\log(p(y_j = 1|x)) \\
&= -\sum_{j=1}^{C}y_j\log \bigg(\frac{\exp(W_{j\cdot}x)}{\sum_{c=1}^C\exp(W_{c\cdot}x)}\bigg)\\
&= -y_i \log(\hat{y}_i)\end{align}$$
这是因为类别是one-hot向量。
对N个数据点来讲有:
$$-\sum_{i = 1}^N\log \bigg(\frac{\exp(W_{k{(i)}\cdot}x^{(i)})}{\sum_{c=1}^C\exp(W_{c\cdot}x^{(i)})}\bigg)$$
加上正则化项有:
$$-\sum_{i = 1}^N\log \bigg(\frac{\exp(W_{k{(i)}\cdot}x^{(i)})}{\sum_{c=1}^C\exp(W_{c\cdot}x^{(i)})}\bigg) + \lambda \sum_{k=1}^{C\cdot d + |V|\cdot d} \theta_k^2$$
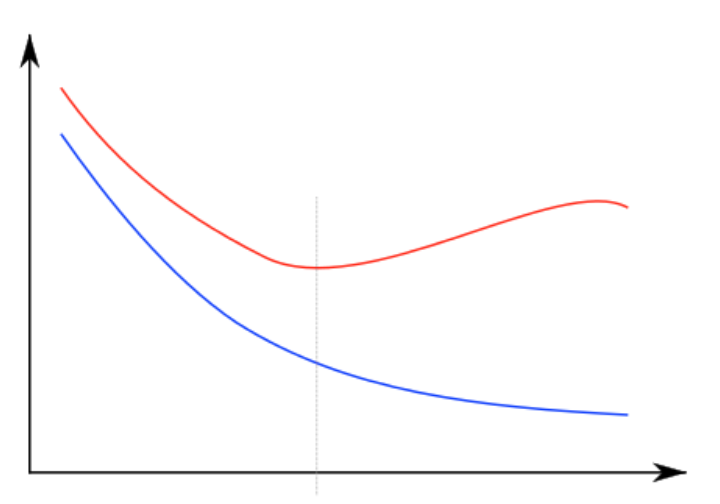
红线是test error,蓝线是training error,横轴是模型复杂度或迭代次数。直线是方差偏差均衡点。
优化
一般的ML问题中,参数由权值矩阵的列组成维度不会太大。而在词向量或其他深度学习中,需要同时学习权值矩阵和词向量。参数一多,就容易过拟合:
re-training词向量失去泛化效果
比如有一个给单词做情感分析的小任务,在预训练的词向量中,这三个表示电视的单词都是在一起的:
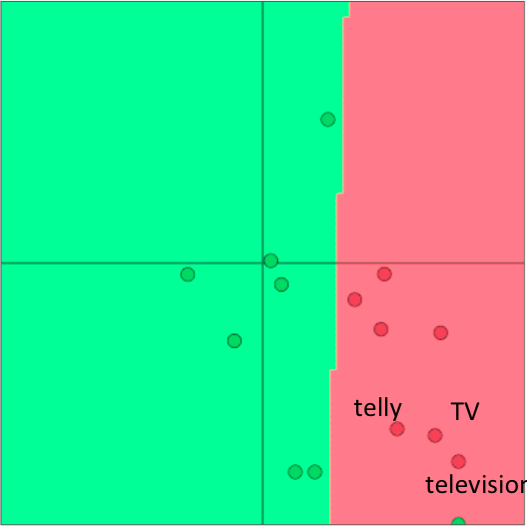
但由于情感分析语料中,训练集只含有TV和telly,导致re-training之后两者跑到别处去了:
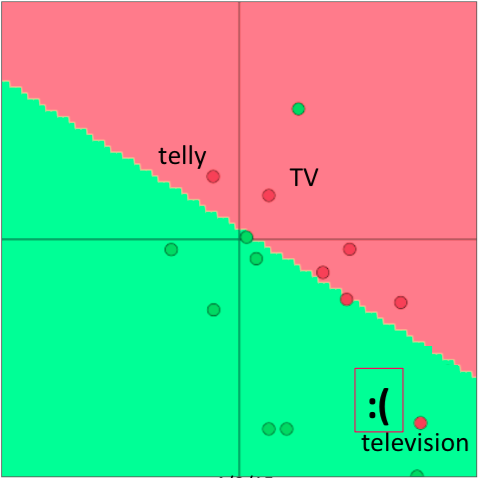
于是在测试集上导致television被误分类。
这个例子说明,如果任务的语料非常小,则不必在任务语料上重新训练词向量,否则会导致词向量过拟合。
顺便介绍一下词向量相关的术语:
词向量矩阵L常被称作lookup table:
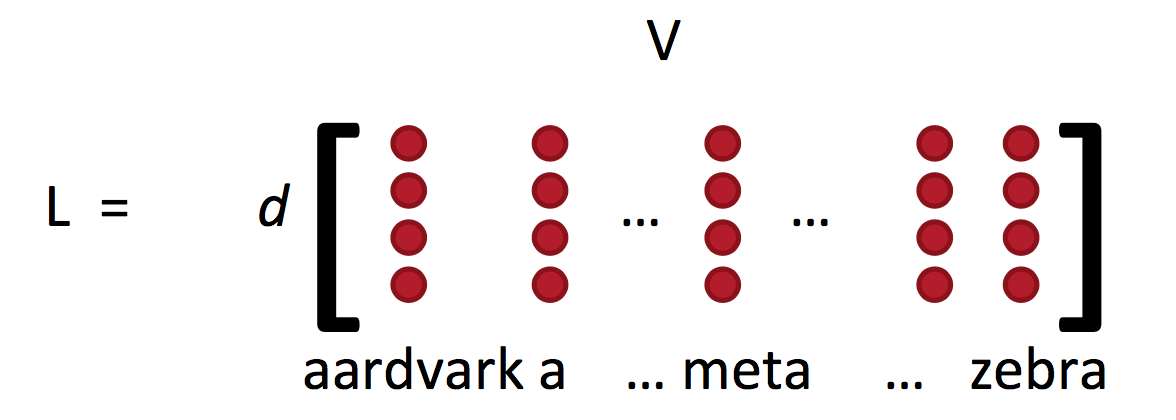
Word vectors = word embeddings = word representations (mostly)
可能有些人认为“词向量”是个很俗的翻译,但根据这门课的课件,其实与“词嵌入”是等价的。而且Rocher也几乎是一直在用word vector,而不是其他术语。
Window classification
这是一种根据上下文给单个单词分类的任务,可以用于消歧或命名实体分类。上下文Window的向量可以通过拼接所有窗口中的词向量得到:
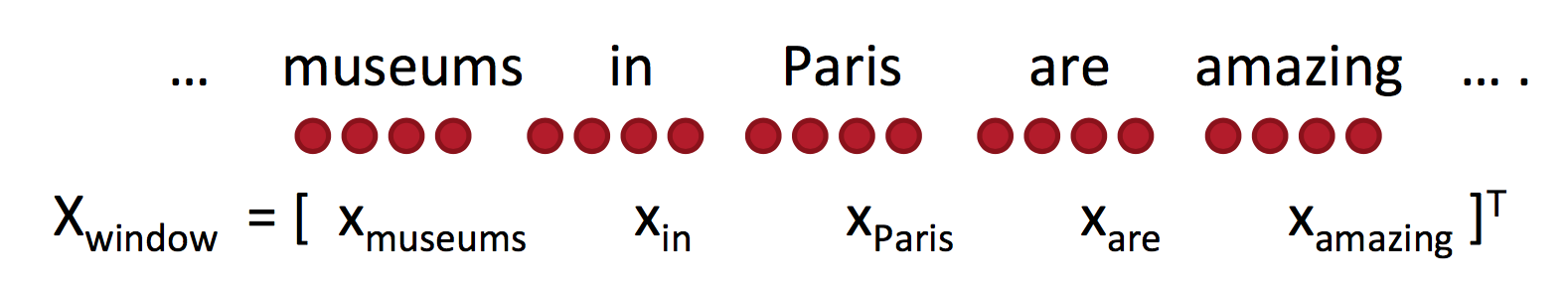
这是一个
![]()
的列向量。
最简单的分类器:softmax

$J$对$x$求导,注意这里的$x$指的是窗口所有单词的词向量拼接向量。
$$\begin{align}
\Delta_xJ &=\frac{\partial}{\partial x}-\log softmax\left(f_y(x)\right)\\
& = \sum_{c=1}^C-\frac{\partial \log softmax\left(f_y(x)\right)}{\partial f_c}\cdot \frac{\partial f_c(x)}{\partial x}\\
&=\left[
\begin{array}{c}
\hat{y_1}\\
\vdots\\
\hat{y}-1\\
\vdots\\
\hat{y_C}
\end{array}
\right]\cdot \frac{\partial f_c(x)}{\partial x}\\
&=\delta \cdot \frac{\partial f_c(x)}{\partial x}\\
&=\sum_{c=1}^C \delta_c W_c^T\\
&=W^T\delta \in \mathbb{R}^{5d}
\end{align}$$
于是就可以更新词向量了:
$$\nabla_{\theta} J(\theta) = \left[ \begin{array}{c} \nabla_{x_{museums}} \\ \vdots \\ \nabla_{x_{amazing}} \end{array} \right]$$
另一方面,对$W$求偏导数,将所有参数的偏导数写到一起有:
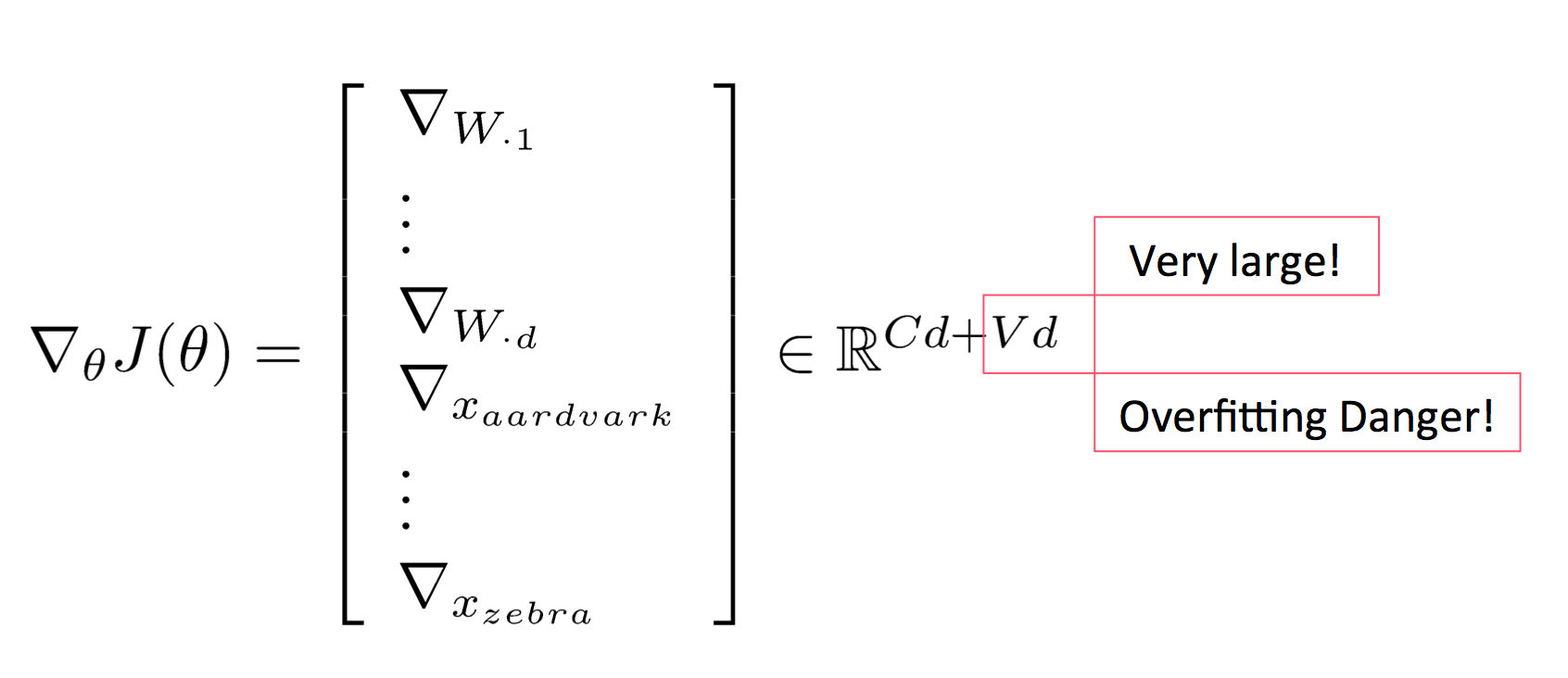
$$\nabla_{\theta} J(\theta) = \left[ \begin{array}{c} \nabla_{W_{\cdot 1}} \\ \vdots \\ \nabla_{W_{\cdot d}} \\ \nabla_{x_{aardvark}} \\ \vdots \\ \nabla_{x_{zebra}} \end{array} \right] \in \mathbb{R}^{Cd+Vd}$$
在更新过程中计算代价最高的有矩阵运算$f=Wx$和指数函数,但矩阵运算比循环要快多了(在CPU上快一个数量级)。
softmax(等价于逻辑斯谛回归)效果有限
仅限于较小的数据集,能够提供一个勉强的线性分类决策边界。
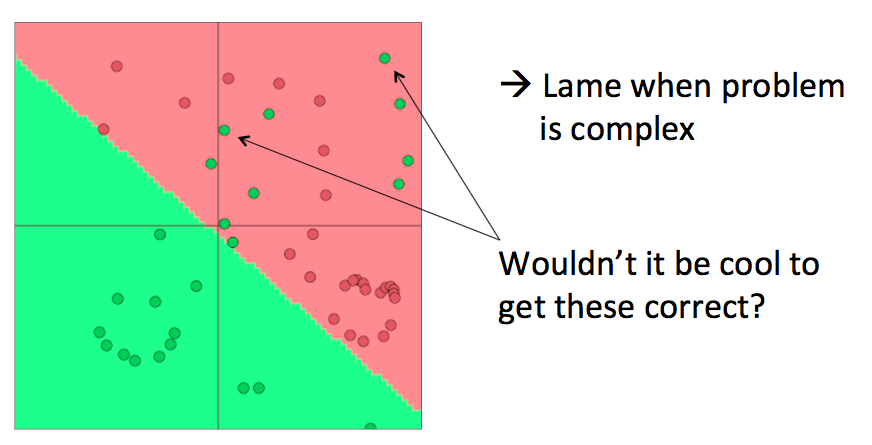
使用神经网络
神经网络可以提供非线性的决策边界:
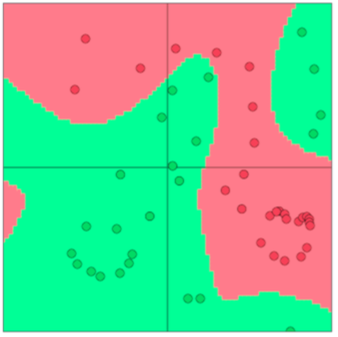
从逻辑斯谛回归到神经网络
老生常谈了,一些术语:
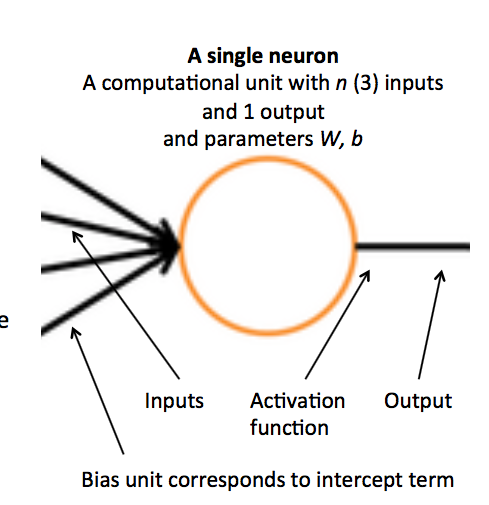
每个神经元是一个二分类逻辑斯谛回归单元:
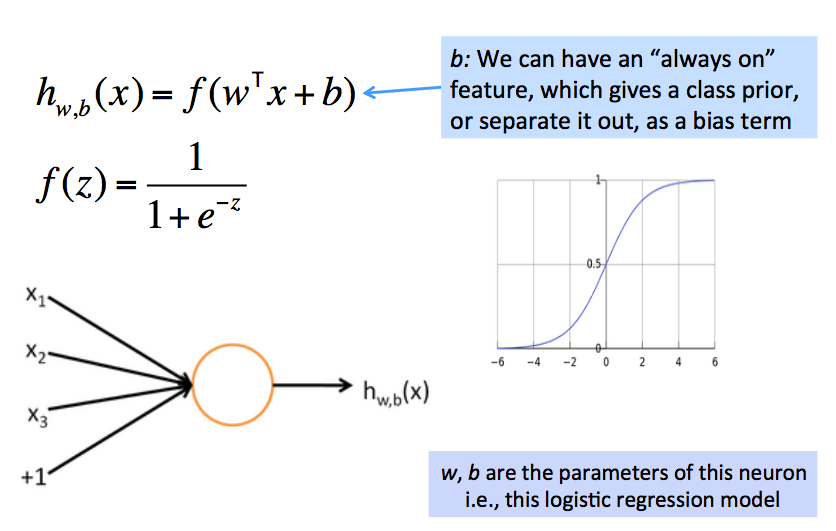
神经网络同时运行多个逻辑斯谛回归,但不需要提前指定它们具体预测什么:
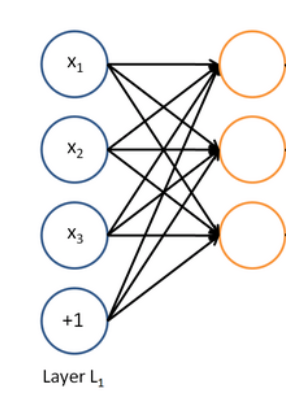
我们把预测结果喂给下一级逻辑斯谛回归单元,由损失函数自动决定它们预测什么:
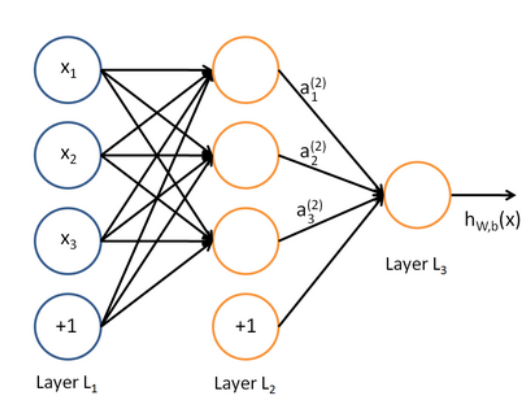
于是就得到了一个多层网络:
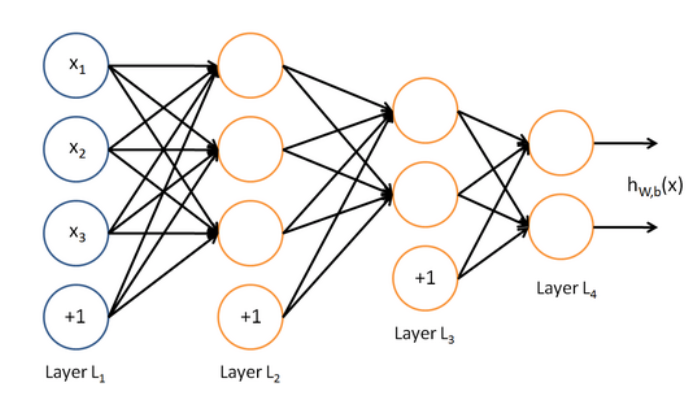
为什么需要非线性
因为线性系统所有层等效于一层:
$$W_1W_2x=Wx$$
而非线性模型可以捕捉很复杂的数据:
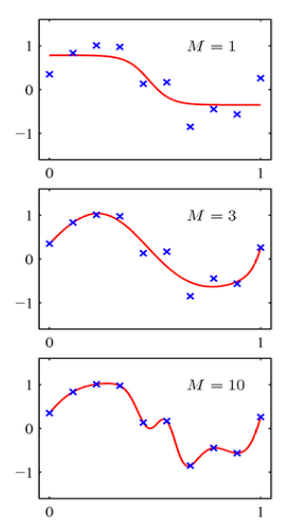
前向传播网络
一个简单的网络:
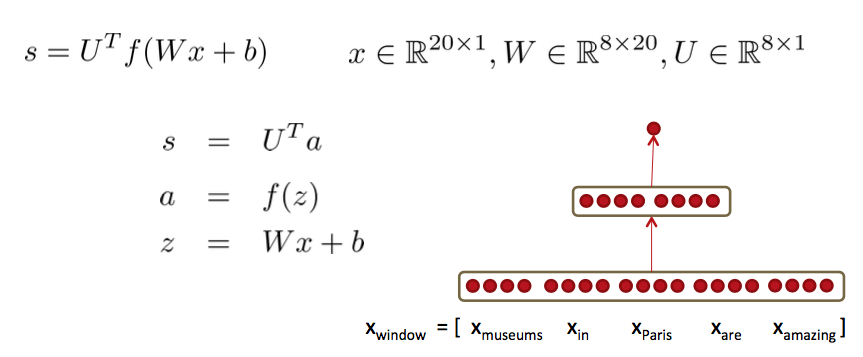
这种红点图经常在论文里看到,大致代表单元数;中间的空格分隔开一组神经元,比如隐藏层单元数为$2 \times 4$。$U$是隐藏层到class的权值矩阵:
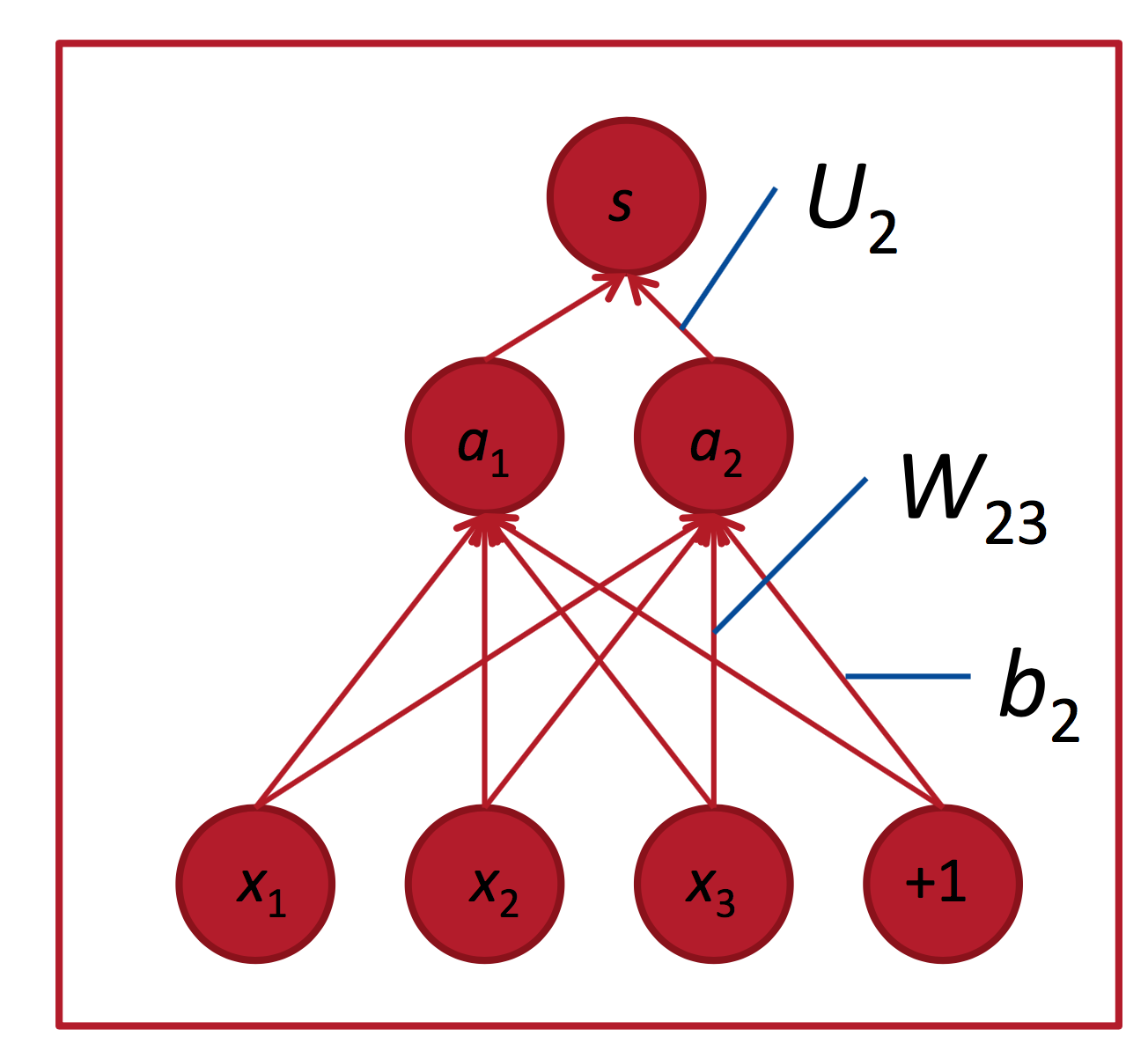
其中$a$是激活函数:
$$ a = \frac{1}{1 + \exp(-(w^Tx + b))}$$
或:
$$ a = \frac{1}{1 + \exp(-[w^T~~~b] \cdot[x~~~1])}$$
间隔最大化目标函数
怎么设计目标函数呢,记$s_c$代表误分类样本的得分,$s$表示正确分类样本的得分。则朴素的思路是最大化$(s - s_c)$ 或最小化 $(s_c - s)$。但有种方法只计算$s_c > s \Rightarrow (s_c - s) > 0$时的错误,也就是说我们只要求正确分类的得分高于错误分类的得分即可,并不要求错误分类的得分多么多么小。这得到间隔最大化目标函数:
$$minimize J = \max(s_c - s, 0)$$
但上述目标函数要求太低,风险太大了,没有留出足够的“缓冲区域”。可以指定该间隔的宽度$(s - s_c < \Delta)$ ,得到:
$$minimize J = \max(\Delta+s_c - s, 0)$$
可以调整其他参数使得该间隔为1:
$$minimize J = \max(1+s_c - s, 0)$$
这实际上是将函数间隔转换为几何间隔,参考SVM:http://www.hankcs.com/ml/support-vector-machine.html#h3-3
在这个分类问题中,这两个得分的计算方式为:$s_c = U^T f(Wx_c + b)$ 和 $s = U^T f(Wx + b)$;通常通过负采样算法得到负例。
另外,这个目标函数的好处是,随着训练的进行,可以忽略越来越多的实例,而只专注于那些难分类的实例。
反向传播训练
依然是老生常谈,跳过链式法则推导直接贴结果:
$$ \nabla_{W^{(k)}} = \begin{bmatrix} \delta_{1}^{(k+1)} a_1^{(k)} & \delta_{1}^{(k+1)} a_2^{(k)} & \cdots \\ \delta_{2}^{(k+1)} a_1^{(k)} & \delta_{2}^{(k+1)} a_2^{(k)} & \cdots \\ \vdots & \vdots & \ddots \end{bmatrix} = \delta^{(k+1)} a^{(k)T}$$
其中$\delta^{(k)}$是第$k$层的误差:
$$\delta^{(k)} = f'(z^{(k)}) \circ (W^{(k)T} \delta^{(k+1)}) $$
可见只要控制误差的计算方式,就可以smoothly地过渡到间隔最大化目标函数:
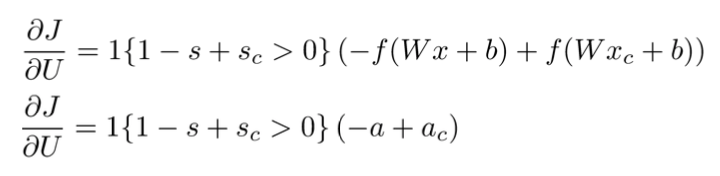
另外,对偏置的偏导数是$\delta^{(k)}_i$:
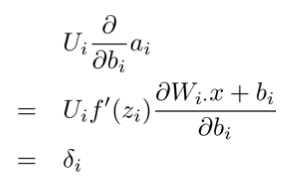
最后一片拼图是对词向量的偏导数,由于连接时每个输入单元连到了多个隐藏单元,所以对某个输入单元的偏导数是求和的形式(残差来自相连的隐藏单元):
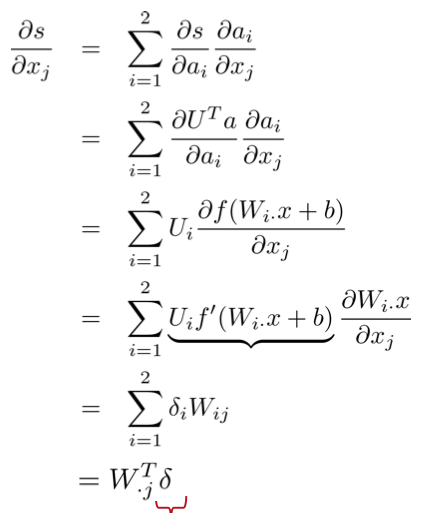
其中,$W_{\cdot j}^T$是第$j$列,转置后得到行向量;红色部分是误差,相乘后得到一个标量,代表词向量第$j$维的导数。那么对整个词向量的偏导数就是:
$$\frac{\partial s}{\partial x}=W^T\delta$$
 码农场
码农场