HMM与分词、词性标注、命名实体识别

HMM（隐马尔可夫模型）是用来描述隐含未知参数的统计模型，举一个经典的例子：一个东京的朋友每天根据天气{下雨，天晴}决定当天的活动{公园散步,购物,清理房间}中的一种，我每天只能在twitter上看到她发的推“啊，我前天公园散步、昨天购物、今天清理房间了！”，那么我可以根据她发的推特推断东京这三天的天气。在这个例子里，显状态是活动，隐状态是天气。

2014年11月23日更新：

我已利用HMM角色标注实现了中国人名、翻译人名、日本人名、地名、机构名等命名实体的识别，请参考此目录命名实体识别。

HMM描述

任何一个HMM都可以通过下列五元组来描述：

    :param obs:观测序列
    :param states:隐状态
    :param start_p:初始概率（隐状态）
    :param trans_p:转移概率（隐状态）
    :param emit_p: 发射概率 （隐状态表现为显状态的概率）

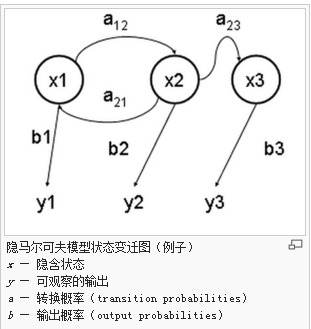
例子描述

这个例子可以用如下的HMM来描述：

states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {
    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
    }

emission_probability = {
    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

求解最可能的天气

求解最可能的隐状态序列是HMM的三个典型问题之一，通常用维特比算法解决。维特比算法就是求解HMM上的最短路径（-log(prob)，也即是最大概率）的算法。

稍微用中文讲讲思路，很明显，第一天天晴还是下雨可以算出来：

1. 定义V[时间][今天天气] = 概率，注意今天天气指的是，前几天的天气都确定下来了（概率最大）今天天气是X的概率，这里的概率就是一个累乘的概率了。

2.     因为第一天我的朋友去散步了，所以第一天下雨的概率V[第一天][下雨] = 初始概率[下雨] * 发射概率[下雨][散步] = 0.6 * 0.1 = 0.06，同理可得V[第一天][天晴] = 0.24 。从直觉上来看，因为第一天朋友出门了，她一般喜欢在天晴的时候散步，所以第一天天晴的概率比较大，数字与直觉统一了。

3. 从第二天开始，对于每种天气Y，都有前一天天气是X的概率 * X转移到Y的概率 * Y天气下朋友进行这天这种活动的概率。因为前一天天气X有两种可能，所以Y的概率有两个，选取其中较大一个作为V[第二天][天气Y]的概率，同时将今天的天气加入到结果序列中

4. 比较V[最后一天][下雨]和[最后一天][天晴]的概率，找出较大的哪一个对应的序列，就是最终结果。

这个例子的Python代码：

# -*- coding:utf-8 -*-
# Filename: viterbi.py
# Author：hankcs
# Date: 2014-05-13 下午8:51

states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {
    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
    }

emission_probability = {
    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

# 打印路径概率表
def print_dptable(V):
    print "    ",
    for i in range(len(V)): print "%7d" % i,
    print

    for y in V[0].keys():
        print "%.5s: " % y,
        for t in range(len(V)):
            print "%.7s" % ("%f" % V[t][y]),
        print


def viterbi(obs, states, start_p, trans_p, emit_p):
    """

    :param obs:观测序列
    :param states:隐状态
    :param start_p:初始概率（隐状态）
    :param trans_p:转移概率（隐状态）
    :param emit_p: 发射概率 （隐状态表现为显状态的概率）
    :return:
    """
    # 路径概率表 V[时间][隐状态] = 概率
    V = [{}]
    # 一个中间变量，代表当前状态是哪个隐状态
    path = {}

    # 初始化初始状态 (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]

    # 对 t > 0 跑一遍维特比算法
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}

        for y in states:
            # 概率 隐状态 =    前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率
            (prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            # 记录最大概率
            V[t][y] = prob
            # 记录路径
            newpath[y] = path[state] + [y]

        # 不需要保留旧路径
        path = newpath

    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])


def example():
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability)


print example()

输出：

           0       1       2
Rainy:  0.06000 0.03840 0.01344
Sunny:  0.24000 0.04320 0.00259
(0.01344, ['Sunny', 'Rainy', 'Rainy'])

NLP应用

具体到分词系统，可以将天气当成“标签”，活动当成“字或词”。那么，几个NLP的问题就可以转化为：

• 词性标注：给定一个词的序列（也就是句子），找出最可能的词性序列（标签是词性）。如ansj分词和ICTCLAS分词等。

• 分词：给定一个字的序列，找出最可能的标签序列（断句符号：[词尾]或[非词尾]构成的序列）。结巴分词目前就是利用BMES标签来分词的，B（开头）,M（中间),E(结尾),S(独立成词）

• 命名实体识别：给定一个词的序列，找出最可能的标签序列（内外符号：[内]表示词属于命名实体，[外]表示不属于）。如ICTCLAS实现的人名识别、翻译人名识别、地名识别都是用同一个Tagger实现的。

小结

HMM是一个通用的方法，可以解决贴标签的一系列问题。

 知识共享署名-非商业性使用-相同方式共享：码农场 » HMM与分词、词性标注、命名实体识别