A Hierarchical Bayesian Language Model based on Pitman-Yor Processes

这篇论文通过把unigram上的Pitman-Yor语言模型拓展到ngram，提出了一种新的平滑方法，同时在理论和试验上证明了有效性。

大部分概率语言模型都是$n$-gram模型，利用每个单词给定的$n-1$个上文单词预测该单词，并估计整个句子的概率：

$$\begin{equation}
P(sentence)\approx \prod^T_{i=1}P(word_i\vert word^{i-1}_{i-n+1})
\end{equation}$$

常用trigram，也即$n=3$。由于词表很大，即使这么小的$n$也会带来大量参数。一些平滑方法如interpolation或back-off只是在试验层面验证了有效性，没有回答“为什么有效”的问题。

这篇论文提出了一种用Pitman-Yor process做平滑的贝叶斯$n$-gram语言模型。

概率论复习

Multinomial Distribution

定义$K$为多项分布的类别数，每个样本可以表示为一个$K$维的独热向量，比如一个类别为$3$的样本可以表示为：

$$\mathbf{x}=(0,0,1,0,0,0)^\text{T}$$

记$x_k=1$的概率为参数$\mu_k$，则$\mathbf{x}$的分布为：

$$p(\mathbf{x}|\mathbf{\mu})=\prod_{k=1}^{K} \mu_{k}^{x_k}$$

其中$\mathbf{\mu}=(\mu_1,\cdots,\mu_K)^\text{T}$。这里的乘积形式不是代表这$k$个变量是独立的，而是一种数学上的美观。这些变量受到约束$\sum_{k=1}^Kx_k=1$，只有一个能等于$1$。同样，$\mu_k$也受到约束$\mu_k \ge 0, \sum_k\mu_k=1$。

整个数据集的似然函数是：

$$\begin{equation}
 p(\mathcal{D}|\mu ) = \prod\limits_{n = 1}^N {\prod\limits_{k = 1}^K {\mu _k^{{x_{nk}}}} }  = \prod\limits_{k = 1}^K {{\mu _k}^{(\sum\limits_n {{x_{nk}})} }}  = \prod\limits_{k = 1}^K {\mu _k^{{m_k}}}  \\
  \\
\end{equation}$$

给定$\mathbf{m}$和$N$，这样的数据集有$\left( \begin{gathered}
 N \\
 {m_1}{m_2} \cdots {m_k} \\
\end{gathered}  \right) = \frac{{N!}}{{{m_1}!{m_2}! \cdots {m_k}!}}$个，所以得到Multinomial Distribution的定义：

$${\text{Mult}}({m_1},{m_2}, \cdots ,{m_K}|\mu ,N) = \left( \begin{gathered}
 N \\
 {m_1}{m_2} \cdots {m_k} \\
\end{gathered}  \right)\mathop \prod \limits_{k = 1}^K \mu _k^{{m_k}}$$

Dirichlet Distribution

贝叶斯方法需要先选取参数（参数定义分布）的先验概率，然后乘以似然函数得到参数的后验概率。比如作为多项分布参数先验分布的Dirichlet分布：

$$\begin{equation}
\text{Dir}(\boldsymbol{\mu}\vert\boldsymbol{\alpha})=\frac{\Gamma(\alpha_{1}+\cdots+\alpha_{K})}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)}\prod_{k=1}^{K}\mu_{k}^{\alpha_{k}-1}
\label{eqn:dirichlet}
\end{equation}$$

这里的gamma函数定义如下：

$$\Gamma \left( x \right) = \int\limits_0^\infty  {{s^{x - 1}}{e^{ - s}}ds}  = x\Gamma (x - 1)$$

Dirichlet分布是Multinomial分布的共轭先验。首先将Dirichlet分布作为先验采样出多项式分布的参数$\mathbf{\mu}$，然后乘以似然函数得到参数的后验概率：

$$p(\mu |{\cal D},\alpha ) \propto {\color{red} p({\cal D}|\mu )} {\color{blue} p(\mu |\alpha )} \propto \prod\limits_{k = 1}^K {\mu _k^{{\alpha _k} + {m_k} - 1}}$$

其中$\mathbf{\mu}$是多项式分布的参数，$\mathcal{D}$是数据集，$\mathbf{\alpha}$是Dirichlet分布的参数。蓝色是先验，红色是似然函数。我们发现上式后验概率的形式与Dirichlet相同，这说明Dirichlet分布的确是Multinomial分布的共轭先验。

观察上式与式（3），得到归一化系数，于是贝叶斯方法下的后验分布为：

$$\begin{equation} \begin{aligned}
 p(\mu |D,\alpha ) &= {\text{Dir}}(\mu |\alpha  + {\mathbf{m}})  \\
  &= \frac{{\Gamma ({\alpha _1} +  \cdots  + {\alpha _K} + N)}}{{\Gamma ({\alpha _1} + {m_1}) \cdots \Gamma ({\alpha _K} + {m_K})}}\prod\limits_{k = 1}^K {\mu _k^{{\alpha _k} + {m_k} - 1}}   \\
\end{aligned} \end{equation} $$

其中$\mathbf{m}=(m_1,\cdots,m_K)^\text{T}$，为试验观测到的数据。Dirichlet先验的参数$\alpha_k$则可以解读为对观测到$x_k=1$的次数的先验知识。

Dirichlet Process

实际上很难知道（或不可能知道）数据到底来自几个分布。假设来自$K$个，$K$越大，模型复杂度越大。当模型比数据量复杂的时候，就过拟合了；当模型比数据简单的时候，就欠拟合了。靠人拍脑袋决定模型复杂度是很困难的，有没有办法根据数据量自动确定模型复杂度呢？

考虑一个由$K$个components组成的Bayesian mixture model:

$$\begin{equation} \begin{aligned}
 \pi |\alpha  &\sim {\text{Dir}}(\frac{\alpha }{K}, \cdots ,\frac{\alpha }{K}) \hfill  \\
 {z_i}|\pi  &\sim {\text{Mult}}(\pi ) \hfill  \\
\end{aligned} \end{equation} $$

也即从Dirichlet分布采样mixing proportions $\pi$，然后根据$\pi$决定数据来自哪个component $z_i$，最后根据$z_i$采样出数据$x_i$（如果对所有的$z$上$x$的条件概率求和，则称为marginalizing out）。

这相对于一般的mixture model而言，额外多了个parametrized Dirichlet prior over mixing proportion的过程，于是有结论：当component数量$K$很大的时候，给定$n$个样本，它们实际上来自的component个数并不是$K$，而是$O(\alpha\log n)$。如果$K \to \infty$，则称这样的模型为 infinite mixing model。由于component数量只与数据量有关，所以这样的模型能够自动根据数据量调整复杂度。

给定一个定义在$\Theta$上的base distribution $H$和一个正实数的concentration parameter $\alpha$，Dirichlet Process是用来采样随机分布$G$的过程，记作 $G\sim{\text{DP}}(\alpha H)$。对空间$\Theta$的任何partition $A_r,\cdots,A_r$，向量$(G({A_1}), \cdots ,G({A_r}))$也是随机的，需满足：

$$\begin{equation} \begin{aligned}
 (G({A_1}), \cdots ,G({A_r}))\sim{\text{Dir}}(\alpha H({A_1}), \cdots ,\alpha H({A_r})) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

上式其实在说，$G$的边缘分布必须是Dirichlet distributed。只有满足了这些条件，Dirichlet Process才成立。DP的参数具有如下性质：

对任意$A \subset \Theta$，有

$$\begin{equation} \begin{aligned}
 E[G(A)] &= H(A) \hfill  \\
 V[G(A)] &= \frac{{H(A)(1 - H(A)}}{{\alpha  + 1}} \hfill  \\
\end{aligned} \end{equation} $$

其中，$\alpha$又称concentration参数，越大的话DP将越多的概率质量集中在均值附近。如果$\alpha \to \infty$，则$G(A) \to H(A)$。

然而DP只是个理论上的随机过程，infinite dimension（空间划分的集合数）是无法计算的。这时候就需要有一种可计算的算法，在下一章描述。

中餐馆过程

DP有一个性质叫做clustering property。假设有$n \in \mathbb{N}$个自然数，将其划分为任意个子集，称这样的一次划分为一个“划分（partition）”。我们想要得到定义在划分上的分布，即某个划分出现的概率。由于所有划分的数量没有closed form，只知道它的上限是$O(n^n)$，所以无法直接用组合数学去计算。

某个中餐馆有无限多个桌子，顾客进门后按如下随机过程入座：

1.第一个顾客总是选择第一个桌子

2.第$n$个顾客以$\frac{\alpha}{n-1+\alpha}$的概率选择第一个空桌子，以$\frac{c}{n-1+\alpha}$选择某个非空的桌子；其中$\alpha$为随机过程的一个参数，$c$为该桌子已经入座的人数。

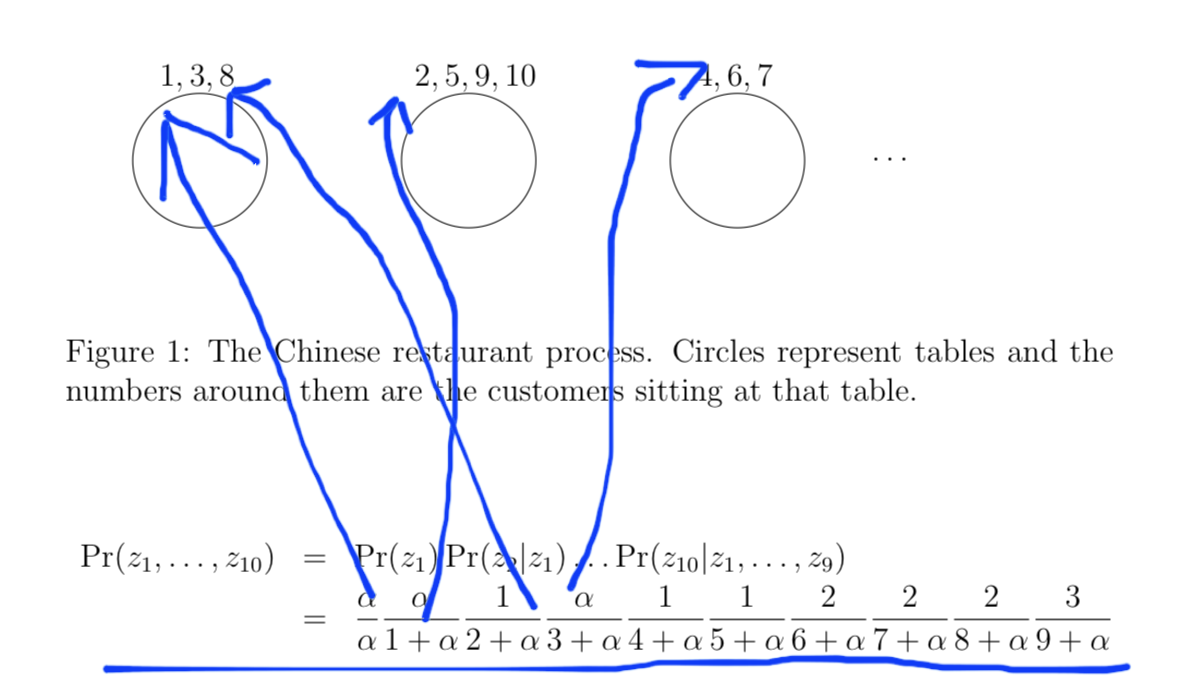
这个随机过程实际上定义了一个概率分布，记第$n$个顾客入座后非空的桌子数为$k_n$，其中$1\le k_n \le n$；这$k_n$张桌子的人数的状态就由上述过程定义了。比如一个$10$人入座的状态的概率计算如下：

COS 597C: Bayesian nonparametrics

事实上，顾客的排列组合不影响入座状态的概率，因为顾客排列组合只导致上式的分子跟着排列组合，不影响分母（另外，该过程得名的原因也是由于中餐馆的桌子是圆形的，同一张桌子上的顾客不存在“位置”）。同时，桌子人数的排列组合也不影响结果。也就是说所有$3+3+4$的入座状态（包括$3+4+3$、$4+3+3$）的概率都是上面这个表达式。

一般化表述，

$$\begin{array}{l}
P({\pi _{[N]}}) &= \frac{1}{{\alpha (\alpha  + 1) \cdots (\alpha  + N - 1)}}\prod\limits_{c \in {\pi _{[N]}}} {\alpha (|c| - 1)!}  \\
& = \frac{{{\alpha ^K}}}{{\alpha (\alpha  + 1) \cdots (\alpha  + N - 1)}}\prod\limits_{c \in {\pi _{[N]}}} {(|c| - 1)!}
\end{array}$$

可见起作用的只有每个cluster（table）的$c$，而与顾客的label或table的label无关（注：由于新桌子采样自$G_0$，所以可能与旧桌子是同一个label）。

将table当作类别，每个顾客当作一次采样，CRP实际上实现了infinite dimension的dirichlet process。

将table当作单词（或说每个table都上一种dish），顾客们当作一个单词序列，中餐馆过程实际上描述了一种unigram模型。然而，该分布不符合自然语言规律的一点是，它并不是power law distribution：

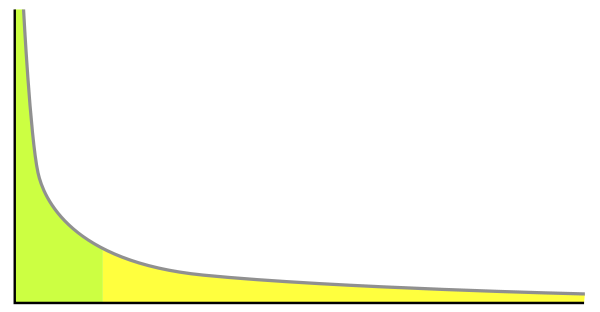
（$y=ax^{-k}$大部分区域的概率密度或质量很小，图片来源wiki）

下一章介绍克服了这一点的一种extension。

Pitman-Yor Process

Pitman-Yor Process是nonparametric Bayesian models（贝叶斯学派利用数据决定模型复杂度的方法）的一种，此处用于建模unigram语言模型。定义$W$为词表，含有有限的$V$个单词。每个单词$w \in W$出现的概率为$G(w)$，所有单词的概率形成向量$G=[G(w)]_{w \in W}$。假设$G$的先验是Pitman-Yor Process：

$$\begin{equation}
G \sim \text{PY}(d,\theta,G_0)
\end{equation}$$

其中，参数$0 \le d < 1$，$\theta > -d$，$G_0=[G_0(w)]_{w \in W}$，$G_0(w)$是单词$w$的先验概率(未观测任何数据之前的假设)，一般取均匀分布$G_0(w)=\frac{1}{V}$。$d$和$\theta$都是控制在$G_0$附近变化的参数，$d$叫做discount参数，待会儿会在采样过程中看到为什么叫这个名字。如果$d=0$，那么Pitman-Yor过程就退化为Dirichlet过程$DP(\theta,G_0)$。$\theta$叫concentration参数，当$\theta \to \infty$，$G \to G_0$。

当词表有限时，$PY(d,\theta,G_0)$没有closed form，但不妨碍用来做语言模型。假设单词序列$x_1,x_2,\cdots$是独立同分布地从$G$中取样产生的，那么Pitman-Yor过程就是将$G$ marginalize out的一个生成过程。这可以通过将$x_i$关联到由$PY$过程的参数$G_0$取样得到的$y_i$来实现：

第一个单词$x_1$一定与从$G_0$取样的$y_1$相同。设$t$为当前已经从$G_0$取样的单词数（此时$t=1$），$c_k$为事件$x_k=y_k$的次数（此时$c_1=1$），于是$c_.=\sum_{k=1}^tc_k$为从$G$取样的所有样本数。

之后的每个单词$x_{c_.+1}$，要么以$\frac{c_k-d}{\theta+c_.}$的概率重复某一次采样到的$y_k$（递增$c_k$；赋值$x_{c_.+1} \leftarrow y_k$）；要么以$\frac{\theta+dt}{\theta+c_.}$从$G_0$重新取样（递增$t$；赋值$c_t=1$；采样$y_t \sim G_0$；赋值$x_{c_.+1} \leftarrow y_t$）。

第一个分支其实拥有$t$个子分支，由于$c_.=\sum_{k=1}^tc_k$，所以$\sum_{k=1}^t \frac{c_k-d}{\theta+c_.}+\frac{\theta+dt}{\theta+c_.}=1$，两个主分支形成了一个概率分布。

上述过程独立同分布地从$G$采样得到了一个单词序列，却没有显式地采样，而是把$G$ marginalize out。这个过程有几个性质：

1、rich-gets-richer clustering property：一个词重复得频繁，会导致它重复得更频繁（$\frac{c_k-d}{\theta+c_.}$）。

2、从$G_0$采样越频繁，会导致从$G_0$采样越频繁（$\frac{\theta+dt}{\theta+c_.}$）。

这两点导致该过程产生的unigram模型比较符合自然语言的规律：有大量词汇，大部分都是稀有词。当$d>0$时，该过程产生的长$T$的文本中的词汇量是$O(\theta T^d)$。当$\theta=0$时，这就是Dirichlet分布，词汇量增长速度变慢，为$O(\theta \log T)$。

Hierarchical Pitman-Yor语言模型

无限大词表的unigram语言模型，非常吸引人。如何拓展到ngram呢？ngram模型中当前词语出现的概率由前$n-1$个单词（上文${\mathbf{u}}$）决定，记作$G_\mathbf{u}(w)$。

我们认为这些概率分布$G_\mathbf{u}[G_\mathbf{u}(w)]_{w \in W}$的先验是Pitman-Yor process：

$$\begin{equation} \begin{aligned}
 {G_{\mathbf{u}}}\sim{\text{PY}}({d_{|{\mathbf{u}}|}},{\theta _{|{\mathbf{u}}|}},{G_{\pi ({\mathbf{u}})}}) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

其中，${\pi ({\mathbf{u}})}$是$\mathbf{u}$去掉第一个单词之外的后缀。$d$和$\theta$都是关于上文${|{\mathbf{u}}|}$的长度的函数。Mean vector ${G_{\pi ({\mathbf{u}})}}$是给定上文除去最初单词时当前单词出现的概率。由于我们不知道${G_{\pi ({\mathbf{u}})}}$，所以我们递归地利用上式作为${G_{\pi ({\mathbf{u}})}}$的先验，但这次使用参数${d_{|\pi ({\mathbf{u}})|}},{\theta _{|\pi ({\mathbf{u}})|}},{G_{\pi (\pi ({\mathbf{u}}))}}$。这个过程一直递归到空白上文$\emptyset$为止。此时，我们给${G_\emptyset }$一个Pitman-Yor先验：

$$\begin{equation} \begin{aligned}
 {G_\emptyset }\sim{\text{PY}}({d_0},{\theta _0},{G_0}) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

其中，$G_0$是全局mean vector，每个$G_0(w)=\frac{1}{V}$；$d_0$的先验是均匀分布，而$\theta_0$的分布是$\text{Gamma}(1,1)$。

这种先验的结构其实是一颗后缀树，但越靠近根部的节点反而是越后面的单词，每个孩子都在父节点的上文之前增加一个单词。这种结构的用意在于，越早出现的单词对当前单词的影响越弱。所以从叶节点到根节点的过程中，它们被第一个丢掉。

比如生成如下句子

the lazy dog
the lazy cat
the lazy cat
that lazy fox
that lazy fox
that lazy fox

的过程：

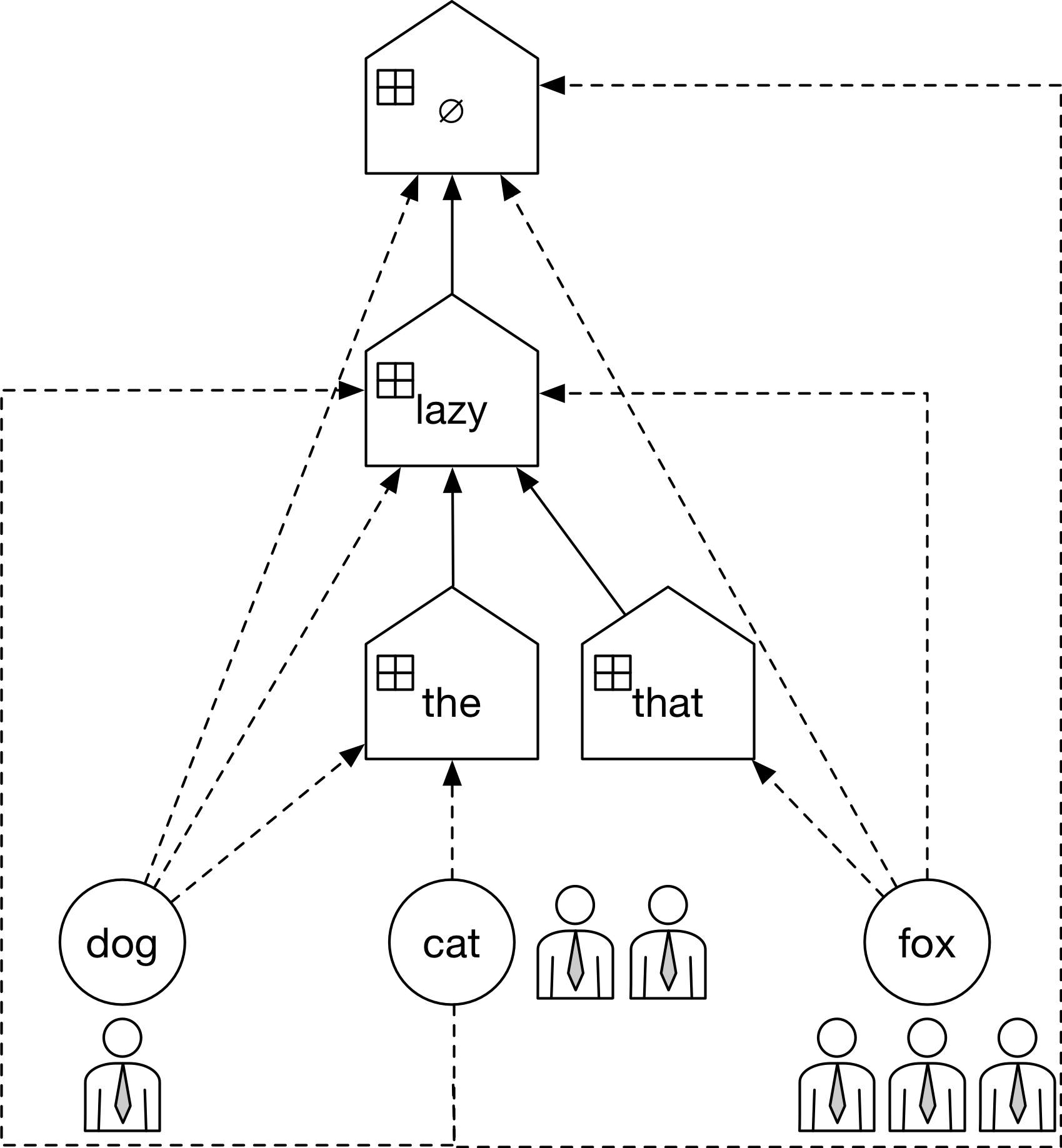
实线表示$\mathbf{u}$构成的trie树，房形表示餐馆，小圆圈表示桌子，虚线表示桌子$w$隶属于该餐馆，顾客表示一次计数。

此时估计“the lazy fox”的概率：

$$\begin{equation} \begin{aligned}
 {G_{{\text{the lazy}}}}({\text{fox}})&\sim{\text{PY}}({d_2},{\theta _2},{G_{{\text{lazy}}}}({\text{fox}})) \hfill  \\
&  \sim{\text{PY}}({d_2},{\theta _2},{\text{PY}}({d_1},{\theta _1},{G_\emptyset }({\text{fox}}))) \hfill  \\
 &\sim{\text{PY}}({d_2},{\theta _2},PY({d_1},{\theta _1},{\text{PY}}({d_0},{\theta _0},{G_0}))) \hfill  \\
\end{aligned} \end{equation} $$

注：这不是正式的记号，只是表达一个递归过程。

虽然模型没有见过“the lazy+fox”的组合，但它可以通过“lazy+fox”和“+fox”来平滑。

Hierarchical Chinese Restaurant Processes

类似于中餐馆过程，作者提出了一种从Hierarchical Pitman-Yor语言模型采样单词的方法，同时将${G_{\mathbf{u}}}$ marginalize out。

将每个${G_{\mathbf{u}}}$视作当前单词的分布，由于${G_{\mathbf{u}}}$由PY过程产生，所以可以用中餐馆过程从中采样句子。根据Hierarchical Pitman-Yor的定义，唯一需要的是父节点的${G_{\pi(\mathbf{u})}}$，如此递归直到到达根节点$G_0$。这个过程叫做Hierarchical Chinese Restaurant Processes，再来看如何把$G$ marginalize out。

对每个上文$\mathbf{u}$，记从${G_{\mathbf{u}}}$中独立同分布地采样了一个单词序列 ${x_{{{\mathbf{u}}_1}}},{x_{{{\mathbf{u}}_2}}}, \cdots$ ，另有从父节点 ${G_{\pi ({\mathbf{u}})}}$ 独立同分布采样到的${y_{{{\mathbf{u}}_1}}},{y_{{{\mathbf{u}}_2}}}, \cdots$。使用$l$和$k$来分别作为从${G_{\mathbf{u}}}$和${G_{\pi ({\mathbf{u}})}}$采样的单词的下标。如果${y_{{\mathbf{u}}k}} = w$，则记${t_{{\mathbf{u}}wk}} = 1$，否则${t_{{\mathbf{u}}wk}} = 0$（餐馆$\mathbf{u}$中第$k$个桌子是否提供$w$）。定义${c_{{\mathbf{u}}wk}}$表示从${G_{\mathbf{u}}}$采样到的${x_{{\mathbf{u}}l}}$赋值给${y_{{\mathbf{u}}k}}$的次数（餐馆$\mathbf{u}$中提供$w$的餐桌中第$k$个桌子上的人数）。用点表示marginal counts。比如$c_{\mathbf{u} \cdot k}$是${x_{{\mathbf{u}}l}}$赋值给${y_{{\mathbf{u}}k}}$的次数（两者相等的次数）；$c_{\mathbf{u} w \cdot }$是$x_{\mathbf{u} l}=w$的次数（餐馆$\mathbf{u}$中提供$w$的餐桌上的总人数），$t_{\mathbf{u} \cdot \cdot }$是从${G_{\pi(\mathbf{u})}}$采样到的${y_{{\mathbf{u}}k}}$的个数（餐馆$\mathbf{u}$中桌子的总数）。记号有些多，但规律是$c$表示顾客数，而$t$表示桌子数或客人上桌的次数。

这个过程满足如下性质：

$$\left\{ \begin{equation} \begin{aligned}
 {t_{{\mathbf{u}}w \cdot }} = 0\qquad \;{\kern 1pt} \qquad \;{\kern 1pt} {\text{if }}{c_{{\mathbf{u}}w \cdot }} = 0; \hfill  \\
 1 \leqslant {t_{{\mathbf{u}}w \cdot }} \leqslant {{\text{c}}_{{\mathbf{u}}w \cdot }}\qquad {\text{if }}{c_{{\mathbf{u}}w \cdot }} > 0; \hfill  \\
\end{aligned} \end{equation}  \right.$$

$$\begin{equation} \begin{aligned}  {c_{{\mathbf{u}}w \cdot }} &= \sum\limits_{{\mathbf{u'}}:\pi ({\mathbf{u'}}) = {\mathbf{u}}} {{t_{{\mathbf{u'}}w \cdot }}}  \hfill  \\   \hfill  \\ \end{aligned} \end{equation} $$

解释如下：

比如，对于$\mathbf{u}={lazy}, w=fox$，上图fox只有一个table $\mathbf{u} '={that,lazy}$，有${t_{{\mathbf{u}}w \cdot }} = 3$，这里的$\cdot$一共包含$6$个下标，其中$3$个为$1$，$3$个为$0$。${{\text{c}}_{{\mathbf{u}}w \cdot }} = 3$。

如果在上图的基础上生成“that lazy fox”，那么会在the餐馆下新开一个fox餐桌，上面坐一个人。

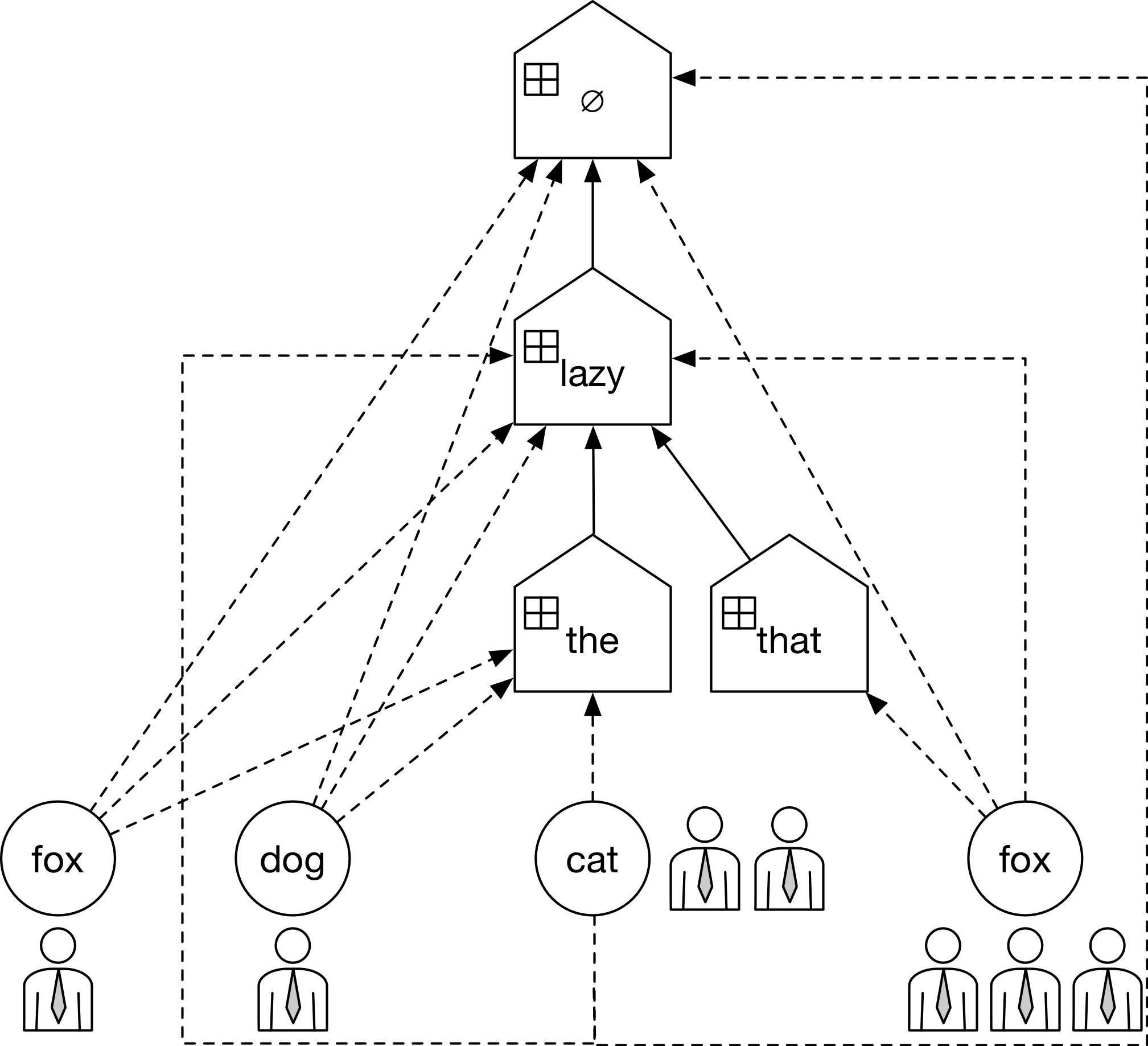
${t_{{\mathbf{u'}}w \cdot }}=1$（the lazy fox）或${t_{{\mathbf{u'}}w \cdot }}=3$（that lazy fox * 3），而${c_{{\mathbf{u}}w \cdot }}=4$（the lazy fox, that lazy fox * 3）。

给定上文$\mathbf{u}$，Hierarchical Pitman-Yor语言模型生成下一个单词的过程如下：

画圈部分使得一个上文$\mathbf{u}$产生$w$后，$\mathbf{u}$会更容易产生$w$。

其实无论是$DP$, $CRP$还是$PYP$，都在生成与base distribution相似的分布。

训练

训练数据$\mathcal{D}$由长$n-1$的上文$\mathbf{u}$和对应的$w$词频${c_{{\mathbf{u}}w \cdot }}$组成。这等效于从${G_{\mathbf{u}}}$中观测到${c_{{\mathbf{u}}w \cdot }}$次$w$。我们想要学习latent vectors ${\mathbf{G}} = \left\{ {{G_{\mathbf{v}}}:{\text{all contexts }}{\mathbf{v}}} \right\}$和参数$\Theta  = \left\{ {{\theta _m},{d_m}:0 \leqslant m \leqslant n - 1} \right\}$：

$$\begin{equation} \begin{aligned}
 p({\mathbf{G}},\Theta |\mathcal{D}) &= \frac{{p({\mathbf{G}},\Theta ,\mathcal{D})}}{{p(\mathcal{D})}} \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

上一章HPYP通过hierarchical CRP来marginalize所有$G_\mathbf{u}$，将其替换为对应餐馆的入座情况$S_\mathbf{u}$。记${\mathbf{S}} = \left\{ {{S_{\mathbf{v}}}:{\text{all contexts }}{\mathbf{v}}} \right\}$，则上面的后验概率转化为：

$$\begin{equation} \begin{aligned}
 p({\mathbf{S}},\Theta |\mathcal{D}) &= \frac{{p({\mathbf{S}},\Theta ,\mathcal{D})}}{{p(\mathcal{D})}} \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

给定上文$\mathbf{u}$，预测下个单词$w$的概率：

$$\begin{equation} \begin{aligned}
 p(w|{\mathbf{u}},\mathcal{D}) &= \int {{\color{red} p(w|{\mathbf{u}},{\mathbf{S}},\Theta } )}{\color{blue}p({\mathbf{S}},\Theta |\mathcal{D})}d({\mathbf{S}},\Theta ) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

红色是某个上文对应的入座与模型参数下的概率，蓝色是在所有入座与模型参数上的平均。

这里的积分通过从$p({\mathbf{S}},\Theta |\mathcal{D})$采样${\left\{ {{{\mathbf{S}}^{(i)}},{\Theta ^{(i)}}} \right\}^I}_{i = 1}$来实现：

$$\begin{equation} \begin{aligned}
 p(w|{\mathbf{u}},\mathcal{D}) \approx \mathop \sum \limits_{i = 1}^I p\left( {w|{\mathbf{u}},{{\mathbf{S}}^{(i)}},{\Theta ^{(i)}}} \right) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

其中$p\left( {w|{\mathbf{u}},{\mathbf{S}},\Theta } \right)$已经在WordProb中定义了：

$$\begin{equation} \begin{aligned}
 p\left( {w|0,{\mathbf{S}},\Theta } \right) &= \frac{1}{V} \hfill  \\
 p\left( {w|{\mathbf{u}},{\mathbf{S}},\Theta } \right) &= \frac{{{c_{{\mathbf{u}}w \cdot }} - {d_{|{\mathbf{u}}|}}{t_{{\mathbf{u}}w \cdot }}}}{{{\theta _{|{\mathbf{u}}|}} + {c_{{\mathbf{u}} \cdot  \cdot }}}} + \frac{{{\theta _{|{\mathbf{u}}|}} + {d_{|{\mathbf{u}}|}}{t_{{\mathbf{u}} \cdot  \cdot }}}}{{{\theta _{|{\mathbf{u}}|}} + {c_{{\mathbf{u}} \cdot  \cdot }}}}p(w|\pi ({\mathbf{u}}),{\mathbf{S}},\Theta ) \hfill  \\
  \hfill  \\
\end{aligned} \end{equation} $$

模型参数$\left\{ {{\mathbf{S}},\Theta } \right\}$通过Gibbs sampling得到，这是一种在联合分布中，通过给定除某个参数外的其它参数采样该参数，重复若干遍直到收敛的算法。详细参考“A Bayesian Interpretation of Interpolated Kneser-Ney”。

References

[1]Y. W. Teh, “A Hierarchical Bayesian Language Model Based On Pitman-Yor Processes.,” arXiv, 2006.

 知识共享署名-非商业性使用-相同方式共享：码农场 » A Hierarchical Bayesian Language Model based on Pitman-Yor Processes