N最短路径的Java实现与分词应用

前言

今天连查带抄地用Java实现了N最短路径，马上要用到自己的分词器里了。

N最短路径其实就是K最短路径（KSP）的变种，KSP指的是DAG中单源路径中前K条最短的路径。求解KSP的算法有删除算法、改进的删除算法（MS Algorithm）、递归枚举算法(REA, Recursive Enumeration Algorithm)，一直到近十年都有人在研究KSP的改进算法以及新算法。

NShortPath最终求出来的路径也不一定是N条，这里实现的并不是上述算法中的任何一种，而是从SharpICTCLAS中分离出来的“NShortPath”算法。

图

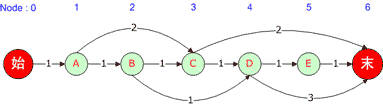
一般图的表示用邻接矩阵记录从顶点from指向顶点to的权值为cost的边，用一维数组记录顶点的下标，比如

// 从顶点from指向顶点to的权值为cost的边
struct edge
{
	int to, cost;
	edge(){}
	edge(int to, int cost)
	{
		this->to = to;
		this->cost = cost;
	}
};

// 边
vector<edge> G[MAX_V];

但是在NShortPath中，需要记录的是到节点to都有哪些节点from。比如上图中，需要关注的是到4号节点D都有哪些边，这些边的起点与花费都记下来，这一步的最终结果是：

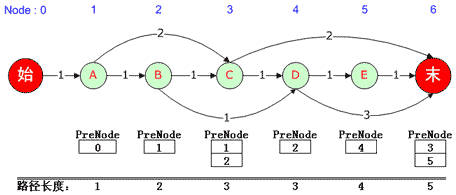
这是原作者 吕震宇的图，有一处需要说明一下，最后一个节点的前驱本来有3个，图中少了一个4，为什么呢？这是因为在到达最后一个节点的路径中，路径最短（1-NShortPath）的路径有两条，4不在路径的节点里面。【注：本文大量使用原作者 吕震宇的的图以及讲解，同时加入自己的理解与代码，注解了不少容易误解的地方（比如作者将“栈”误做“堆栈”，事实上堆是堆，栈是栈），下文不再赘述。】

有了这张图的结果，然后才能进行下一步NShortPath求解。

NShortPath

基本思想

我觉得NShortPath的基本思想是Dijkstra算法的变种，拿1-最短路来说吧，先Dijkstra求一次最短路，然后沿着最短路的路径走下去，只不过在走到某个节点的时候，检查到该节点在路径上的下一个节点是否还有别的路到它（从PreNode查），如果有，就走这些别的路中的没走过第一条（它们都是最短路上的途径节点）。然后推广到N-最短路，N-最短路中PreNode有N个，分别对应n-最短路时候的PreNode，就这么简单。

图解

再谈PreNode的准备

需要为每个顶点维护一个最小堆，最小堆里储存的是边的花费，每条边的终点是这个顶点。还需要维护到每个顶点的前N个最小路径的花费：

 /**
     * 每个顶点的前N个最短路径前驱起点
     */
    private CQueue[][] PreNode;
    /**
     * 到每个顶点的前N个最短路径上的花费之和
     */
    private double[][] weightArray;

回忆一下Dijkstra求最短路的时候，我们只需记录一个最短路的累计花费就行了:

/**
     * 到每个顶点的最短路径上的花费之和
     */
    private double[] weightArray;

这与此处的N-最短路径显著不同。

在遍历图的时候，与Dijkstra最短路径不同，N-最短路径从第二个节点开始，需要将当前节点可能到达的边根据累积第i短长度+该边的长度之和排序记录到PreNode队列数组中，排序由CQueue完成的。

然后从CQueue出队，这样路径长度就是升序了，按顺序更新 weightArray[当前节点][第几短路]就行了。

另外CQueue是一个不同于普通队列的队列，它维护了一个当前指针（下图的蓝色部分），这个蓝色指针在求解第i短路径的时候会用到。

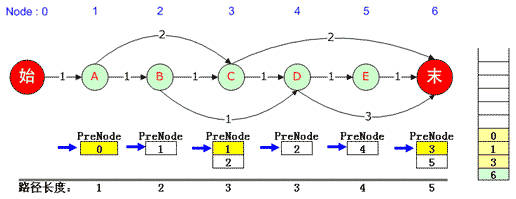
假定看到这里，算法已经计算出了正确的PreNode队列，下面讨论如何从PreNode中找出N最短路径的确切途经节点集合。

1-最短路径的求解

整个计算过程维护了一个路径栈，对于上图来说，

1）首先将最后一个元素压入栈（本例中是6号结点），什么时候这个元素弹出栈，什么时候整个任务结束。

2）对于每个结点的PreNode队列，维护了一个当前指针，初始状态都指向PreNode队列中第一个元素。这个指针是由CQueue维护的，严格来讲不属于算法关心的问题。

3）从右向左依次取出PreNode队列中的当前元素（当前元素出队）并压入栈，并将队列指针重新指向队列中第一个元素。如上图：6号元素PreNode是3，3号元素PreNode是1，1号元素PreNode是0。

4）当第一个元素压入栈后，输出栈内容即为一条队列。本例中0, 1, 3, 6便是一条最短路径。

5）将栈中的内容依次弹出，每弹出一个元素，就将当时压栈时该元素对应的PreNode队列指针下移一格。如果到了末尾无法下移，则继续执行第5步（也就是继续出栈），如果仍然可以移动，则执行第3步。

对于本例，先将“0”弹出栈，在路径上0的下一个是1，得出该元素对应的是1号“A”结点的PreNode队列，该队列的当前指针已经无法下移，因此继续弹出栈中的“1” ；同理该元素对应3号“C”结点，因此将3号“C”结点对应的PreNode队列指针下移。由于可以移动，因此将队列中的2压入队列，2号“B”结点的PreNode是1，因此再压入1，依次类推，直到0被压入，此时又得到了一条最短路径，那就是0，1，2，3，6。如下图：

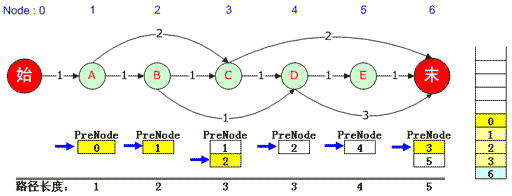
再往下，0、1、2都被弹出栈，3被弹出栈后，由于它对应的6号元素PreNode队列记录指针仍然可以下移，因此将5压入堆栈并依次将其PreNode入栈，直到0被入栈。此时输出第3条最短路径：0, 1, 2, 4, 5, 6。如下图：

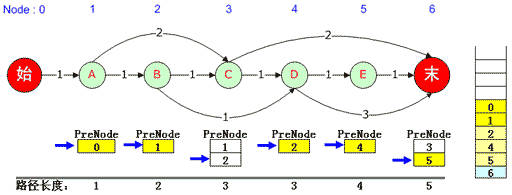
输出完成后，紧接着又是出栈，此时已经没有任何栈元素对应的PreNode队列指针可以下移，于是堆栈中的最后一个元素6也被弹出栈，此时输出工作完全结束。我们得到了3条最短路径，分别是：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

推广到N-最短路

N-最短路中PreNode有N个，分别对应n-最短路时候的PreNode，也就是当前路径是第n短的时候，当前节点对应的PreNode队列。

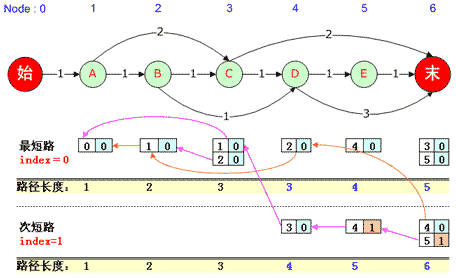
在该图中，观察黄颜色的路径长度表格，到达1号、2号、3号结点的路径虽然有多条，但长度只有一种长度，但到达4号“D”结点的路径长度有两种，即长度可能是3也可能是4，此时在“最短路”处（index＝0）记录长度为3时的PreNode，在“次短路”处（index＝1）处记录长度为4时的PreNode，依此类推。

值得注意的是，此时用来记录PreNode的坐标已经由前文求“1-最短路径”时的一个数（ParentNode值)变为2个数（ParentNode值以及index值）。

如上图所示，到达6号“末”结点的次短路径有两个ParentNode，一个是index=0中的4号结点，一个是index=1的5号结点，它们都使得总路径长度为6。

当N=2时，我们求得了2-最短路径，路径长度有两种，分别长度为5和6，而路径总共有6条，如下：

最短路径：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

========================

次短路径

0, 1, 2, 4, 6,

0, 1, 3, 4, 5, 6,

0, 1, 2, 3, 4, 5, 6,

N-最短路的Java实现

由于这是给公司做的商业分词器，所以不能给出完整的代码。现在该分词器已经全面开源，完整代码请下载http://www.hankcs.com/nlp/hanlp.html。

事实上，C#和Java是如此地像，完全可以自己从SharpICTCLAS中移植一个。

调用程序：

package com.hankcs;

import com.hankcs.KShortPath.Graph;
import com.hankcs.KShortPath.NShortPath;

import java.util.List;

public class Main
{
    public static void main(String[] args)
    {
        Graph graph = new Graph(new String[]{"始##始", "商", "商品", "品", "和", "和服", "服", "服务", "务", "末##末"});
        graph.connect(0, 1, 4.18);
        graph.connect(0, 2, 4.18);
        graph.connect(1, 3, 12.06);
        graph.connect(2, 4, 3.59);
        graph.connect(3, 4, 12.44);
        graph.connect(2, 5, 9.63);
        graph.connect(3, 5, 12.44);
        graph.connect(4, 6, 5.70);
        graph.connect(4, 7, 5.14);
        graph.connect(5, 8, 14.22);
        graph.connect(6, 8, 12.54);
        graph.connect(7, 9, 4.95);
        graph.connect(8, 9, 13.66);
        graph.printByFrom();
        graph.printByTo();
        NShortPath nShortPath = new NShortPath(graph, 3);
        List<int[]> nPaths = nShortPath.getNPaths();
        for (int[] path : nPaths)
        {
            System.out.println(graph.parsePath(path));
        }
    }
}

输出：

========按起点打印========
from:  0, to:  1, weight:04.18, word:始##始@商
from:  0, to:  2, weight:04.18, word:始##始@商品
from:  1, to:  3, weight:12.06, word:商@品
from:  2, to:  4, weight:03.59, word:商品@和
from:  2, to:  5, weight:09.63, word:商品@和服
from:  3, to:  4, weight:12.44, word:品@和
from:  3, to:  5, weight:12.44, word:品@和服
from:  4, to:  6, weight:05.70, word:和@服
from:  4, to:  7, weight:05.14, word:和@服务
from:  5, to:  8, weight:14.22, word:和服@务
from:  6, to:  8, weight:12.54, word:服@务
from:  7, to:  9, weight:04.95, word:服务@末##末
from:  8, to:  9, weight:13.66, word:务@末##末
========按终点打印========
to:  1, from:  0, weight:04.18, word:始##始@商
to:  2, from:  0, weight:04.18, word:始##始@商品
to:  3, from:  1, weight:12.06, word:商@品
to:  4, from:  2, weight:03.59, word:商品@和
to:  4, from:  3, weight:12.44, word:品@和
to:  5, from:  2, weight:09.63, word:商品@和服
to:  5, from:  3, weight:12.44, word:品@和服
to:  6, from:  4, weight:05.70, word:和@服
to:  7, from:  4, weight:05.14, word:和@服务
to:  8, from:  5, weight:14.22, word:和服@务
to:  8, from:  6, weight:12.54, word:服@务
to:  9, from:  7, weight:04.95, word:服务@末##末
to:  9, from:  8, weight:13.66, word:务@末##末
[Vertex{word='始##始'}, Vertex{word='商品'}, Vertex{word='和'}, Vertex{word='服务'}, Vertex{word='末##末'}]
[Vertex{word='始##始'}, Vertex{word='商'}, Vertex{word='品'}, Vertex{word='和'}, Vertex{word='服务'}, Vertex{word='末##末'}]
[Vertex{word='始##始'}, Vertex{word='商品'}, Vertex{word='和'}, Vertex{word='服'}, Vertex{word='务'}, Vertex{word='末##末'}]

Reference

http://www.cnblogs.com/zhenyulu/articles/672442.html

http://blog.csdn.net/sharpdew/article/details/446510

 知识共享署名-非商业性使用-相同方式共享：码农场 » N最短路径的Java实现与分词应用