《算法导论》矩阵链乘法Java实现

问题

有A₁A₂…A_n共n个矩阵，第i个矩阵的大小为p_i-1*p_i，计算代价由标量乘法决定，求最小代价及运算顺序。

比如：

对应的答案是：

 15125次乘法

思路

设m[i,j]表示从i到j的矩阵链的最小计算代价，s[i,j]=k表示在i和j中间的矩阵k后面加一个括号，则m的递推方法是：

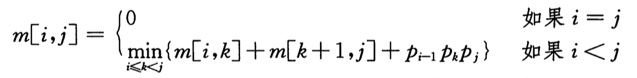
第一项是前半部分，第二项是后半部分，第三项是前后两部分组合的计算代价。最终m[1,n]就是最小代价。由于是ijk三重遍历，所以复杂度是O(n³)。这只是粗略估计，据《算法导论》介绍，准确的复杂度是。

在递推的同时，记录最小的k即可。那如何利用s[i,j]来得到最终的的运算顺序呢？递归往下打括号就行了：

Java实现

import java.util.Scanner;

public class MatrixChainOrder
{
    private static int n;
    private static int[][] m = new int[100][100];
    private static int[][] s = new int[100][100];
    private static int[] p = new int[105];
    private static final int MAX = Integer.MAX_VALUE;

    public static void main(String[] args)
    {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        for (int i = 0; i <= n; i++)
        {
            p[i] = scan.nextInt();
            m[i][i] = 0;
        }

        for (int l = 2; l <= n; l++)
        {
            for (int i = 1; i <= n - l + 1; i++)
            {
                int j = i + l - 1;
                m[i][j] = MAX;
                for (int k = i; k <= j - 1; k++)
                {
                    int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                    if (q < m[i][j])
                    {
                        m[i][j] = q;
                        s[i][j] = k;
                    }
                }
            }
        }
        print(1, n);
        System.out.printf(" %d\n", m[1][n]);
    }

    public static void print(int i, int j)
    {
        if (i == j)
            System.out.print("A" + i);
        else
        {
            System.out.print("(");
            print(i, s[i][j]);
            print(s[i][j] + 1, j);
            System.out.print(")");
        }
    }
}

输入

6
30
35
15
5
10
20
25

输出

((A1(A2A3))((A4A5)A6)) 15125

Reference

http://blog.sina.com.cn/s/blog_9075354e0101o4w4.html

 知识共享署名-非商业性使用-相同方式共享：码农场 » 《算法导论》矩阵链乘法Java实现