![]()

星际穿越:20XX年,11区发明了一种革命性的星际运输技术。其细节如下——
首先空间被降维为二维:
物质在原点(1,1)处被分解为单位质点,每个质点被给予不同的能量波。能量波是由VH两种信号构成的序列,V代表横坐标加一,H代表纵坐标加一。
然后,宇宙中存在多个虫洞,会影响质点的运动轨迹。
当物质进入虫洞入口时,会瞬间被传送到该虫洞的出口。第i个虫洞的坐标是(ai, bi), (ci, di),且满足ai ≤ ci, bi ≤ di, (ai, bi) ≠ (ci, di)。
最后,同时到达终点的质点将被组合为原物质。
你是宇航局的首席程序员,请计算在K个虫洞的空间中,往(N, M)最多能够同时运送多大质量的物质?答案数量级可能很大,请对1,000,000,007求余。
4.1更加复杂的数学问题
计数
终于逃离Burnside的魔爪了 ,但还是离不开题解
,但还是离不开题解
题目其实是求到达某一点的所有方案数,如果不考虑虫洞的话就相当简单,答案是组合数CN+MN。
设起点为s,质点只能往右上走,所以——
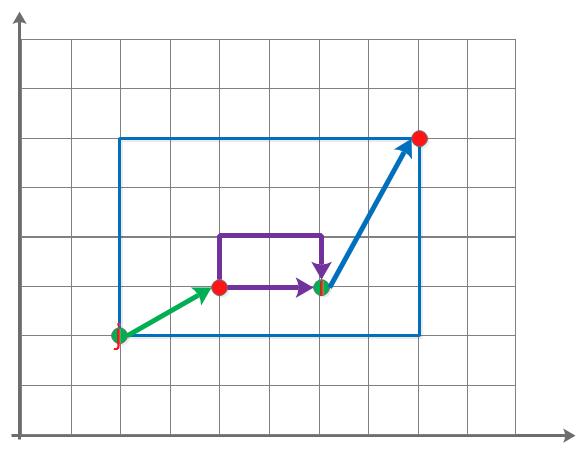
当某个点p左下有虫洞的起点b的时候,到达它的路径数就减少s->b->p。
当某个点p左下有虫洞的终点e的时候,到达它的路径数就增加s->b->e->p。
于是定义dp[i] := 到第i个虫洞入口时的方案数,将虫洞排序后顺序递推即可(此时由于按b递增,s与b之间没有虫洞的干扰,就可以直接用组合数算了)。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
#define MOD 1000000007
inline int add(int a, int b)
{ return (a + b) % MOD; }
inline int sub(int a, int b)
{ return (a - b + MOD) % MOD; }
inline int mul(int a, int b)
{ return 1LL * a * b % MOD; }
// 虫洞
struct warp
{
int x1, y1, x2, y2;
bool operator<(const warp &w) const
{
if (x1 != w.x1)
return x1 < w.x1;
return y1 < w.y1;
}
};
// return d = gcd(a, b) = ax + by
int extgcd(int a, int b, int &x, int &y)
{
int g = a;
x = 1;
y = 0;
if (b != 0)
g = extgcd(b, a % b, y, x), y -= a / b * x;
return g;
}
// 求a的逆元
int inv(int a)
{
int x, y;
extgcd(a, MOD, x, y);
return (MOD + x % MOD) % MOD;
}
int fact[200010]; // 阶乘n!
void init_factorial()
{
fact[0] = 1;
for (int i = 0; i < 200000; ++i)
fact[i + 1] = mul(fact[i], i + 1);
}
// 组合数(从n个序列空位中挑出k个)
inline int nck(int n, int k)
{ return mul(mul(fact[n], inv(fact[n - k])), inv(fact[k])); }
int N, M, K, dp[100010];
// dp[i] := 到第i个虫洞入口时的方案数
vector<warp> warps;
inline int calc(int x1, int y1, int x2, int y2) // 无虫洞模式下s到t的方案数
{
if (x2 < x1 or y2 < y1)
return 0;
return nck(x2 - x1 + y2 - y1, x2 - x1);
}
int solve()
{
memset(dp, 0, sizeof(dp));
sort(begin(warps), end(warps));
warps.push_back((warp) {N, M, N + 1, M + 1});
for (int i = 0; i <= K; ++i)
{
dp[i] = nck(warps[i].x1 + warps[i].y1, warps[i].y1);
for (int j = 0; j < i; ++j)
{
dp[i] = add(dp[i], mul(dp[j], sub(calc(warps[j].x2, warps[j].y2, warps[i].x1, warps[i].y1), // j的终点到i的起点(紫色)
calc(warps[j].x1, warps[j].y1, warps[i].x1, warps[i].y1)))); // j的起点到i的起点
}
}
return dp[K];
}
bool input()
{
warps.clear();
scanf("%d%d%d", &N, &M, &K);
--N;
--M;
int a, b, c, d;
for (int i = 0; i < K; ++i)
{
scanf("%d%d%d%d", &a, &b, &c, &d);
warps.push_back((warp) {a - 1, b - 1, c - 1, d - 1});
}
return N + 1 or M + 1 or K;
}
int main()
{
init_factorial();
while (input())
cout << solve() << endl;
return 0;
}

解决AOJ无法登陆
近期AOJ无法登陆,症状为点击login无反应。打开控制台一看原来是引用了Google和Twitter的js库:
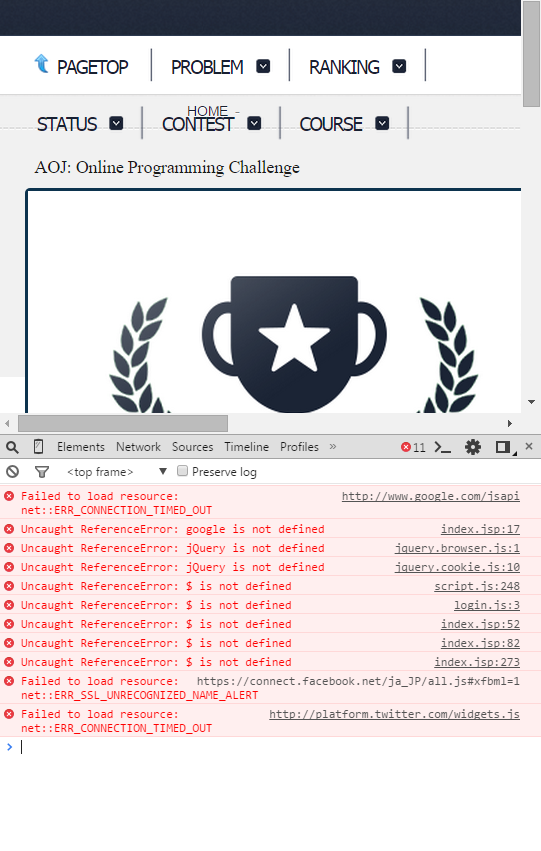
解决方案只有科学上网,呵呵,终于发展到连刷题都要借助梯子的地步了
Reference
http://algoogle.hadrori.jp/aoj/2214/
 码农场
码农场
唉,完全看不懂。