GCJ 2009 World Finals B : Min Perimeter 题解《挑战程序设计竞赛》

GCJ 2009 World Finals B : Min Perimeter 

极小三角：从n个点中找出3个，使其形成的三角形周长最小。

4.6划分、解决、合并：分治法 

平面上的分治法 

不断地用垂直分割线把所有点按x坐标分为左右两半，那么极小三角形的顶点无非三种情况：

1. 同属左边

2. 同属右边

3. 分属两边

通过不断地递归拆分子问题，总能将情况1和2拆分为情况3。所以只需考虑第三种情况。（我只想到了这一步，接下来的限定条件参考了analysis）

假设某个子问题的解是p，那么该子问题递归返回到母问题后，母问题就有一个上界p了。由于所有实际要解决的问题都是情况3，情况3中三点分属两边。

于是这三个点在水平和垂直方向都必须满足一些约束，才能成为最优解。

任何一个点离垂直分割线的距离必须小于p/2，否则周长大于p。

另外，最顶端的点离最底端的点的y坐标差必须小于p/2，否则周长大于p。

这两个约束实际上构成了一个高度为p/2，宽度为p的矩形框。我们将底端与三角形的第一个顶点对齐，只有矩形框内的点才有可能成为另两个顶点，枚举即可。

比如周长等于p的极端情况1

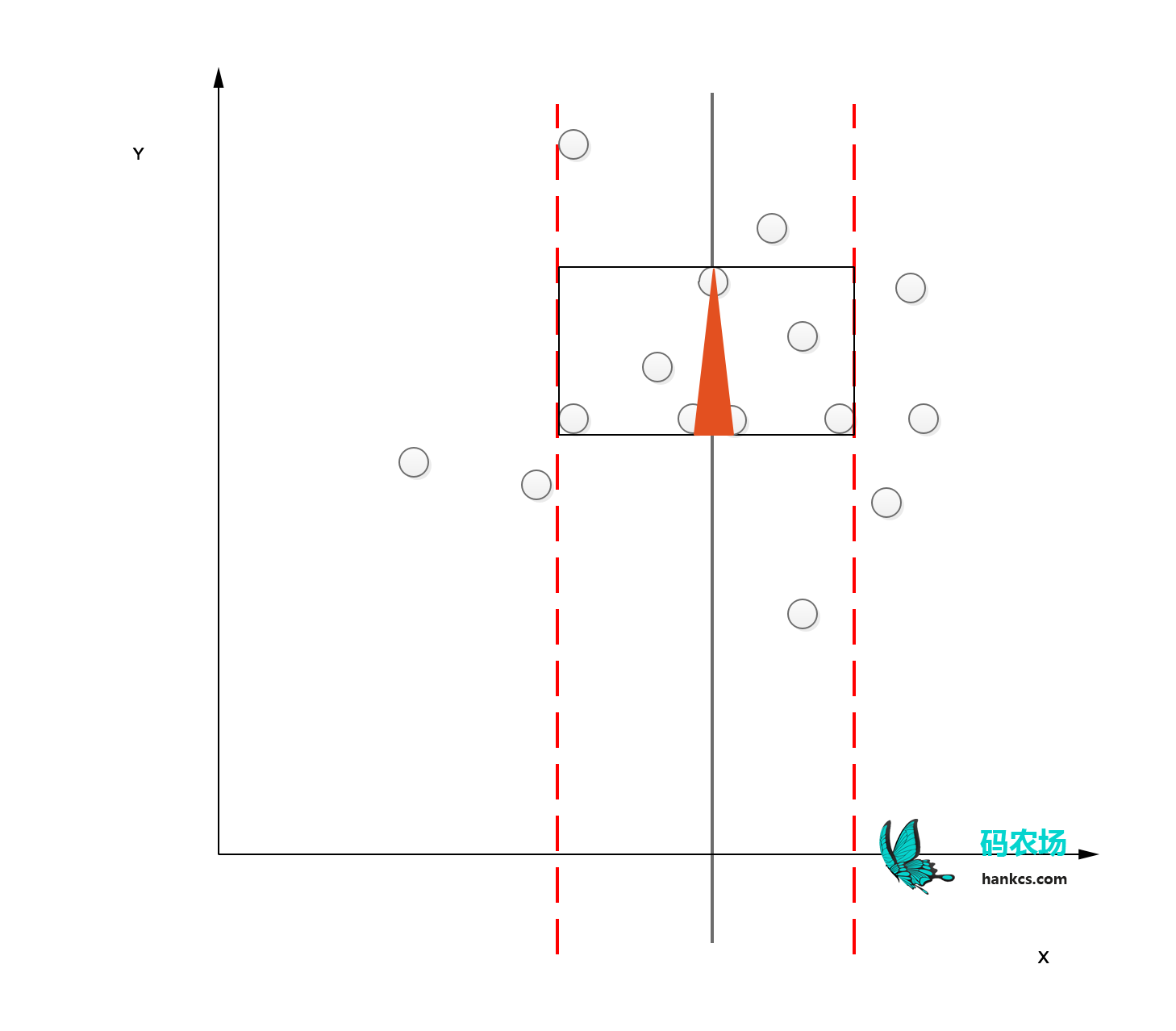
极端情况2

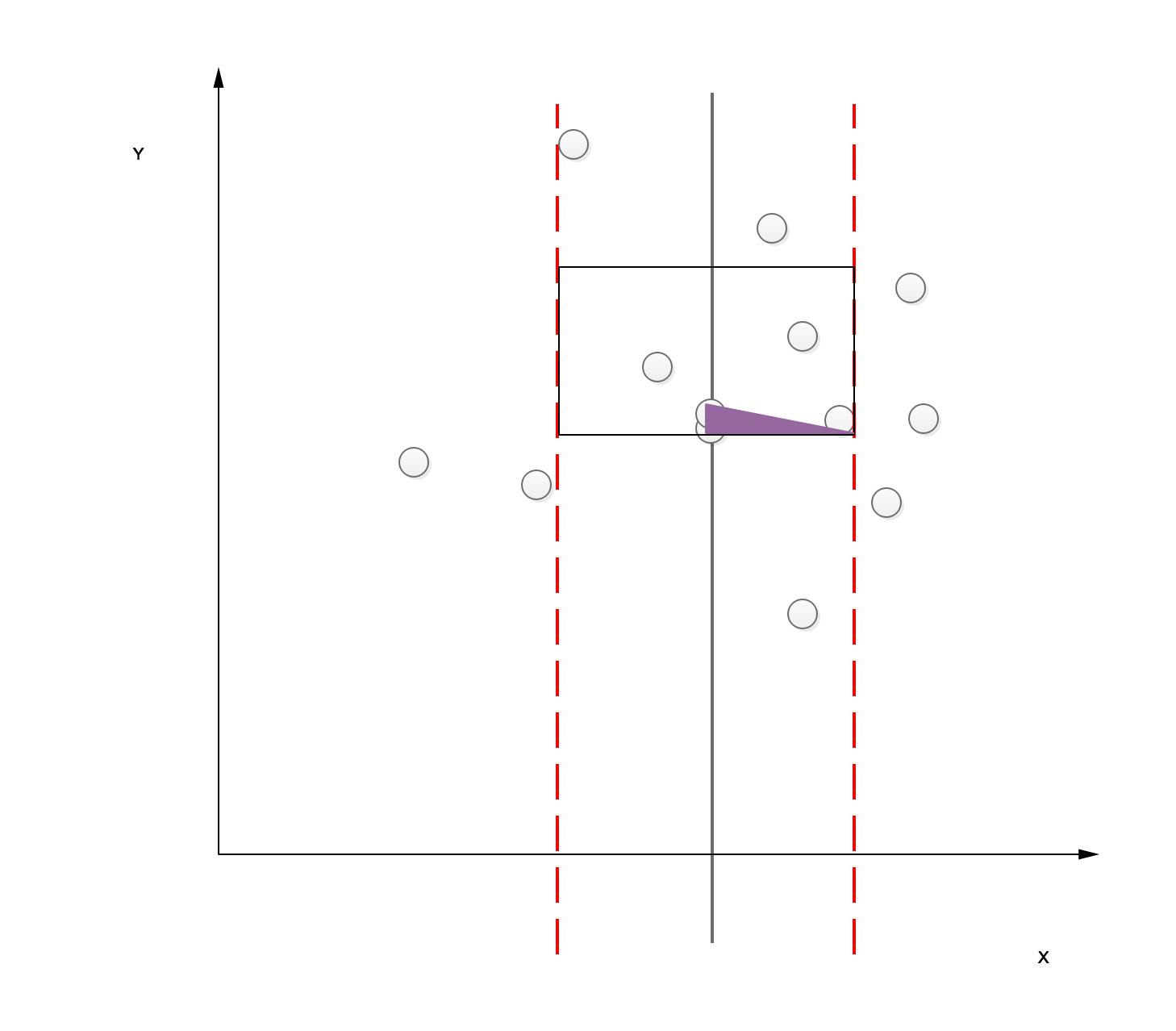
代码

#include <algorithm>
#include <cassert>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <iostream>

using namespace std;
#define REP(i, n) for(int i=0;i<(n);++i)

template<class T>
inline int size(const T &c)
{ return c.size(); }

const int BILLION = 1000000000;
const double INF = 1e20;
typedef long long LL;

struct Point
{
    int x, y;

    Point()
    {}

    Point(int x, int y) : x(x), y(y)
    {}
};

inline Point middle(const Point &a, const Point &b)
{
    return Point((a.x + b.x) / 2, (a.y + b.y) / 2);
}

struct CmpX
{
    inline bool operator()(const Point &a, const Point &b)
    {
        if (a.x != b.x)
            return a.x < b.x;
        return a.y < b.y;
    }
} cmpx;

struct CmpY
{
    inline bool operator()(const Point &a, const Point &b)
    {
        if (a.y != b.y)
            return a.y < b.y;
        return a.x < b.x;
    }
} cmpy;

inline LL sqr(int x)
{ return LL(x) * LL(x); }

inline double dist(const Point &a, const Point &b)
{
    return sqrt(double(sqr(a.x - b.x) + sqr(a.y - b.y)));
}

inline double perimeter(const Point &a, const Point &b, const Point &c)
{
    return dist(a, b) + dist(b, c) + dist(c, a);
}

double calc(int n, const Point points[], const vector<Point> &pointsByY)
{
    if (n < 3)
        return INF;
    int left = n / 2;
    int right = n - left;
    Point split = middle(points[left - 1], points[left]);
    vector<Point> pointsByYLeft, pointsByYRight;
    pointsByYLeft.reserve(left);
    pointsByYRight.reserve(right);
    REP(i, n)
    {
        if (cmpx(pointsByY[i], split))
            pointsByYLeft.push_back(pointsByY[i]);
        else
            pointsByYRight.push_back(pointsByY[i]);
    }
    double res = INF;
    res = min(res, calc(left, points, pointsByYLeft));
    res = min(res, calc(right, points + left, pointsByYRight));
    static vector<Point> closeToTheLine;    // 单线程，静态避免创建与销毁
    int margin = (res > INF / 2) ? 2 * BILLION : int(res / 2);
    closeToTheLine.clear();
    closeToTheLine.reserve(n);
    int start = 0;
    for (int i = 0; i < n; ++i)
    {
        Point p = pointsByY[i];
        if (abs(p.x - split.x) > margin)    // 横向离分割线距离p/2以内
            continue;
        while (start < size(closeToTheLine) && p.y - closeToTheLine[start].y > margin)
            ++start;                        // 纵向离底部p
        for (int i = start; i < size(closeToTheLine); ++i)
        {
            for (int j = i + 1; j < size(closeToTheLine); ++j)
            {
                res = min(res, perimeter(p, closeToTheLine[i], closeToTheLine[j]));
            }
        }
        closeToTheLine.push_back(p);
    }
    return res;
}

double calc(vector<Point> &points)
{
    sort(points.begin(), points.end(), cmpx);
    vector<Point> pointsByY = points;
    sort(pointsByY.begin(), pointsByY.end(), cmpy);
    return calc(size(points), &points[0], pointsByY);
}

int main()
{
    freopen("out.txt", "w", stdout);
    fprintf(stderr, "Solving\n");
    FILE *f = fopen("large.in", "r");
    int ntc;
    fscanf(f, "%d", &ntc);
    REP(tc, ntc)
    {
        int n;
        fscanf(f, "%d", &n);
        vector<Point> points;
        points.reserve(n);
        REP(i, n)
        {
            int x, y;
            fscanf(f, "%d%d", &x, &y);
            points.push_back(Point(2 * x - BILLION, 2 * y - BILLION));  // 先乘2，避免待会儿的除法
        }
        double res = calc(points);
        printf("Case #%d: %.15e\n", tc + 1, res / 2);
    }
    fclose(f);
    fclose(stdout);
}

另外谷歌的测试数据太有范了，下载下来是个Java源码。要求自己编译运行，生成相应的数据。

mv B-small-practice.in Input.java
javac Input.java
java -Xmx512M Input >small.in
head small.in 
15
3
4 5
0 2
10 7
3
268 316
762 378
235 349
3
mv -f B-large-practice.in Input.java
javac Input.java                    
java -Xmx512M Input >large.in       
head large.in 
15
3
433599513 355423475
809635166 973778610
456904466 563063040
4
1000000000 1000000000
1000000000 0
0 1000000000
0 0
ll -h *.in
225M large.in
2.0M small.in

真凶残

 知识共享署名-非商业性使用-相同方式共享：码农场 » GCJ 2009 World Finals B : Min Perimeter 题解《挑战程序设计竞赛》