最长公共子串、最长公共子序列的Java实现与NLP应用

前言

以前HanLP使用“最短编辑距离”来做推荐器，效果有待提高，主要缺点是根据拼音序列的编辑距离推荐的时候，同音字交错很常见，而编辑距离却不那么大。这时我就在寻求一种补充的评分算法，去评判两个句子在拼音这一维度上的相似程度。

最终决定导入最长公共子串和最长公共子序列作为补充。

区别

最长公共子串（Longest Common Substring）指的是两个字符串中的最长公共子串，要求子串一定连续。

最长公共子序列（Longest Common Subsequence）指的是两个字符串中的最长公共子序列，不要求子序列连续。

求解

两者的求解与编辑距离一样，都是动态规划，用空间换时间。

最长公共子串（Longest Common Substring）

设串A长度la，设串B长度lb，定义dp[i][j] = t （0<=i<la, 0<=j<lb，当A[i] = B[j]的时候t是1，否则是0）。那么对角线上连续的1就代表着一个公共字串，取其中最长的就是解了。

举个例子，对于"bab"和"caba"来讲，dp数组如下所示：

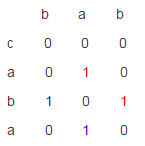
要统计对角线的长度的话，在实现上有些麻烦，不如采取一个策略，将dp定义稍作修改，当A[i] = B[j]的时候，让dp[i][j]=dp[i-1][j-1]+1，于是就可以省略一维数组：

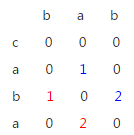
对角线的长度就是上图对角线连续部分的最后一个元素了。于是我们只要一个数组就可以代替上述矩阵，定义new_dp[i] = 第i条对角线的长度，又由于对角线是对称的，所以这个数组的长度只要取la和lb中最长的那个就行了。这样空间复杂度是O（n）。

递推关系是这种感觉：

举个复杂一点的例子

A=www.hankcs.com

B=hankcs

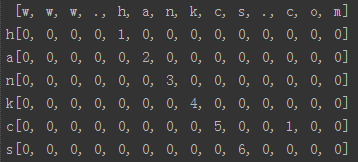
在储存上，只需要一维数组记录一行，然后递推下一行即可。

 [w, w, w, ., h, a, n, k, c, s, ., c, o, m]
h[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
a[0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0]
n[0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0]
k[0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 0]
c[0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 1, 0, 0]
s[0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 0, 0, 0, 0]

还可以继续优化吗？

当然可以，注意到递推关系dp[i][j]=dp[i-1][j-1]+1，每个元素只需要知道它的左上角的值就行，而左上角又取决于左上角的左上角……所以可以一次顺着一条对角线算完一条对角线，然后计算右上或左下（取决于la和lb哪个长）的哪条对角线就行了。这样空间复杂度是O(1)，常数复杂度！

递推关系是这种感觉：

Java代码

/**
 * 求最长公共子串的长度
 *
 * @author hankcs
 */
public class LongestCommonSubstring
{
    public static int compute(char[] str1, char[] str2)
    {
        int size1 = str1.length;
        int size2 = str2.length;
        if (size1 == 0 || size2 == 0) return 0;

        // the start position of substring in original string
        int start1 = -1;
        int start2 = -1;
        // the longest length of common substring
        int longest = 0;

        // record how many comparisons the solution did;
        // it can be used to know which algorithm is better
        int comparisons = 0;

        for (int i = 0; i < size1; ++i)
        {
            int m = i;
            int n = 0;
            int length = 0;
            while (m < size1 && n < size2)
            {
                ++comparisons;
                if (str1[m] != str2[n])
                {
                    length = 0;
                }
                else
                {
                    ++length;
                    if (longest < length)
                    {
                        longest = length;
                        start1 = m - longest + 1;
                        start2 = n - longest + 1;
                    }
                }

                ++m;
                ++n;
            }
        }

        // shift string2 to find the longest common substring
        for (int j = 1; j < size2; ++j)
        {
            int m = 0;
            int n = j;
            int length = 0;
            while (m < size1 && n < size2)
            {
                ++comparisons;
                if (str1[m] != str2[n])
                {
                    length = 0;
                }
                else
                {
                    ++length;
                    if (longest < length)
                    {
                        longest = length;
                        start1 = m - longest + 1;
                        start2 = n - longest + 1;
                    }
                }

                ++m;
                ++n;
            }
        }
        System.out.printf("from %d of str1 and %d of str2, compared for %d times\n", start1, start2, comparisons);
        return longest;
    }

    public static int longestCommonSubstring(String str1, String str2)
    {
        return compute(str1.toCharArray(), str2.toCharArray());
    }
}

测试

package com.hankcs.test.algorithm;

import com.hankcs.hanlp.algoritm.LongestCommonSubstring;
import junit.framework.TestCase;

public class LongestCommonSubstringTest extends TestCase
{
    String a = "www.hankcs.com";
    String b = "hankcs";
    public void testCompute() throws Exception
    {
        System.out.println(LongestCommonSubstring.compute(a.toCharArray(), b.toCharArray()));
        assertEquals(6, LongestCommonSubstring.compute(a.toCharArray(), b.toCharArray()));
    }

    public void testLongestCommonSubstring() throws Exception
    {
        System.out.println(LongestCommonSubstring.longestCommonSubstring(a, b));
        assertEquals(6, LongestCommonSubstring.longestCommonSubstring(a, b));
    }
}

输出

from 4 of www.hankcs.com and 0 of hankcs, compared for 84 times
6

最长公共子序列（Longest Common Substring）

定义 dp[i][j] = A[从0到i]和B[从0到j]的LCS，那么就有

           0                            (如果i=0且j=0)
dp[i][j] = dp[i-1][j-1] + 1            （如果i和j>0，且A[i]=B[j]）
           max(dp[i][j-1], dp[i-1][j]) （如果i和j>0，且A[i]!=B[j]）

Java代码

package com.hankcs.hanlp.algoritm;

/**
 * @author hankcs
 */
public class LongestCommonSubsequence
{
    public static int compute(char[] str1, char[] str2)
    {
        int substringLength1 = str1.length;
        int substringLength2 = str2.length;

        // 构造二维数组记录子问题A[i]和B[j]的LCS的长度
        int[][] opt = new int[substringLength1 + 1][substringLength2 + 1];

        // 从后向前，动态规划计算所有子问题。也可从前到后。
        for (int i = substringLength1 - 1; i >= 0; i--)
        {
            for (int j = substringLength2 - 1; j >= 0; j--)
            {
                if (str1[i] == str2[j])
                    opt[i][j] = opt[i + 1][j + 1] + 1;// 状态转移方程
                else
                    opt[i][j] = Math.max(opt[i + 1][j], opt[i][j + 1]);// 状态转移方程
            }
        }
        System.out.println("substring1:" + new String(str1));
        System.out.println("substring2:" + new String(str2));
        System.out.print("LCS:");

        int i = 0, j = 0;
        while (i < substringLength1 && j < substringLength2)
        {
            if (str1[i] == str2[j])
            {
                System.out.print(str1[i]);
                i++;
                j++;
            }
            else if (opt[i + 1][j] >= opt[i][j + 1])
                i++;
            else
                j++;
        }
        System.out.println();
        return opt[0][0];
    }

    public static int compute(String str1, String str2)
    {
        return compute(str1.toCharArray(), str2.toCharArray());
    }
}

测试

public class LongestCommonSubsequenceTest extends TestCase
{
    String a = "Tom Hanks";
    String b = "Hankcs";
    public void testCompute() throws Exception
    {
        System.out.println(LongestCommonSubsequence.compute(a, b));
    }
}

输出

substring1:Tom Hanks
substring2:Hankcs
LCS:Hanks
5

NLP应用

在搜索引擎中，用户输入一个词，搜索引擎会推荐一些备选Query。特别地，当用户输入汉语拼音的时候，主流搜索引擎也会推荐出相应的中文来：

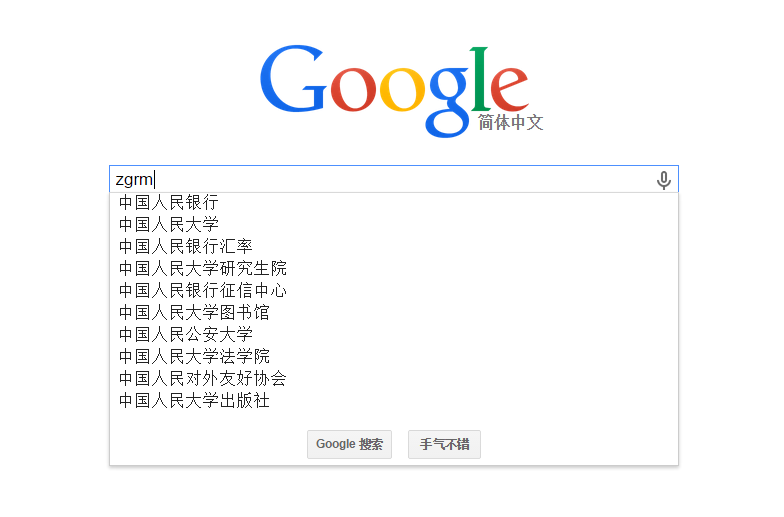
甚至在中文和拼音混合的情况下，也能智能推荐出合理的词条来：

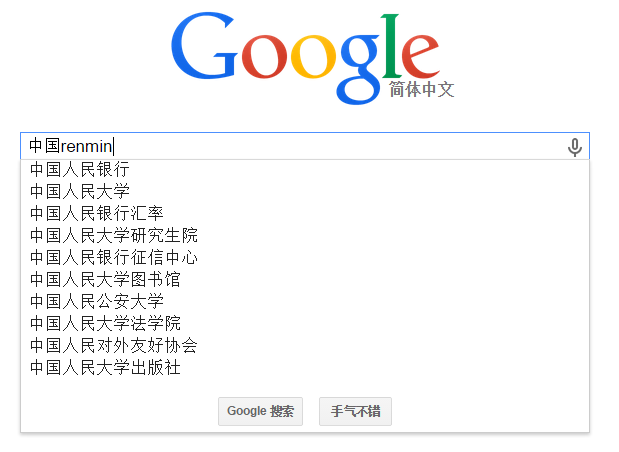
声母和拼音混合，一样可以:

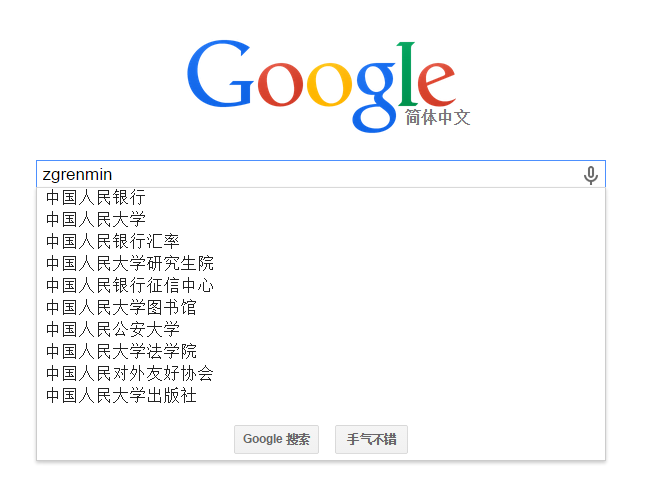
在HanLP中，我也实现了相同的功能，能够根据拼音的相似程度作出智能推荐：

中国人民 [中国人民, 中国人民共和国, 中国人民武装警察部队上海市, 中国人民解放军中华人民共和国, 中国人民解放军热爱, 中国软件, 全国人民, 养护工人们, 最高荣誉, 体会工人们] 180ms
zhongguorenmin [中国人民, 中国人民共和国, 中国人民武装警察部队上海市, 中国人民解放军中华人民共和国, 中国人民解放军热爱, 中国软件, 全国人民, 养护工人们, 最高荣誉, 体会工人们] 66ms
zgrm [中国人民共和国, 中国人民解放军中华人民共和国, 中国人民武装警察部队上海市, 中国人民解放军热爱, 中国人民, 组织个人, 最高荣誉, 副主任张光人, 体会工人们, 个人梦想] 22ms
zgrenmin [中国人民, 全国人民, 中国人民解放军热爱, 中国人民武装警察部队上海市, 中国人民共和国, 中国人民解放军中华人民共和国, 静安人民, 全市人民, 发展人民, 常德人民] 35ms
中国renmin [中国人民, 中国人民共和国, 中国人民武装警察部队上海市, 中国人民解放军中华人民共和国, 中国人民解放军热爱, 中国软件, 全国人民, 养护工人们, 最高荣誉, 体会工人们] 39ms
租房 [一直租房, 办理廉租房, 是否公租房, 组团走访, 宁市走访, 服务走访, 上门走访, 进行走访, 主动走访, 一行走访] 36ms
就医 [做起旧衣, 实现就业, 登记就业, 社区就业, 初步就业, 增强就业, 任职就业, 未婚就业, 安置就业, 新增就业] 33ms
孩子上学 [汉字书写, 标准试行, 工作事项, 知识宣传, 地址陕西, 中实新村, 住所修改, 行政事项, 听证事项, 保护知识产权] 39ms
教室资格 [教师资格, 会计技术资格, 教师职工, 建设总公司, 净水作坊, 上海市职工, 建设智慧, 公司职工, 落实整改, 中凯城市之光] 34ms

值得一提的是，当用户不小心输入了“教室资格”的时候，HanLP能够智能地校正输入错误为“教师资格”：

Reference

http://my.oschina.net/leejun2005/blog/117167

http://www.cnblogs.com/ider/p/longest-common-substring-problem-optimization.html

 知识共享署名-非商业性使用-相同方式共享：码农场 » 最长公共子串、最长公共子序列的Java实现与NLP应用