POJ 1180 Batch Scheduling​ 题解《挑战程序设计竞赛》

POJ 1180 Batch Scheduling 

批任务调度：N个顺序任务，分别耗时Ti，权重Fi。 若批处理，每批任务耗时S+T_i之和，同批次任务视作同时完成。总耗时等于每个任务完成的时刻乘以其权重，求最少耗时？

4.4常用技巧精选（二） 

双端队列 

最朴素的思路就是dp了，定义

dp[i] := 从任务i到N的最少耗时

从后往前递推，有状态转移方程

dp[j] = min(dp[j], t * f + dp[j + i]);

其中f是从j到N的F之和，相对于i来讲是个常量。t是从j到N的T之和，随着i增加。

看起来是个O(n²)的糟糕算法，也的确会TLE。

但擦亮眼睛，剑走偏锋，题目的数据范围给的很清楚

1 <= N <= 10000
0 <= S <= 50
1 <= Ti <= 100

S最多相当于一个批次执行时间的1/200，暗示着一个批次不会超过200个任务。于是限制一下搜索分支，就水过去了。

#include <iostream>
using namespace std;
const int MAX_N = 10000 + 8;
int S, N;
int T[MAX_N], F[MAX_N];
int sum_F[MAX_N];
int dp[MAX_N];
int solve()
{
    for (int j = N - 1; j >= 0; --j)
    {
        int f = sum_F[N] - sum_F[j], t = S;
        for (int i = 1; j + i <= N && i <= 200; i++)
        {
            t += T[j + i - 1];
            dp[j] = min(dp[j], t * f + dp[j + i]);
        }
    }
    return dp[0];
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%d%d", &N, &S);
    memset(dp, 0x3f, N * sizeof(int));
    for (int i = 0; i < N; ++i)
    {
        scanf("%d%d", T + i, F + i);
        sum_F[i + 1] = sum_F[i] + F[i];
    }
    printf("%d\n", solve());
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

想走正道的话，老老实实地用双端队列吧。

定义

dp[i] := 从 1 ~ i 的最小耗时贡献

这里贡献的意思是，假设任务i到N存在但是T=0，任务1到i的最小耗时。比如说假设一共2个任务，每个任务独占一个批次

dp[1] = (f1+f2)*t1+S*(f1+f2)
dp[2] = min{dp[1] + f2*(t1+t2), dp[1] + f2*t2} = dp[1] + f2*t2

这个min的意思是，有两个分支，前者将两个任务放到一个批次中，后者放到两个批次中。

虽然看起来没什么规律，但我们稍微变一下形式

sum_F[i] := F的前i项之和，同理定义sum_T
dp[0] = 0
dp[1] = (sum_F[N)-sum_F[0])*sum_T[1]+dp[0]+(S-sum_T[0])*(sum_F[N]-sum_F[0])
dp[2] = (sum_F[N)-sum_F[1])*sum_T[2]+dp[1]+(S-sum_T[1])*(sum_F[N]-sum_F[1])

就能抽象出一条直线来：

dp[i] = min{k[1~i]*sum_T[1~i]+b[1~i]}
k[i] = sum_F[N] - sum_F[i-1]
b[i] = dp[i-1]+(S-sum_T[i-1])*(sum_F[N]-sum_F[i-1])

其实蛮好理解的，假设dp[i]->dp[j]，那么k[i]*sum_T[1~i]表示1~i-1的T都会累积到i~N的任务上去，这还不够，还需要加上b[i]。b[i]中的dp[i-1]是前i-1个任务的最小耗时贡献，后面是一个对贡献的修正。

上面的dp方程跟书上是类似的

dp[i]=S[i]+min{fj(i)|0≤j≤i-k}

其中f是关于dp的直线方程，直接利用书上的结论就行了。

#include <iostream>
#include <deque>

using namespace std;

// (k, b) := 直线kx+b
struct Line
{
    int k, b;

    Line(int k, int b) : k(k), b(b)
    {}
};

const int MAX_N = 10000 + 8;
int N;
int S;
int sum_T[MAX_N];
int sum_F[MAX_N];
int dp[MAX_N];              // dp[i] := 从 1 ~ i 的最小耗时贡献


int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%d%d", &N, &S);
    for (int i = 1; i <= N; i++)
    {
        scanf("%d%d", sum_T + i, sum_F + i);
        sum_T[i] += sum_T[i - 1];
        sum_F[i] += sum_F[i - 1];
    }
    deque<Line> lines;
    lines.push_back(Line(sum_F[N], S * sum_F[N]));
    for (int i = 1; i <= N; i++)
    {
        int k1, b1;
        int k2, b2;
        int k3, b3;

        while (lines.size() > 1)
        {
            k1 = lines[0].k;
            b1 = lines[0].b;
            k2 = lines[1].k;
            b2 = lines[1].b;
            if (k1 * sum_T[i] + b1 >= k2 * sum_T[i] + b2)
                lines.pop_front();  // 若头部的值不是最小值了则删去
            else
                break;
        }

        k1 = lines[0].k;
        b1 = lines[0].b;
        dp[i] = k1 * sum_T[i] + b1;
        k3 = sum_F[N] - sum_F[i];
        b3 = dp[i] + (S - sum_T[i]) * (sum_F[N] - sum_F[i]);

        while (lines.size() > 1)
        {
            k1 = lines[lines.size() - 2].k;
            b1 = lines[lines.size() - 2].b;
            k2 = lines[lines.size() - 1].k;
            b2 = lines[lines.size() - 1].b;
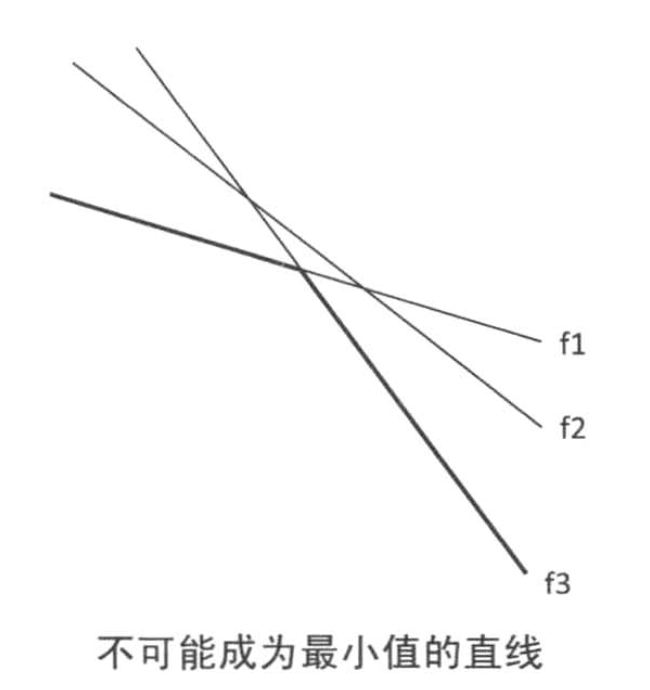
            if ((k2 - k1) * (b3 - b2) >= (b2 - b1) * (k3 - k2)) // tail不可能成为最小值的直线
                lines.pop_back();
            else
                break;
        }

        lines.push_back(Line(k3, b3));
    }

    printf("%d\n", dp[N]);
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

虽然从运行时间上来看并无卵用。

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1180 Batch Scheduling​ 题解《挑战程序设计竞赛》