![]()

许愿珠:用红蓝绿三色共n个珠子串成项链,求旋转和翻转后仍不一样的串法种数?
4.1更加复杂的数学问题
计数
虽然是裸的Pólya定理,但属于组合数学的内容,还是少不了自我扫盲。Pólya定理的基础Burnside引理是求解互异的组合状态的个数的方法:

据说该定理的应用比较麻烦,染色问题常用Pólya定理:

其中G={a1 ,…ag} c(ai )为置换gi的循环节数(i=1…s) 。
对应题目的翻转问题,分奇偶讨论。
奇数时,如题图右,对称轴是一个珠子到圆心的连线,一共n条。选定对称轴后,对称轴上的一个珠子构成一个循环,其他n-1个珠子分别以对称轴对称构成(n-1)/2个循环,所以循环节的个数是 1 + (n – 1) / 2 = (n + 1) / 2 。
偶数时,如题图左,对称轴可能是两个珠子的连线,一共 n / 2条。选定对称轴后,对称轴上的两个珠子构成两个循环,其他n-2个珠子分别以对称轴对称构成(n-2)/2个循环;对称轴还可能是两个珠子的中点和圆心的连线,所有珠子两两对称,构成n / 2 个循环。
对应题目的旋转问题,直接套用现成结论。
一共n个置换,第i个置换的循环节的个数为gcd(n, i)。证明详见《挑战程序设计竞赛(第2版)》P302:

有了循环节,接下来只要将循环节数c作为幂求mc即可。值得注意的是,同时考虑了旋转和翻转后,置换群的个数应当是2n。
第一种方法直接暴力枚举k:
#include <iostream>
using namespace std;
#define LL long long
int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
LL power(LL p, LL n)
{
LL sum = 1;
while (n)
{
if (n & 1)
sum *= p;
p *= p;
n /= 2;
}
return sum;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int n; const LL m = 3;
while (~scanf("%d", &n) && n != -1)
{
if (n == 0)
{
puts("0");
continue;
}
LL count = 0;
for (int i = 1; i <= n; ++i)
count += power(m, gcd(i, n));
if (n & 1)
count += n * power(m, n / 2 + 1);
else
count += n / 2 * (power(m, n / 2 + 1) + power(m, n / 2));
count /= n * 2;
printf("%lld\n", count);
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
| 14463727 | hankcs | 1286 | Accepted | 132K | 0MS | C++ | 963B | 2015-07-23 22:03:36 |
第二种方法将相同的gcd合并在一起计算:
#include <iostream>
#include <map>
#include <vector>
using namespace std;
#define LL long long
inline LL power(LL p, LL n)
{
LL sum = 1;
while (n)
{
if (n & 1)
sum *= p;
p *= p;
n /= 2;
}
return sum;
}
//************************************
// Method: divisor
// FullName: divisor
// Access: public
// Returns: vector<int> 约数
// Qualifier: 约数枚举
// Parameter: const int & n 目标数n
//************************************
vector<int> divisor(const int& n)
{
vector<int> res;
for (int i = 1; i * i <= n; ++i)
{
if (n % i == 0)
{
res.push_back(i);
if (i != n / i)
{
res.push_back(n / i);
}
}
}
return res;
}
//************************************
// Method: prime_factor
// FullName: prime_factor
// Access: public
// Returns: map<int, int>
// Qualifier: 整数分解
// Parameter: int n
//************************************
map<int, int> prime_factor(int n)
{
map<int, int> res;
for (int i = 2; i * i <= n; ++i)
{
while (n % i == 0)
{
++res[i];
n /= i;
}
}
if (n != 1)
{
res[n] = 1;
}
return res;
}
LL polya(const int& m, const int& n)
{
map<int, int> primes = prime_factor(n);
vector<int> divs = divisor(n);
LL res = 0;
for (int i = 0; i < divs.size(); ++i)
{
// 求divs[i]的欧拉函数值
LL euler = divs[i];
for (map<int, int>::iterator it = primes.begin(); it != primes.end(); ++it)
{
int p = it->first;
if (divs[i] % p == 0) euler = euler / p * (p - 1);
}
res += euler * power(m, n / divs[i]);
}
// 最后除以n
res /= n;
return res;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int n; const LL m = 3;
while (~scanf("%d", &n) && n != -1)
{
if (n == 0)
{
puts("0");
continue;
}
LL count = polya(m, n) * n;
if (n & 1)
count += n * power(m, n / 2 + 1);
else
count += (power(m, n / 2 + 1) + power(m, n / 2)) * (n / 2);
count /= 2 * n;
printf("%lld\n", count);
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
| 14463721 | hankcs | 1286 | Accepted | 148K | 0MS | C++ | 2202B | 2015-07-23 22:01:40 |
似乎题目的数据量并不大,没有区分度。
Reference
第14-15讲_Burnside引理与Polya定理
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 1286 Necklace of Beads 题解《挑战程序设计竞赛》
知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 1286 Necklace of Beads 题解《挑战程序设计竞赛》
 码农场
码农场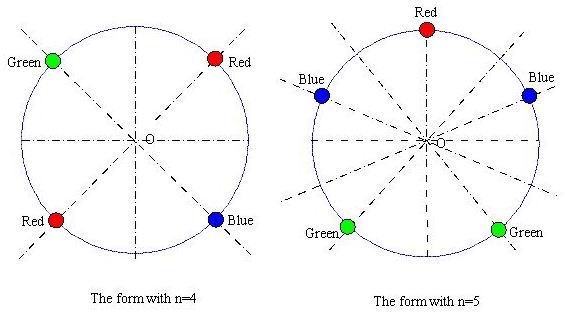
程序设计