POJ 2115 C Looooops 题解《挑战程序设计竞赛》

POJ 2115 C Looooops

循环次数：求for (variable = A; variable != B; variable += C)的循环次数，其中变量为k比特无符号整数。

4.1更加复杂的数学问题 

模运算的世界 

数论真是虐狗。

k位无符号整数溢出会归零，所以问题其实是求模线性方程Cx = B – A (mod 2^k)的最小解。于是参考《算法导论》P528的拓展欧几里得算法和P534的伪码：

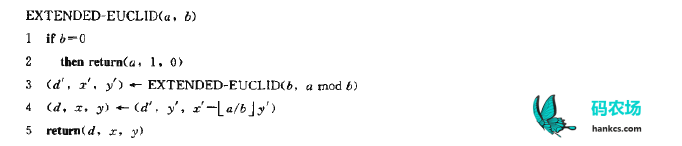
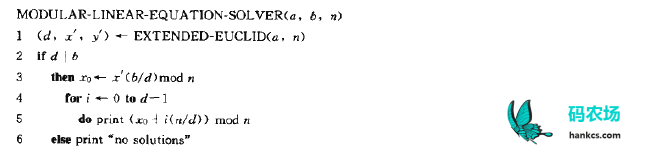
就行了。

正如《算法导论》数论这章的前言所述，数论曾被认为是一门漂亮但却没什么大用处的纯数学学科，现在也是应用在密码学里。所以，我暂时没下定决心花时间在数论算法上面。

#include <cstdio>

typedef long long LL;

// return d = gcd(a, b) = ax + by
inline LL extended_euclid(const LL& a, const LL& b, LL &x, LL &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = extended_euclid(b, a % b, x, y);
    LL x1;
    x1 = x, x = y, y = x1 - a / b * y;
    return d;
}

// return ax = b (mod n) 的最小解
inline LL modular_linear_equation_solver(const LL &a, const LL &b, const LL &n)
{
    LL d, x, y;
    d = extended_euclid(a, n, x, y);    // a 与 n 的最大公约数d
    if (b % d)
        return -1;
    LL x0 = x * (b / d) % n + n;    // x0 * d 是 ax = b (mod n) 的一个解
    return x0 % (n / d);            // ax = b (mod n) 的最小解
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    LL A, B, C, k;
    while (~scanf("%lld%lld%lld%lld", &A, &B, &C, &k), A || B || C || k)
    {
        LL d = modular_linear_equation_solver(C, B - A, 1LL << k);
        if (d == -1)
            puts("FOREVER");
        else
            printf("%lld\n", d);
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2115 C Looooops 题解《挑战程序设计竞赛》