![]()

中央暖气:冬天来了,但URAL大学的暖气系统还没启动。这个暖气系统包括许多阀门,只有所有阀门都打开了才能供应暖气。大学里有一些技术员,他们每人负责一个或多个阀门,有可能存在一个阀门由多个人负责的情况。当一个技术员接到启动暖气系统的指示后他就会把所有自己负责的阀门都转动一次。这意味着如果一个阀门原来是开的,他就把它关掉;如果原来是关的,就把它打开。任何一个技术员的工作都不可能让其他人代劳。
你的任务是决定哪些技术员应接到指示,从而使整个大学的暖气系统启动。注意学校里一共有N个技术员和N个阀门(1 <= N <= 250)。
输入的第一行是一个数字N(1 <= N <= 250)。下面的N行是每一个技术员负责的阀门的列表。其中第i行包含第i个技术员所负责的阀门的编号。每一个阀门列表都以-1结束。
输出满足条件的升序的技术员编号序列。如果有好几个序列满足要求,就输出最短的一个。如果无法找到方法把整个学校的暖气系统启动,就输出"No solution" 。
4.1更加复杂的数学问题
矩阵
线性代数全忘光了,这一章的题目离不开题解啊……好在高斯消元我还有点印象,摘录一份说明:
高斯消元
算法目的:
高斯消元,一般用于求解线性方程组AX = B(或 模线性方程组AX mod P = B),以四个未知数,四个方程为例,AX=B表示成4×4的矩 阵和4×1的矩阵相乘的形式:
其中A和B(b0 b1 b2 b3)已知,要求列向量X(x0 x1 x2 x3)的值。
算法核心思想:
对于n个方程,m个未知数的方程组,消元的具体步骤如下:1、枚举第i (0 <= i < n) 行,初始化列为col = 0,每次从[i, n)行中找到第col列中元素绝对值最大的行和第i行进行交换(找到最大的行是为了在消元的时候把浮点数的误差降到最小);
a) 如果第col列的元素全为0,放弃这一列的处理,col+1,i不变,转1);
b) 否则,对于所有的行j (i < j < n),如果a[j][col]不为0,则需要进行消元,以期第i行以下的第col列的所有元素都消为0(这一步就是线性代数中所说的初等行变换,具体的步骤就是将第j行的所有元素减去第i行的所有元素乘上一个系数,这个系数即a[j][col] / a[i][col])。
2、重复步骤1) 直到n个方程枚举完毕或者列col == m。
3、判断解的情况:
a) 如果出现某一行,系数矩阵全为0,增广矩阵不全为0,则无解(即出现[0 0 0 0 0 b],其中b不等于0的情况);
b) 如果是严格上三角,则表明有唯一解;
c) 如果增广矩阵有k (k > 0)行全为0,那么表明有k个变量可以任意取值,这几个变量即自由变量;对于这种情况,一般解的范围是给定的,令解的取值有T个,自由变量有V个,那么解的个数就是 TV。
算法复杂度:
O(n3)
具体做法是,先将输入处理为01矩阵。题目用例中,如果第i个人管理第j个阀门,则记matrix[j][i] = 1,否则为0。然后目标是让所有闸门都开,也就是B向量都为1,于是得到增广矩阵:
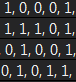
然后高斯消元法得到行梯阵式:
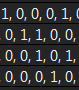
从最后一行往上求解,也就是由尾至头地将已知的答案代入其他等式中的未知数即可。
值得注意的是,本题中是开关运算,也就是将减法改为异或(半加),将乘法改成与运算即可。
另外,似乎题目所有case都有解
#include <iostream>
using namespace std;
#define MAX_N 256
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int matrix[MAX_N][MAX_N]; // 增广矩阵
int ans[MAX_N]; // 解向量
int n;
while (~scanf("%d", &n))
{
int t;
memset(matrix, 0, sizeof(matrix));
memset(ans, 0, sizeof(ans));
for (int i = 1; i <= n; ++i)
{
while (~scanf("%d", &t) && t != -1)
{
matrix[t][i] = 1;
}
matrix[i][n + 1] = 1;
}
for (int i = 1; i <= n; ++i)
{
int col = -1;
for (int j = i; j <= n; ++j) // 从[i, n)行中找到第col列中元素绝对值最大的行记作col
{
if (matrix[j][i])
{
col = j;
break;
}
}
for (int j = i; j <= n + 1; j++)
{
swap(matrix[i][j], matrix[col][j]); // 交换第i行和第col行
}
for (int j = i + 1; j <= n; j++) // 对于所有的行j (i < j < n)
{
if (matrix[j][i]) // 如果m[j][i]不为0,则需要进行消元
{
for (int k = i; k <= n + 1; k++) // 以期第i行以下的第col列的所有元素都消为0
{
matrix[j][k] ^= matrix[i][k]; // 具体的步骤就是将第j行的所有元素减去第i行的所有元素乘上一个系数,这个系数即m[j][col] / m[i][col]
}
}
}
}
for (int i = n; i >= 1; --i) // 行梯阵式
{
ans[i] = matrix[i][n + 1]; // 简化行梯阵式
for (int j = i - 1; j >= 1; --j)
{
matrix[j][n + 1] ^= (ans[i] & matrix[j][i]);// m[j][n+1] -= ans[i] * m[j][i]
}
}
bool first = true;
for (int i = 1; i <= n; i++)
{
if (ans[i])
{
if (first)
{
printf("%d", i);
first = false;
}
else
{
printf(" %d", i);
}
}
}
puts("");
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
| 14348164 | hankcs | 2345 | Accepted | 388K | 47MS | C++ | 1806B | 2015-07-05 21:00:31 |
Reference
http://www.nocow.cn/index.php/Translate:URAL/1042
http://www.cppblog.com/menjitianya/archive/2014/06/08/207226.html
https://zh.wikipedia.org/wiki/%E9%AB%98%E6%96%AF%E6%B6%88%E5%8E%BB%E6%B3%95
https://github.com/Wizmann/ACM-ICPC/blob/master/Timus%20Online%20Judge/1042.cc
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 2345 Central heating 题解《挑战程序设计竞赛》
知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 2345 Central heating 题解《挑战程序设计竞赛》
 码农场
码农场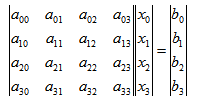
隔壁ACM集训队队员来点个赞,您的题解对我帮助很大!
谢谢~