POJ 2720 Last Digits 题解《挑战程序设计竞赛》

POJ 2720 Last Digits

轮回：定义递归函数f(x) = b^f(x-1) if x > 0, and f(0)=1，给出b和x，求f(x)的最后n位数。

4.1更加复杂的数学问题 

模运算的世界 

不刷一题不足麻醉我幽愤苦楚的心绪。

如果x比较小，则可以直接用防溢出的次方函数来做。否则，则需要利用数论公式：

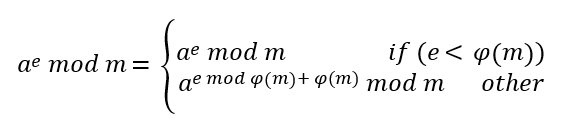
考虑到b和x的范围都固定了，所以可以做一个软cache，以应对题目的多case。

#include <cstring>
#include <cstdio>

using namespace std;

#define MAX_PRIME 2777
#define MAX_N 100 + 1
#define LL long long
int prime[MAX_PRIME], size;     // 素数表
int ten_power[8];               // 十的n次方
int cache[MAX_N][MAX_N];        // 答案表，ans=cache[b][i]
int fbx[MAX_N][MAX_N];          // fb(x)表，fb(x)=fbx[b][x]，如果为-1则超出10e7

// return x^y
int power_of(const int& x, const int& y)
{
    if (y < 0) return -1;
    int p = 1;
    for (int i = 0; i < y; ++i)
    {
        p *= x;
        if (p >= ten_power[7]) return -1;
    }
    return p;
}

// 初始化素数表和一些cache
void prepare()
{
    bool is_prime[MAX_PRIME];
    memset(is_prime, 1, sizeof(is_prime));
    is_prime[0] = is_prime[1] = false;
    for (int i = 2; i < MAX_PRIME; ++i)
    {
        if (is_prime[i])
        {
            prime[size++] = i;
            for (int j = i + i; j < MAX_PRIME; j += i)
            {
                is_prime[j] = false;
            }
        }
    }
    ten_power[0] = 1;
    for (int i = 1; i <= 7; ++i)
    {
        ten_power[i] = ten_power[i - 1] * 10;
    }
    memset(cache, -1, sizeof(cache));
    for (int i = 1; i < MAX_N; ++i)
    {
        fbx[i][0] = 1;
        for (int j = 1; j < MAX_N; ++j)
        {
            fbx[i][j] = power_of(i, fbx[i][j - 1]);
        }
    }
}

//return phi(n) , 复杂度O(sqrt(n))
int phi(int x)
{
    int ret = x;
    for (int i = 2; i * i <= x; i++)
    {
        if (x % i == 0)
        {
            ret = ret / i * (i - 1);
            for (; x % i == 0; x /= i);
        }
    }
    if (x != 1)
    {
        ret = ret / x * (x - 1);
    }
    return ret;
}

// return (a * b) % m
int mod_mult(LL x, int n, int mod)
{
    int ret = 1;
    for (; n; n >>= 1, x = x * x % mod)
    {
        if (n & 1)
        {
            ret = ret * x % mod;
        }
    }
    return ret;
}

// return fb(x) % mod
int solve(int b, int x, int mod)
{
    if (x == 0)
        return 1;
    if (mod == 1)
        return 0;
    if (fbx[b][x] < 0)  // 超出范围，利用公式
    {
        int euler = phi(mod);
        return mod_mult(b,
                        solve(b, x - 1, euler) + euler,// 按照fb(x)的迭代定义和数论公式
                        mod);
    }
    else
    {
        return fbx[b][x] % mod;
    }
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    prepare();

    int b, iteration, n, ans;
    char format[] = "%00d\n";
    while (~scanf("%d", &b) && b)
    {
        scanf("%d%d", &iteration, &n);
        format[2] = char(n + '0');

        if (cache[b][iteration] == -1)
        {
            if (b == 1)
            {
                ans = 1;
            }
            else
            {
                ans = solve(b, iteration, ten_power[7]);
            }
            cache[b][iteration] = ans;
        }
        ans = cache[b][iteration] % ten_power[n];

        printf(format, ans);
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2720 Last Digits 题解《挑战程序设计竞赛》