POJ 2914 Minimum Cut 题解 《挑战程序设计竞赛》

POJ 2914 Minimum Cut

最小割：求无向图的最小割。

3.5借助水流解决问题的网络流

最小割

知道stoer_wagner最小割算法就能做，不知道就做不出来，跟背单词一样，没啥意思。唯一有意思的地方在于stoer_wagner的思想，以及它是怎么来的。

由于无向图不是网络流，没有给定源点s和汇点t，求最小割的时候，朴素算法就是枚举st，但是复杂度太高。

stoer_wagner就想着要偷懒啊，如果G的最小割Cut把G分成M，N两个点集，那么枚举的s和t无非以下两种情况：

①：如果s∈M，t∈N则Min-C（s，t）= Cut（这就是最终的最小割了）

②：如果s，t∈M（或者s，t∈N）则Min-C（s，t）<= Cut（那么合并s和t后并不影响最小割，所以就把st合并了得到中间结果图G'，继续在图G'上求最小割直到命中条件①）

因为利用到了中间结果G'，G'<G，所以降低了复杂度。另外，这个合并的思想有点像Prim最小生成树算法。

至于②中提到的合并操作，定义为Contract(a,b) := 删掉点 a, b 及边(a, b)，加入新节点 c，对于任意 v ∈ 与ab联通的点集，做一条新的边w(v, c) = w(c, v) = w(a, v) + w(b, v) ，比如在下图中执行Contract（5,6）:

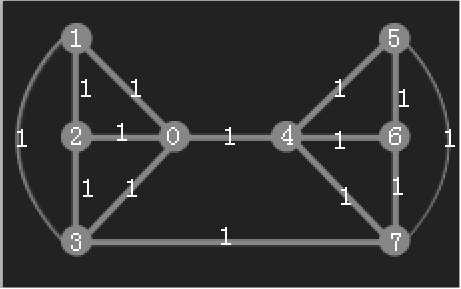
执行后：

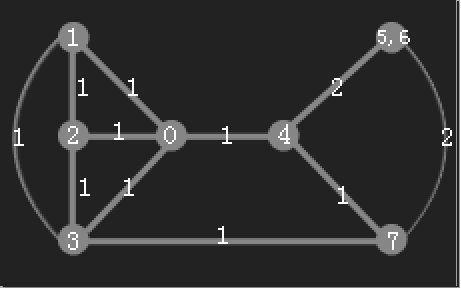
算法步骤如下:

1. 设最小割cut=INF, 任选一个点s到集合A中, 定义W(A, p)为A中的所有点到A外一点p的权总和.

2. 对刚才选定的s, 更新W(A,p)(该值递增).

3. 选出A外一点p, 且W(A,p)最大的作为新的s, 若A!=G(V), 则继续2.

4. 把最后进入A的两点记为s和t, 用W(A,t)更新cut.

5. 合并st，即新建顶点u, 边权w(u, v)=w(s, v)+w(t, v), 删除顶点s和t, 以及与它们相连的边.

6. 若|V|!=1则继续1.

至于算法的证明，请参考《stoerwagner-mincut.[Stoer-Wagner,Prim,连通性,无向图,最小边割集].pdf》。我也许经常用泰勒定理，但是我对它的证明兴趣不大。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define MAX_N 500 + 16
#define INF 0x3f3f3f3f

int G[MAX_N][MAX_N];
int v[MAX_N];			//	v[i]代表节点i合并到的顶点
int w[MAX_N];			//	定义w(A,x) = ∑w(v[i],x)，v[i]∈A
bool visited[MAX_N];	//	用来标记是否该点加入了A集合

int stoer_wagner(int n)
{
	int min_cut = INF;
	for (int i = 0; i < n; ++i)
	{
		v[i] = i;		//	初始还未合并，都代表节点本身
	}
	
	while (n > 1)
	{
		int pre = 0;	//	pre用来表示之前加入A集合的点（在t之前一个加进去的点）
		memset(visited, 0, sizeof(visited));
		memset(w, 0, sizeof(w));
		for (int i = 1; i < n; ++i)
		{
			int k = -1;
			for (int j = 1; j < n; ++j)  //	选取V-A中的w(A,x)最大的点x加入集合
			{
				if (!visited[v[j]])
				{
					w[v[j]] += G[v[pre]][v[j]];
					if (k == -1 || w[v[k]] < w[v[j]])
					{
						k = j;
					}
				}
			}
			
			visited[v[k]] = true;		//	标记该点x已经加入A集合
			if (i == n - 1)				//	若|A|=|V|（所有点都加入了A），结束
			{
				const int s = v[pre], t = v[k];		//	令倒数第二个加入A的点（v[pre]）为s，最后一个加入A的点（v[k]）为t
				min_cut = min(min_cut, w[t]);		//	则s-t最小割为w(A,t)，用其更新min_cut
				for (int j = 0; j < n; ++j)			//	Contract(s, t)
				{
					G[s][v[j]] += G[v[j]][t];
					G[v[j]][s] += G[v[j]][t];
				}
				v[k] = v[--n];						//	删除最后一个点（即删除t，也即将t合并到s）
			}
			// else 继续
			pre = k;
		}
	}
	return min_cut;
}


///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int n, m;
	while (scanf("%d%d", &n, &m) != EOF)
	{
		memset(G, 0, sizeof(G));
		while (m--)
		{
			int u, v, w;
			scanf("%d%d%d", &u, &v, &w);
			G[u][v] += w;
			G[v][u] += w;
		}
		printf("%d\n", stoer_wagner(n));
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

Reference

http://blog.sina.com.cn/s/blog_700906660100v7vb.html

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2914 Minimum Cut 题解 《挑战程序设计竞赛》