POJ 3068 “Shortest” pair of paths 题解 《挑战程序设计竞赛》

POJ 3068 "Shortest" pair of paths

危险品：N个仓库由M条有向边连接，每条边都有一定费用。将两种危险品从0运到N-1，除了起点和终点外，危险品不能放在一起，也不能走相同的路径。求最小费用？

3.5借助水流解决问题的网络流 

最小费用流 

除了起点和终点，不能放一起，说明普通顶点的容量都是1，起点终点容量为2。对所有边,追加容量=1；对起点，增加一个源点，建一条容量为2，费用为0的边，连到起点，对终点，增加一个汇点，从终点建一条容量为2，费用0的边到汇点。如图，对于用例：

2 3
0 1 20
0 1 20
1 0 10

原图：

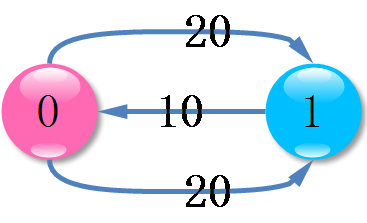
改造为：

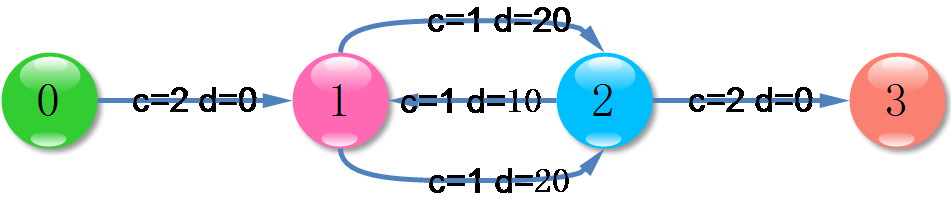
这样就得到了一个网络流，在上面跑F=2的最小费用流即可。

#include <iostream>
#include <vector>
#include <queue>
#include <functional>
using namespace std;

#define INF 0x3f3f3f3f
///////////////////////////////最小费用流开始///////////////////////////////////////////
#define MAX_V 64 + 16
typedef pair<int, int> P;	// first保存最短距离，second保存顶点编号
//用于表示边的结构体
struct edge
{
	int to;		// 终点
	int cap;	// 容量
	int cost;	// 费用
	int rev;	// 反向边
	edge(int to, int cap, int cost, int rev) :to(to), cap(cap), cost(cost), rev(rev){}
};
int V;			// 顶点数
vector<edge> G[MAX_V];	// 图的邻接表
int h[MAX_V];	// 顶点的势
int dist[MAX_V];// 最短距离
int prevv[MAX_V];	// 最短路中的前驱节点
int preve[MAX_V];	// 最短路中的前驱节点对应的边

// 向图中增加一条从from到to的容量为cap费用为cost的边
void add_edge(int from, int to, int cap, int cost)
{
	G[from].push_back(edge( to, cap, cost, G[to].size() ));
	G[to].push_back(edge(from, 0, -cost, G[from].size() - 1));
}

// 求解从s到t流量为f的最小费用流，如果没有流量为f的流，则返回-1
int min_cost_flow(int s, int t, int f)
{
	int res = 0;
	memset(h, 0, sizeof(h));
	while (f > 0)
	{
		// 使用Dijkstra算法更新h
		priority_queue<P, vector<P>, greater<P> > que;
		memset(dist, INF, sizeof(dist));
		dist[s] = 0;
		que.push(P(0, s));
		while (!que.empty())
		{
			P p = que.top(); que.pop();
			int v = p.second;
			if (dist[v] < p.first) continue;
			for (int i = 0; i < G[v].size(); ++i)
			{
				edge &e = G[v][i];
				if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
				{
					dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
					prevv[e.to] = v;
					preve[e.to] = i;
					que.push(P(dist[e.to], e.to));
				}
			}
		}
		if (dist[t] == INF)
		{
			// 不能再增广
			return -1;
		}
		for (int v = 0; v < V; ++v)
		{
			h[v] += dist[v];
		}
		
		// 沿s到t的最短路尽量增广
		int d = f;
		for (int v = t; v != s; v = prevv[v])
		{
			d = min(d, G[prevv[v]][preve[v]].cap);
		}
		f -= d;
		res += d * h[t];
		for (int v = t; v != s; v = prevv[v])
		{
			edge &e = G[prevv[v]][preve[v]];
			e.cap -= d;
			G[v][e.rev].cap += d;
		}
	}
	return res;
}

void clear()
{
	for (int i = 0; i < V; ++i)
	{
		G[i].clear();
	}
}
///////////////////////////////最小费用流结束///////////////////////////////////////////

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int id = 0;
	int N, M;
	while (scanf("%d%d", &N, &M), N && M)
	{
		V = N + 2;
		add_edge(0, 1, 2, 0);
		add_edge(N, N + 1, 2, 0);
		
		for (int i = 0; i < M; ++i)
		{
			int from, to, cost;
			scanf("%d%d%d", &from, &to, &cost);
			++from; ++to;
			add_edge(from, to, 1, cost);
		}
		int min_cost = min_cost_flow(0, N + 1, 2);
		printf("Instance #%d: ", ++id);
		if (min_cost == -1)
		{
			printf("Not possible\n");
		}
		else
		{
			printf("%d\n", min_cost);
		}
		clear();
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3068 “Shortest” pair of paths 题解 《挑战程序设计竞赛》