POJ 3713 Transferring Sylla​ 题解 《挑战程序设计竞赛》

POJ 3713 Transferring Sylla

三连通图：判断一个无向图是否三连通？

3.5借助水流解决问题的网络流

最大流

刷个题报平安，果然无论是主观还是客观我都闲不下来，明天加班！

三连通图指的是去掉3个点就不连通的图，但是并没有直接求三连通的算法。著名的Tarjan算法可以求解连通和割点，再枚举删除一个点就能达到三连通的目的。

先看用例2，是由用例1去掉一条边而变成非三连通图的：

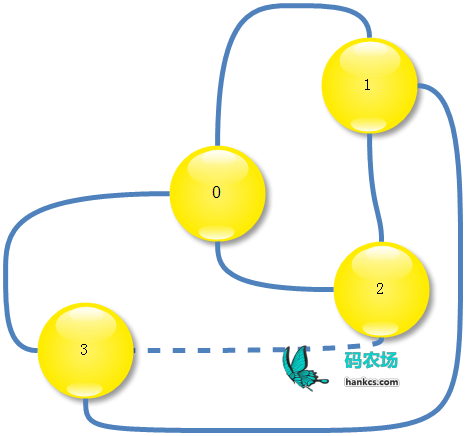
至少造成了2和3非三连通：

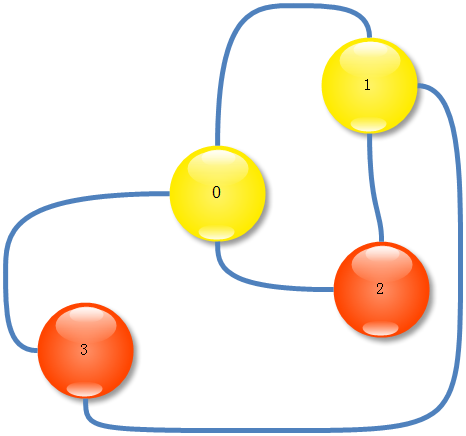
我们来思考如何推导出2和3非三连通，假设从上图中删除了节点0，通过Tarjan算法，我们可以发现节点1是割点：

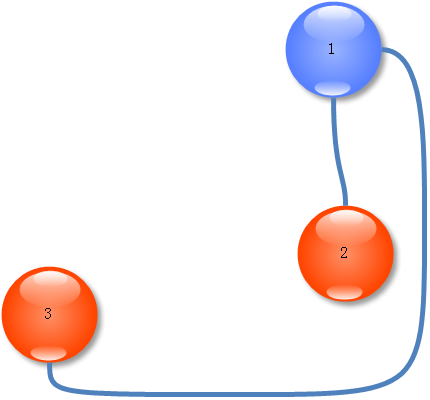
那么只需删除从3到割点和从3到我们枚举删除的节点0的两条边，就可以将3和2分割开来：

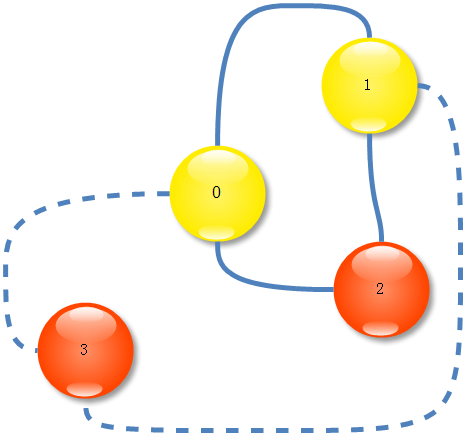
才删除了两条边2和3就不连通了，这个图显然不是三连通图。

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>

using namespace std;

#define MAXN 512

vector<int> G[MAXN];
int V;
bool is_cut_vertex[MAXN];       //  是否是割点
int status[MAXN];               //  0:没有访问 1:正在访问 2:已经访问
int lowlink[MAXN];              //  从i出发经有向边可到达的所有结点中最小的index
int index[MAXN];                //  表示i节点在树中的深度
int root;                       //  根节点
bool has_cut_vertex;            //  是否存在割点

void init(const int &v)
{
    V = v;
    has_cut_vertex = false;
    for (int i = 0; i <= V; ++i)
    {
        G[i].clear();
    }
}


void tarjan_dfs(int current, int from, int depth)
{
    status[current] = 1;  //正在访问
    lowlink[current] = index[current] = depth; // 深度
    int sub_tree = 0; //子树个数
    int v;
    for (vector<int>::const_iterator it = G[current].begin(), end = G[current].end(); it != end; ++it)
    {
        v = *it;
        if (v != from && status[v] == 1)
        {
            lowlink[current] = min(lowlink[current], index[v]);
        }
        if (0 == status[v])
        {
            tarjan_dfs(v, current, depth + 1);
            ++sub_tree; //子树 +1
            lowlink[current] = min(lowlink[current], lowlink[v]);
            //求割点
            if ((current == root && sub_tree > 1) || (current != root && lowlink[v] >= index[current]))
            {
                is_cut_vertex[current] = 1;
                has_cut_vertex = true;
            }
        }
    }
    status[current] = 2;
}

void calc(int del)
{
    memset(is_cut_vertex, 0, sizeof(is_cut_vertex));
    memset(status, 0, sizeof(status));
    memset(lowlink, 0, sizeof(lowlink));
    memset(index, 0, sizeof(index));

    status[del] = 2;
    root = 0;
    if (del == 0)
    {
        root = 1;
    }
    tarjan_dfs(root, -1, 1);
}

//求图是否是三连通
bool solve()
{
    for (int i = 0; i < V; ++i)
    {
        calc(i);
        //判断图是否连通
        for (int j = 0; j < V; ++j)
        {
            if (0 == status[j])
            {
                has_cut_vertex = true;
                break;
            }
        }

        if (has_cut_vertex)
        {
            break;
        }
    }

    return !has_cut_vertex;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    int N, M;
    while (scanf("%d%d", &N, &M) && N)
    {
        init(N);
        for (int _ = 0; _ < M; ++_)
        {
            int from, to;
            scanf("%d%d", &from, &to);
            G[from].push_back(to);
            G[to].push_back(from);
        }
        puts(solve() ? "YES" : "NO");
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

顺便这题没看出来跟最大流有什么关系。

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3713 Transferring Sylla​ 题解 《挑战程序设计竞赛》