放牧代码和思想
专注自然语言处理、机器学习算法
    愛しさ 優しさ すべて投げ出してもいい

POJ 1742 Coins 图表详解 《挑战程序设计竞赛(第2版)》

码农场 > 编程开发 > C++ 2014-02-08 阅读(8993) 评论(3)

POJ 1742 Coins

传说中的男人八题，是男人就A这八题。有n种面额的硬币，面额个数分别为A_i、C_i，求最多能搭配出几种不超过m的金额？

这是一个多重部分和问题(多重背包问题)，放在了《2.3 记录结果再利用的“动态规划” 优化递推关系式》。最基本的做法是：

dp[i][j] := 用前i种硬币能否凑成j

递推关系式：

dp[i][j] = （存在k使得dp[i – 1][j – k * A[i]]为真，0 <= k <= m 且下标合法）

然后三重循环ijk递推

#include <iostream>
#include <algorithm>
using namespace std;

bool dp[100 + 16][100000 + 16]; // dp[i][j] := 用前i种硬币能否凑成j
int A[100 + 16];
int C[100 + 16];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n, m;
	while(cin >> n >> m && n > 0)
	{
		memset(dp, 0, sizeof(dp));
		for (int i = 0; i < n; ++i)
		{
			cin >> A[i];
		}
		for (int i = 0; i < n; ++i)
		{
			cin >> C[i];
		}
		dp[0][0] = true;
		for (int i = 0; i < n; ++i)
		{
			for (int j = 0; j <= m; ++j)
			{
				for (int k = 0; k <= C[i] && k * A[i] <= j; ++k)
				{
					dp[i + 1][j] |= dp[i][j - k * A[i]];
				}
			}
		}
		int answer = count(dp[n] + 1, dp[n] + 1 + m , true); // 总额0不算在答案内
		cout << answer << endl;
	}
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
    system("out.txt");
#endif
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

这种代码不用提交也知道会TLE，因为这个朴素的算法的复杂度是O(m∑iCi)，比如那第二个用例画成图的话会看到：

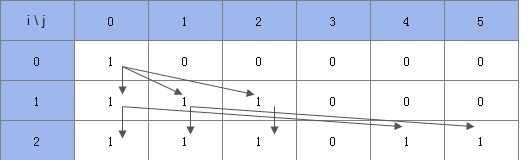
解释一下，dp数组和更新顺序为：

第二个用例：

1 0 0 0 0 0 

0 0 0 0 0 0 

0 0 0 0 0 0 

————–

因为可以用0个1加上dp[0][0]拼成0；所以，dp[1][0]被更新为真

因为可以用1个1加上dp[0][0]拼成1；所以，dp[1][1]被更新为真

因为可以用2个1加上dp[0][0]拼成2；所以，dp[1][2]被更新为真

1 0 0 0 0 0 

1 1 1 0 0 0 

0 0 0 0 0 0 

————–

因为可以用0个4加上dp[1][0]拼成0；所以，dp[2][0]被更新为真

因为可以用0个4加上dp[1][1]拼成1；所以，dp[2][1]被更新为真

因为可以用0个4加上dp[1][2]拼成2；所以，dp[2][2]被更新为真

因为可以用1个4加上dp[1][0]拼成4；所以，dp[2][4]被更新为真

因为可以用1个4加上dp[1][1]拼成5；所以，dp[2][5]被更新为真

1 0 0 0 0 0 

1 1 1 0 0 0 

1 1 1 0 1 1 

————–

4

顺便第一个用例：

1 0 0 0 0 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

————–

因为可以用0个1加上dp[0][0]拼成0；所以，dp[1][0]被更新为真

因为可以用1个1加上dp[0][0]拼成1；所以，dp[1][1]被更新为真

因为可以用2个1加上dp[0][0]拼成2；所以，dp[1][2]被更新为真

1 0 0 0 0 0 0 0 0 0 0 

1 1 1 0 0 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

————–

因为可以用0个2加上dp[1][0]拼成0；所以，dp[2][0]被更新为真

因为可以用0个2加上dp[1][1]拼成1；所以，dp[2][1]被更新为真

因为可以用0个2加上dp[1][2]拼成2；所以，dp[2][2]被更新为真

因为可以用1个2加上dp[1][1]拼成3；所以，dp[2][3]被更新为真

因为可以用1个2加上dp[1][2]拼成4；所以，dp[2][4]被更新为真

1 0 0 0 0 0 0 0 0 0 0 

1 1 1 0 0 0 0 0 0 0 0 

1 1 1 1 1 0 0 0 0 0 0 

0 0 0 0 0 0 0 0 0 0 0 

————–

因为可以用0个4加上dp[2][0]拼成0；所以，dp[3][0]被更新为真

因为可以用0个4加上dp[2][1]拼成1；所以，dp[3][1]被更新为真

因为可以用0个4加上dp[2][2]拼成2；所以，dp[3][2]被更新为真

因为可以用0个4加上dp[2][3]拼成3；所以，dp[3][3]被更新为真

因为可以用0个4加上dp[2][4]拼成4；所以，dp[3][4]被更新为真

因为可以用1个4加上dp[2][1]拼成5；所以，dp[3][5]被更新为真

因为可以用1个4加上dp[2][2]拼成6；所以，dp[3][6]被更新为真

因为可以用1个4加上dp[2][3]拼成7；所以，dp[3][7]被更新为真

因为可以用1个4加上dp[2][4]拼成8；所以，dp[3][8]被更新为真

1 0 0 0 0 0 0 0 0 0 0 

1 1 1 0 0 0 0 0 0 0 0 

1 1 1 1 1 0 0 0 0 0 0 

1 1 1 1 1 1 1 1 1 0 0 

————–

8

这个算法每次只记录一个bool值，损失了不少信息。在这个问题中，不光能够求出是否能得到某个金额，同时还能把得出了此金额时A_i还剩下多少个算出来，这样直接省掉了k那重循环。

优化dp定义：

dp[i][j] := 用前i种硬币凑成j时第i种硬币最多能剩余多少个（-1表示配不出来）
            如果dp[i - 1][j] >= 0(前i-1个数可以凑出j，那么第i个数根本用不着)直接为C[i]
dp[i][j] =  如果j < A[i]或者dp[i][j - a[i]] <=0 (面额太大或者在配更小的数的时候就用光了）-1
            其他（将第i个数用掉一个） dp[i][j-a[i]] - 1

最后统计一下dp数组第n行>=0的个数就知道答案了：

#include <iostream>
#include <algorithm>
using namespace std;

int dp[100 + 16][100000 + 16]; // dp[i][j] := 用前i种硬币凑成j时第i种硬币最多能剩余多少个
int A[100 + 16];
int C[100 + 16];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n, m;
	while(cin >> n >> m && n > 0)
	{
		memset(dp, -1, sizeof(dp));
		dp[0][0] = 0;
		for (int i = 0; i < n; ++i)
		{
			cin >> A[i];
		}
		for (int i = 0; i < n; ++i)
		{
			cin >> C[i];
		}
		for (int i = 0; i < n; ++i)
		{
			for (int j = 0; j <= m; ++j)
			{
				if (dp[i][j] >= 0)
				{
					dp[i + 1][j] = C[i];
				}
				else if (j < A[i]						// 用一个就超出，不能用
						|| dp[i + 1][j - A[i]] <= 0)		// 连凑比j小的数的时候都用完了，此时更加用完了
				{
					dp[i + 1][j] = -1;
				}
				else
				{
					dp[i + 1][j] = dp[i + 1][j - A[i]] - 1;		// 用上了一个第i个硬币
				}
			}
		}
		int answer = count_if(dp[n] + 1, dp[n] + 1 + m , bind2nd(greater_equal<int>(), 0)); // 总额0不算在答案内
		cout << answer << endl;
	}
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
    system("out.txt");
#endif
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

还是拿第二个用例画个图：

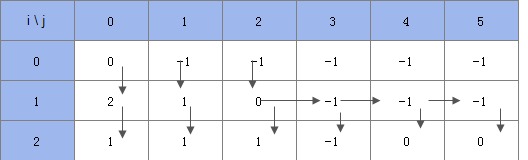
第二个用例：

0 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 

————–

dp[0][0]不为负,dp[1][0]更新为硬币0的个数。

dp[0][1]其他，dp[1][1]更新为dp[1][0]

dp[0][2]其他，dp[1][2]更新为dp[1][1]

dp[1][2]用完了，dp[1][3]更新为硬币0的个数。

dp[1][3]用完了，dp[1][4]更新为硬币0的个数。

dp[1][4]用完了，dp[1][5]更新为硬币0的个数。

0 -1 -1 -1 -1 -1 

2 1 0 -1 -1 -1 

-1 -1 -1 -1 -1 -1 

————–

dp[1][0]不为负,dp[2][0]更新为硬币1的个数。

dp[1][1]不为负,dp[2][1]更新为硬币1的个数。

dp[1][2]不为负,dp[2][2]更新为硬币1的个数。

余额太大，dp[2][3]更新为硬币1的个数。

dp[1][4]其他，dp[2][4]更新为dp[2][0]

dp[1][5]其他，dp[2][5]更新为dp[2][1]

0 -1 -1 -1 -1 -1 

2 1 0 -1 -1 -1 

1 1 1 -1 0 0 

————–

4

第一个用例：

0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

————–

dp[0][0]不为负,dp[1][0]更新为硬币0的个数。

dp[0][1]其他，dp[1][1]更新为dp[1][0]

dp[0][2]其他，dp[1][2]更新为dp[1][1]

dp[1][2]用完了，dp[1][3]更新为硬币0的个数。

dp[1][3]用完了，dp[1][4]更新为硬币0的个数。

dp[1][4]用完了，dp[1][5]更新为硬币0的个数。

dp[1][5]用完了，dp[1][6]更新为硬币0的个数。

dp[1][6]用完了，dp[1][7]更新为硬币0的个数。

dp[1][7]用完了，dp[1][8]更新为硬币0的个数。

dp[1][8]用完了，dp[1][9]更新为硬币0的个数。

dp[1][9]用完了，dp[1][10]更新为硬币0的个数。

0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

2 1 0 -1 -1 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

————–

dp[1][0]不为负,dp[2][0]更新为硬币1的个数。

dp[1][1]不为负,dp[2][1]更新为硬币1的个数。

dp[1][2]不为负,dp[2][2]更新为硬币1的个数。

dp[1][3]其他，dp[2][3]更新为dp[2][1]

dp[1][4]其他，dp[2][4]更新为dp[2][2]

dp[2][3]用完了，dp[2][5]更新为硬币1的个数。

dp[2][4]用完了，dp[2][6]更新为硬币1的个数。

dp[2][5]用完了，dp[2][7]更新为硬币1的个数。

dp[2][6]用完了，dp[2][8]更新为硬币1的个数。

dp[2][7]用完了，dp[2][9]更新为硬币1的个数。

dp[2][8]用完了，dp[2][10]更新为硬币1的个数。

0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

2 1 0 -1 -1 -1 -1 -1 -1 -1 -1 

1 1 1 0 0 -1 -1 -1 -1 -1 -1 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

————–

dp[2][0]不为负,dp[3][0]更新为硬币2的个数。

dp[2][1]不为负,dp[3][1]更新为硬币2的个数。

dp[2][2]不为负,dp[3][2]更新为硬币2的个数。

dp[2][3]不为负,dp[3][3]更新为硬币2的个数。

dp[2][4]不为负,dp[3][4]更新为硬币2的个数。

dp[2][5]其他，dp[3][5]更新为dp[3][1]

dp[2][6]其他，dp[3][6]更新为dp[3][2]

dp[2][7]其他，dp[3][7]更新为dp[3][3]

dp[2][8]其他，dp[3][8]更新为dp[3][4]

dp[3][5]用完了，dp[3][9]更新为硬币2的个数。

dp[3][6]用完了，dp[3][10]更新为硬币2的个数。

0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 

2 1 0 -1 -1 -1 -1 -1 -1 -1 -1 

1 1 1 0 0 -1 -1 -1 -1 -1 -1 

1 1 1 1 1 0 0 0 0 -1 -1 

————–

8

本以为这次照着书上的思路来的应该没问题了吧，数组再利用就懒得做了。于是提交，结果MLE

于是打起精神来重复利用数组，注意到上图中的箭头都是垂直的，也就是说可以定义

dp[j] := 在第i次循环时之前表示用前i-1种硬币凑成j时第i种硬币最多能剩余多少个（-1表示配不出来），循环之后就表示第i次的状态

于是就省了一维数组：

#include <iostream>
#include <set>
#include <algorithm>
using namespace std;

int dp[100000 + 16]; // dp[i][j] := 用前i种硬币凑成j时第i种硬币最多能剩余多少个
int A[100 + 16];
int C[100 + 16];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n, m;
	while(cin >> n >> m && n > 0)
	{
		memset(dp, -1, sizeof(dp));
		dp[0] = 0;
		for (int i = 0; i < n; ++i)
		{
			cin >> A[i];
		}
		for (int i = 0; i < n; ++i)
		{
			cin >> C[i];
		}
		for (int i = 0; i < n; ++i)
		{
			for (int j = 0; j <= m; ++j)
			{
				if (dp[j] >= 0)
				{
					dp[j] = C[i];
				}
				else if (j < A[i]						// 用一个就超出，不能用
						|| dp[j - A[i]] <= 0)		// 连凑比j小的数的时候都用完了，此时更加用完了
				{
					dp[j] = -1;
				}
				else
				{
					dp[j] = dp[j - A[i]] - 1;		// 用上了一个第i个硬币
				}
			}
		}
		int answer = count_if(dp + 1, dp + 1 + m , bind2nd(greater_equal<int>(), 0)); // 总额0不算在答案内
		cout << answer << endl;
	}
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
    system("out.txt");
#endif
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

提交，AC，并且足足算了2秒钟。这就是男人八题么

12505189 hankcs 1742 Accepted 640K 2032MS C++ 1456B 2014-02-08 20:15:44

知识共享许可协议 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1742 Coins 图表详解 《挑战程序设计竞赛(第2版)》

继续浏览有关 C++ 的文章

评论 3

取消

  • 昵称 (必填)
  • 邮箱 (必填)
  • 网址
  1. #3

    讲的很详细 谢谢了

    Draymonder7年前 (2017-07-27)回复
  2. #2

    博主写的好详细..学习了

    可可豆子cowboy10年前 (2014-07-30)回复
  3. #1

    写的真好! 赞!

    Jecvay10年前 (2014-06-29)回复

我的作品

HanLP自然语言处理包《自然语言处理入门》