
蚂蚁牙黑,蚂蚁牙红:有A只蚂蚁,来自T个家族。同一个家族的蚂蚁长得一样,但是不同家族的蚂蚁牙齿颜色不同。任取n只蚂蚁(S<=n<=B),求能组成几种集合?
这是《2.3 记录结果再利用的“动态规划” 优化递推关系式》练习题的第二题。
定义
dp[i][j] := 使用前i个家族可以配出来“元素个数为j”的集合的个数。
那么dp[0][0] = 1,不使用任何蚂蚁配出空集的个数为1。
递推关系式:
dp[i][j] = ∑0family[i]dp[i – 1][j – k]
前i-1个家族配成j-k的集合们每一个集合都加入k只家族i的蚂蚁,累加得到前i个家族配成j的集合的个数,直观的代码:
#include <iostream>
using namespace std;
#define MOD 1000
int family[1000 + 16]; // 每个家庭有多少只蚂蚁
int dp[1000 + 16][10000 + 16]; // 使用前i个家族可以配出来“元素个数为j”的集合的个数
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int T, A, S, B;
cin >> T >> A >> S >> B;
for (int i = 0; i < A; ++i)
{
int index;
cin >> index;
++family[index];
}
dp[0][0] = 1;
int total = family[0]; // 前i个家族一共有多少只蚂蚁
for (int i = 1; i <= T; ++i)
{
total += family[i];
for (int k = 0; k <= family[i]; ++k)
{
for (int j = total; j >= k; --j)
{
dp[i][j] = (dp[i][j]
+ dp[i - 1][j - k] // 前i-1个家族配成j-k的集合们每一个集合都放入k只
// 家族i的蚂蚁构成新集合,它们必然各不相同
) % MOD;
}
}
}
int result = 0;
for (int i = S; i <= B; ++i)
{
result = (result + dp[T][i]) % MOD;
}
cout << result << endl;
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
由于dp数组每次都是i和i-1,所以可以滚动重复利用:
#include <iostream>
using namespace std;
#define MOD 1000000
int family[1000 + 16]; // 第i个家庭有多少只蚂蚁
int dp[2][100000 + 16]; // 使用前i个家族可以配出来“元素个数为j”的集合的个数
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int T, A, S, B;
cin >> T >> A >> S >> B;
for (int i = 0; i < A; ++i)
{
int index;
cin >> index;
++family[index];
}
dp[0][0] = 1;
int total = 0;
for (int i = 1; i <= T; ++i)
{
total += family[i]; // 前i个家族一共有多少只蚂蚁
int cur = i & 0x1;
int pre = (i - 1) & 0x1;
memset(dp[cur], 0, sizeof(dp[cur]));
for (int k = 0; k <= family[i]; ++k)
{
for (int j = total; j >= k; --j)
{
dp[cur][j] = (dp[cur][j]
+ dp[pre][j - k] // 前i-1个家族配成j-k的集合们每一个集合都放入k只
// 家族i的蚂蚁构成新集合,它们必然各不相同
) % MOD;
}
}
}
int result = 0;
int cur = T & 0x1;
for (int i = S; i <= B; ++i)
{
result = (result + dp[cur][i]) % MOD;
}
cout << result << endl;
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
事实上,这依然不是最优的递推式。在《挑战程序设计竞赛(第2版)》P69给出了一个更加优化的递推式,将
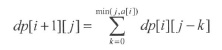
优化为
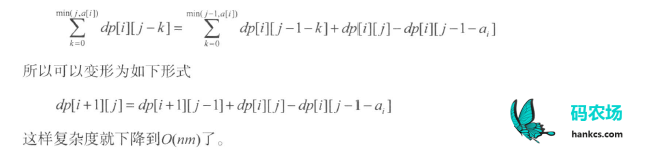
比较优化前后的项数变化,发现![]() 比
比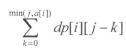 少了一项dp[i][j],多了一项dp[i][j-1-ai],于是分别加上少的项,减去多的项就得到上面的优化递推式。
少了一项dp[i][j],多了一项dp[i][j-1-ai],于是分别加上少的项,减去多的项就得到上面的优化递推式。
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3046 Ant Counting 题解 《挑战程序设计竞赛(第2版)》
知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3046 Ant Counting 题解 《挑战程序设计竞赛(第2版)》
 码农场
码农场
请问为什么不能优化为一维数组?pre和cur是什么意思?