《算法导论》果然是本神一般的书，偏向理论，大而全，大量公式与推导让人眩晕。我发现光看不思考没多大效果，于是也写点笔记，整理一下别人绘制的图解，效果可能好一些。

第一部分 基础知识 

强调了算法的重要性，号召大家都来买书研究算法。介绍了一些常见的数学符号，以及最基本的递归和算法复杂度分析。

第五章 概率分析和随机算法完全是为了第二部分 排序和顺序统计学做铺垫的。其中提出的生日悖论很有意思，求解一个房间里至少有多少人才能保证随机抽取两人此两人生日相同概率>0.5。

解法是求逆事件，k个人生日不同的概率。

1个人生日不同的概率是1

两个人生日不同的概率是1 * 364 / 365

三个人生日不同的概率是1 * 364 / 365 * 363 / 365

……

k个人生日不同的概率是1 * 364 / 365 * 363 / 365 …… (366 – k) / 365

接着《算法导论》用了一个很冷艳的不等式1 + x ≤ 1 + e^x 放大了上式，解出了结果。

但是我考虑到k肯定是1 ~ 365 中间的某个数，解空间固定的话直接穷举不就得了。最后的结果小得惊人，23个人。

第二部分 排序和顺序统计学

讲解了堆排序，快速排序，计数排序，基数排序，桶排序。第九章中位数我感觉应用的话，应该用在基数排序的“中轴”的选取上。

其中没讲到的冒泡、插入、选择排序属于第一部分 基础知识的内容。

这里用图解做个记录，图解转自http://www.cppblog.com/guogangj/archive/2009/11/13/100876.html

冒泡排序

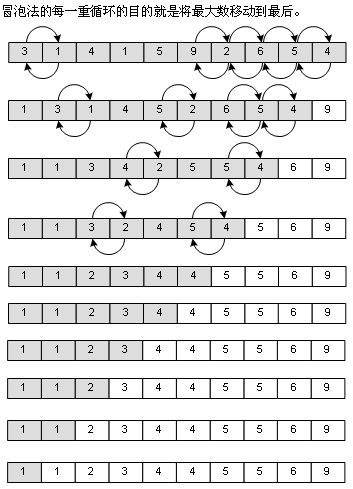
直接插入排序

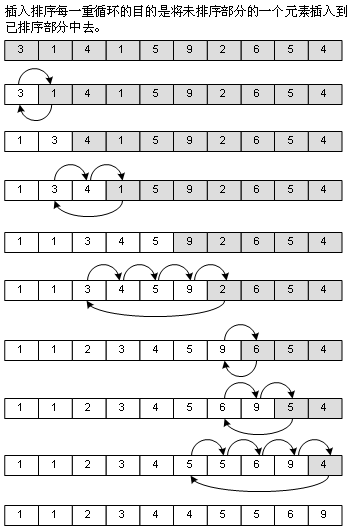
直接选择排序

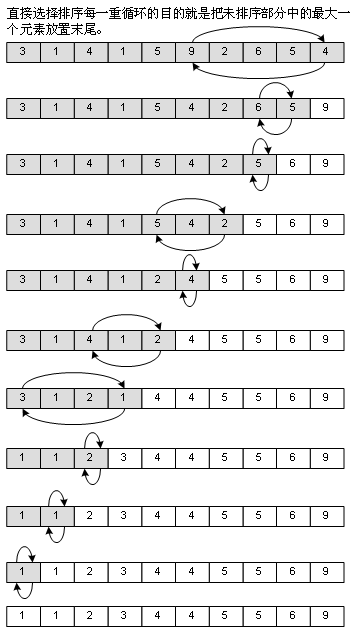
快速排序

图解来自http://www.cnblogs.com/morewindows/archive/2011/08/13/2137415.html ，这是我见过最通俗的讲解

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

该方法的基本思想是：

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

 

虽然快速排序称为分治法，但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明：挖坑填数+分治法：

先来看实例吧，定义下面再给出（最好能用自己的话来总结定义，这样对实现代码会有帮助）。

 

以一个数组作为示例，取区间第一个数为基准数。

0	1	2	3	4	5	6	7	8	9
72	6	57	88	60	42	83	73	48	85

初始时，i = 0;  j = 9;   X = a[i] = 72

由于已经将a[0]中的数保存到X中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。

从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++;  这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j–;

 

数组变为：

0	1	2	3	4	5	6	7	8	9
48	6	57	88	60	42	83	73	88	85

 i = 3;   j = 7;   X=72

再重复上面的步骤，先从后向前找，再从前向后找。

从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;

从i开始向后找，当i=5时，由于i==j退出。

此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

 

数组变为：

0	1	2	3	4	5	6	7	8	9
48	6	57	42	60	72	83	73	88	85

可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。

计数排序

核心思想是对每个元素，统计比它小的元素的个数。为此先开一个数组C，C的下标是元素值，值是元素出现次数，再开一个数组B存放结果。

基数排序

先按照低位排序，再按照高位排序

桶排序

其实跟计数排序一个道理，不过是针对元素∈[0 ,1)且均匀分布特化的一个算法。

性能分析表：

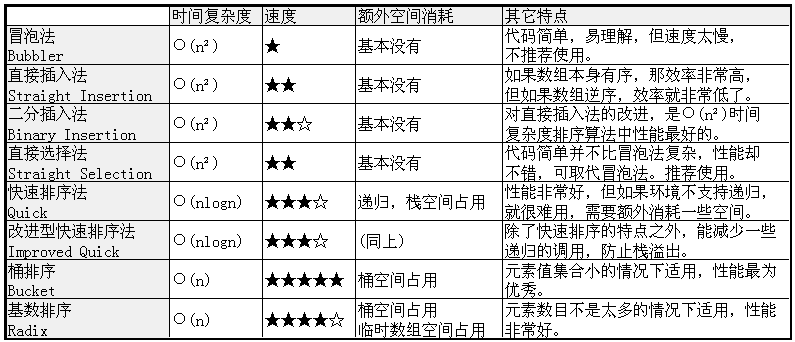
 知识共享署名-非商业性使用-相同方式共享：码农场 » 白话图解《算法导论》第一二部分