目录
这是LaTex答案,Python代码开源在GitHub上。先进行大量的SG、CBOW、负采样、交叉熵损失函数推导和证明,理论基础扎实后平滑过渡到实现;在斯坦福情感树库上做情感分析、调参、分析混淆矩阵与错误。
以前看不懂公式,总觉得代码是最重要的;现在觉得代码无关紧要了。
另需注意,公式中的向量是列向量,而代码中的向量是行向量(效率更高)。
1:Softmax
a softmax常数不变性
证明softmax不受输入的常数偏移影响,即
$$softmax(x) = softmax(x + c)$$
解答:
$$\require{cancel}
\begin{align} (softmax(x + c))_{i} &= \frac{e^{x_{i} + c}}{\sum_{j} e^{x_{j} + c}} %
= \frac{e^{x_{i}} \times e^{c}}{e^{c} \times \sum_{j} e^{x_{j}}} \nonumber \\
%
&= \frac{e^{x_{i}} \times \cancel{e^{c}}}{\cancel{e^{c}} \times \sum_{j} e^{x_{j}}} %
= (softmax(x))_{i} \nonumber
\end{align}$$
b Python实现
利用上述的公式实现优化版的softmax,要求既能处理向量,也能处理矩阵(视作多个不相干的行向量集合)。
def softmax(x): """Compute the softmax function for each row of the input x. It is crucial that this function is optimized for speed because it will be used frequently in later code. You might find numpy functions np.exp, np.sum, np.reshape, np.max, and numpy broadcasting useful for this task. Numpy broadcasting documentation: http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html You should also make sure that your code works for a single N-dimensional vector (treat the vector as a single row) and for M x N matrices. This may be useful for testing later. Also, make sure that the dimensions of the output match the input. You must implement the optimization in problem 1(a) of the written assignment! Arguments: x -- A N dimensional vector or M x N dimensional numpy matrix. Return: x -- You are allowed to modify x in-place """ orig_shape = x.shape if len(x.shape) > 1: # Matrix ### YOUR CODE HERE exp_minmax = lambda x: np.exp(x - np.max(x)) denom = lambda x: 1.0 / np.sum(x) x = np.apply_along_axis(exp_minmax, 1, x) denominator = np.apply_along_axis(denom, 1, x) if len(denominator.shape) == 1: denominator = denominator.reshape((denominator.shape[0], 1)) x = x * denominator ### END YOUR CODE else: # Vector ### YOUR CODE HERE x_max = np.max(x) x = x - x_max numerator = np.exp(x) denominator = 1.0 / np.sum(numerator) x = numerator.dot(denominator) ### END YOUR CODE assert x.shape == orig_shape return x
为什么要费力气减掉一个最大值常量呢?参考:《计算指数函数的和的对数》。
2:神经网络基础
a sigmoid梯度
很简单的推导:
$$\begin{align}
\sigma(x) &= \frac{1}{1 + e^{-x}} \nonumber \\
%
&= \frac{e^{x}}{1 + e^{x}} \nonumber \\
%
\frac{\partial}{\partial x} \sigma(x) &= \frac{e^{x} \times (1 + e^{x}) – (e^{x} \times e^{x})}{(1 + e^{x})^{2}} \nonumber \\
%
&= \frac{e^{x} + \cancel{(e^{x} \times e^{x})} – \cancel{(e^{x} \times e^{x})}}{(1 + e^{x})^{2}} \nonumber \\
%
&= \frac{e^{x}}{1 + e^{x}} \times \frac{1}{1 + e^{+x}} \nonumber \\
&= \sigma(x) \times \sigma(-x) \nonumber \\
&= \sigma(x) \times (1 – \sigma(x)) \nonumber \\
\end{align}$$
b 交叉熵损失函数的梯度
请推导交叉熵损失函数关于softmax输入 $\boldsymbol{\theta}$ 的梯度,记假设函数为
$$\hat{\mathbf{y}}=softmax(\boldsymbol{\theta})$$
交叉熵损失函数为:
$$\begin{equation}
CE(\mathbf{y},\hat{\mathbf{y}}) = – \sum_{i} y_{i} \times log(\hat{y_{i}})
\end{equation}$$
其中$\mathbf{y}$是one-hot向量,$\hat{\mathbf{y}}$是概率向量。
解答:
记$S$为softmax函数,引入下列记号:
$$\begin{align}
f_{i} &= e^{\theta_{i}} \nonumber \\
%
g_{i} &= \sum_{k=1}^{K} e^{\theta_{k}} \nonumber \\
%
S_{i} &= \frac{f_{i}}{g_{i}} \nonumber \\
%
\frac{\partial S_{i}}{\partial \theta_{j}} &= \frac{f'_{i} g_{i} – g'_{i} f_{i}}{g_{i}^{2}} \nonumber
\end{align}$$
这里的下标表示取标量分别求导,当$i = j$时:
$$\begin{align}
f'_{i} &= f_{i};g'_{i} = e^{\theta_{j}} \nonumber \\
\frac{\partial S_{i}}{\partial \theta_{j}} &= \frac{e^{\theta_{i}} \sum_{k} e^{\theta_{k}} – e^{\theta_{j}} e^{\theta_{i}} }{ (\sum_{k} e^{\theta_{k}})^{2} } \nonumber \\
&= \frac{e^{\theta_{i}}}{\sum_{k} e^{\theta_{k}}} \times \frac{\sum_{k} e^{\theta_{k}} – e^{\theta_{j}}}{\sum_{k} e^{\theta_{k}}} \nonumber \\
&= S_{i} \times (1 – S_{i}) \nonumber
\end{align}$$
当$i \ne j$时:
$$\begin{align}
f'_{i} &= 0;g'_{i} = e^{\theta_{j}} \nonumber \\
\frac{\partial S_{i}}{\partial \theta_{j}} %
&= \frac{0 – e^{\theta_{j}} e^{\theta_{i}}}{(\sum_{k} e^{\theta_{k}})^{2}} \nonumber \\
%
&= – \frac{e^{\theta_{j}}}{\sum_{k} e^{\theta_{k}}} \times \frac{e^{\theta_{i}}}{\sum_{k} e^{\theta_{k}}} \nonumber \\
%
&= -S_{j} \times S_{i} \nonumber
\end{align}$$
接下来正式推导:
$$\begin{align}
\frac{\partial CE}{\partial \theta_{i}} %
&= – \sum_{k} y_{k} \frac{\partial log S_{k}}{\partial \theta_{i}} \nonumber \\
%
&= – \sum_{k} y_{k} \frac{1}{S_{k}} \frac{\partial S_{k}}{\partial \theta_{i}} \nonumber \\
%
&= – y_{i} (1 – S_{i}) – \sum_{k \ne i} y_{k} \frac{1}{S_{k}} (-S_{k} \times S_{i}) \nonumber \\
%
&= – y_{i} (1 – S_{i}) + \sum_{k \ne i} y_{k} S_{i} \nonumber \\
%
&= – y_{i} + y_{i} S_{i} + \sum_{k \ne i} y_{k} S_{i} \nonumber \\
%
&= S_{i}(\sum_{k} y_{k}) – y_{i} \nonumber
\end{align}$$
由于概率归一化$\sum_{k} y_{k} = 1$:
$$\begin{align}
\frac{\partial CE}{\partial \theta_{i}} %
&= S_{i} – y_{i} \nonumber
\end{align}$$
c 推导三层网络的梯度
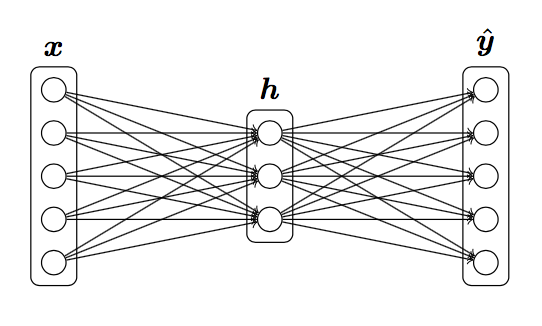
损失函数$J = CE(\mathbf{y}, \hat{\mathbf{y}})$,求 $\frac{\partial J}{\partial \boldsymbol{x}}$,可使用的符号有:
$$\begin{align}
\mathbf{h} &= sigmoid(\boldsymbol{xW}_{1} + \boldsymbol{b}_{1}) \\
\hat{\boldsymbol{y}} &= softmax(\boldsymbol{hW}_{2} + \boldsymbol{b}_{2}) \nonumber
\end{align}$$
记$z_{2} = \boldsymbol{xW}_{1} + \boldsymbol{b}_{1}$ , $z_{3} = \boldsymbol{hW}_{2} + \boldsymbol{b}_{2}$;
$$\begin{align} \frac{\partial CE}{\partial z_{3}} &= \boldsymbol{\delta}_{3} = \hat{\boldsymbol{y}} – \boldsymbol{y} \nonumber \\ \frac{\partial CE}{\partial \boldsymbol{h}} &= \boldsymbol{\delta}_{2} = \boldsymbol{\delta}_{3}\boldsymbol{W}_{2}^{T} \nonumber \\ \frac{\partial CE}{\partial z_{2}} &= \boldsymbol{\delta}_{1} = \boldsymbol{\delta}_{2} \circ \sigma'(z_{2}) \nonumber \\ \frac{\partial CE}{\partial \boldsymbol{x}} &= \boldsymbol{\delta}_{1} \frac{\partial z_{2}}{\partial \boldsymbol{x}} \nonumber \\ &= \boldsymbol{\delta}_{1} \boldsymbol{W}_{1}^{T} \nonumber \end{align}$$
d 参数数量
对于上述神经网络,一共有多少个参数。假设输入维度是$D_{x}$,隐藏单元数为$H$,输出维度为$D_{y}$。
解答:
$$\begin{align}
n_{W_{1}} &= D_{x} \times H \nonumber \\
%
n_{b_{1}} &= H \nonumber \\
%
n_{W_{2}} &= H \times D_{y} \nonumber \\
%
n_{b_{2}} &= D_{y} \nonumber \\
%
N &= (D_{x} \times H) + H + (H \times D_{y}) + D_{y} \nonumber\\
&=(D_x+1)\times H+(H+1)\times D_y
\end{align}$$
e 实现sigmoid函数
太简单了:
def sigmoid(x): """ Compute the sigmoid function for the input here. Arguments: x -- A scalar or numpy array. Return: s -- sigmoid(x) """ ### YOUR CODE HERE s = 1.0 / (1 + np.exp(-x)) ### END YOUR CODE return s def sigmoid_grad(s): """ Compute the gradient for the sigmoid function here. Note that for this implementation, the input s should be the sigmoid function value of your original input x. Arguments: s -- A scalar or numpy array. Return: ds -- Your computed gradient. """ ### YOUR CODE HERE ds = s * (1 - s) ### END YOUR CODE return ds
f 实现梯度检查
关于梯度检查的原理参考CS229:http://www.hankcs.com/ml/neural-networks-learning-cs229.html#h3-7
实现如下:
def gradcheck_naive(f, x): """ Gradient check for a function f. Arguments: f -- a function that takes a single argument and outputs the cost and its gradients x -- the point (numpy array) to check the gradient at """ rndstate = random.getstate() random.setstate(rndstate) fx, grad = f(x) # Evaluate function value at original point h = 1e-4 # Do not change this! # Iterate over all indexes in x it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) while not it.finished: ix = it.multi_index # Try modifying x[ix] with h defined above to compute # numerical gradients. Make sure you call random.setstate(rndstate) # before calling f(x) each time. This will make it possible # to test cost functions with built in randomness later. ### YOUR CODE HERE: x[ix] += h random.setstate(rndstate) new_f1 = f(x)[0] x[ix] -= 2*h random.setstate(rndstate) new_f2 = f(x)[0] x[ix] += h numgrad = (new_f1 - new_f2) / (2 * h) ### END YOUR CODE # Compare gradients reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix])) if reldiff > 1e-5: print "Gradient check failed." print "First gradient error found at index %s" % str(ix) print "Your gradient: %f \t Numerical gradient: %f" % ( grad[ix], numgrad) return it.iternext() # Step to next dimension print "Gradient check passed!"
g 实现前向传播和反向传播
def forward_backward_prop(data, labels, params, dimensions): """ Forward and backward propagation for a two-layer sigmoidal network Compute the forward propagation and for the cross entropy cost, and backward propagation for the gradients for all parameters. Arguments: data -- M x Dx matrix, where each row is a training example. labels -- M x Dy matrix, where each row is a one-hot vector. params -- Model parameters, these are unpacked for you. dimensions -- A tuple of input dimension, number of hidden units and output dimension """ ### Unpack network parameters (do not modify) ofs = 0 Dx, H, Dy = (dimensions[0], dimensions[1], dimensions[2]) W1 = np.reshape(params[ofs:ofs+ Dx * H], (Dx, H)) ofs += Dx * H b1 = np.reshape(params[ofs:ofs + H], (1, H)) ofs += H W2 = np.reshape(params[ofs:ofs + H * Dy], (H, Dy)) ofs += H * Dy b2 = np.reshape(params[ofs:ofs + Dy], (1, Dy)) ### YOUR CODE HERE: forward propagation h = sigmoid(np.dot(data,W1) + b1) yhat = softmax(np.dot(h,W2) + b2) ### END YOUR CODE ### YOUR CODE HERE: backward propagation cost = np.sum(-np.log(yhat[labels==1])) / data.shape[0] d3 = (yhat - labels) / data.shape[0] gradW2 = np.dot(h.T, d3) gradb2 = np.sum(d3,0,keepdims=True) dh = np.dot(d3,W2.T) grad_h = sigmoid_grad(h) * dh gradW1 = np.dot(data.T,grad_h) gradb1 = np.sum(grad_h,0) ### END YOUR CODE ### Stack gradients (do not modify) grad = np.concatenate((gradW1.flatten(), gradb1.flatten(), gradW2.flatten(), gradb2.flatten())) return cost, grad
 码农场
码农场
直接运行q3_run的话,得到的word_vector是保存在哪里? 运行了好像没找到输出文件啊
“负采样时的梯度推导” 对Vc求导中。里面的log怎么不见了?
请忽略这个问题。。。。
(1)gradcheck_naive函数中,numgrad = (new_f1 – new_f2) / (2 * h)这一行不应该是numgrad = (new_f1 – new_f2) / (2 * h)[ix]吗,然后后面才和grad[ix]比较呀?
(2)gradcheck_naive函数中31行,被除的分母max(1, abs(numgrad), abs(grad[ix]))啥意思?为啥不是直接拿误差和1e-5比较?
新手求解答,谢谢
应该是numgrad = ((new_f1 – new_f2) / (2 * h))[ix]
请问有人知道这个问题的吗?能不能解释一下,谢谢!
我认为3.a的原答案是对的,y_hat(算出每个词的概率)和y应该是W*1维,U是D*W维,那么U(y_hat – y)是对得上的。
感谢指正。
请问2.g里line 33 grad_h = sigmoid_grad(h) * dh, 为什么是求的sigmoid_grad(h)?
假设定义z=np.dot(data,W1) + b1,那么h = sigmoid(z),使用链式法则推导的时候有partial_h/partial_z = sigmoid(z)不是吗?
博主你好,请问2g部分里gradb2和gradb1是用什么公式求的?
The bias gradients for neuron $i$ on layer $k$ is simply $\delta^{(k)}_i$. And $\sum$ is for the average loss on whole batch.
negSamplingCostAndGradient 里面是不是有些问题之 indices你都没有使用到,而且采用的dataset.getSample 没有考虑到重复target word 的问题, 后面在计算器smalpe word的cost的时候 和assignment上面计算的公式有出入
$$
\begin{align} \sigma(x) &= \frac{1}{1 + e^{-x}} \\
\sigma(-x) &= \frac{1}{1 + e^{x}} \\
&=\frac{e^{-x}}{1 + e^{-x}}\\
&=1-\sigma(x)
\end{align}
$$
您好博主,请问2g部分29行 为什么yhat-labels之后还要除以data.shape[0],反向传播求出来的不就是直接yhat-y吗。除以data.shape[0]的作用是什么?
我来试着回答一下,这是因为28行的cost函数用的是average cross entropy,即除以data.shape[0]求平均,所以求导也会带着它,并不影响反向传播
可是代码要求部分,说的是Note: compute cost based on `sum` not `mean`.诶
我智障了,y是D×1维
说错了。。y的维数是W×1(有W个词),U的维数是D×W,U(y_hat – y)维数对的上
3.a 答案是对的吧,y的维数是D*1,U^T的维数是W×D,没有问题哇
3e部分的负采样与梯度,为什么不用源代码已经抽取的下标?为什么重新抽取下标?
太谢谢您了~!!
从课程官网下载的 assignment1.zip 中的 get_datasets.sh 脚本里面的数据集获取地址好像已经失效了,不知道博主的更新过的脚本是从哪里下载的?
你好,碰巧是跟你一个情况,昨天我也弄了好久。
博主提供的百度云网盘里有assignment1/u…/dataset这个文件夹。应该是下载了,拷贝过去就行。
兄弟,百度云盘的地址在哪? 没看见,只看到了github的地址。 我也发现那个sh文件的链接失效了–
博主关于cs224n发的第一个博文
glove那个数据集链接确实失效了,谷歌搜索一下`stanford glove`就能找到了
a部分中,yhat是D x 1, U是W x D才对
predicted是Dx1, target是Dx1, outputVectors是WxD, yhat是Wx1。这回没错了
我的理解是,$\boldsymbol{U} = [\boldsymbol{u}_{1}$,$\boldsymbol{u}_{1}$,$\dots$, $\boldsymbol{u}_{W}]$中的逗号应该表示按列拼接的意思,所以是$D \times W$。逗号和分号的意思不同,matlab中[1,2,3]是行向量,[1;2;3]才是列向量。
一个u表示一条单词的向量表示,Python中不以分号作为分隔,而且outputVector数量应是W个,向量维度是D
另外,在讲义中出现过$u_{c}^{T}\hat{v}$,所以$u$和$v$的维度应该都是一样的$D \times 1$
我也这么认为,看了前面neural network的那道题目中,weights维度的定义一般都是Dim(in) * Dim(out)的,然后outputVectors我输出了一下它的shape也是W*d,所以感觉博主这里的维度定义的不一样。
博主,3.a部分的为什么不是$z=U^\mathrm{T} \cdot v_c$,U的shape是D*W, $v_c$的shape是D*1。
你是对的