计算指数函数的和的对数-码农场

证明
实现
Reference

译自哈佛大学《Computing Log-Sum-Exp》。在许多ML库中，经常看到这类函数，如scipy中的misc.logsumexp、CRF++中的CRFPP::logsumexp，其意义何在？

这篇文章旨在讲解这个必学，却没有任何ML课程会特意教的技巧。假设我们有N个实数，我们想求下式：

quicklatex (1).png

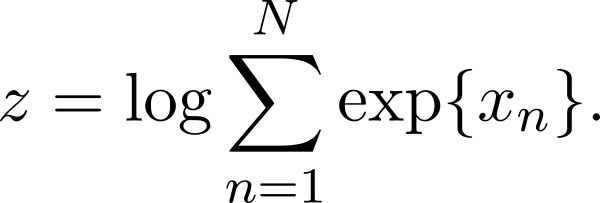
这是非常常见的需求，比如你想用softmax去计算一个多项式分布（多分类逻辑回归）。你要计算对数似然的话，你就得计算上式这种规范化因子。如果很大或很小，朴素的直接计算会上溢出或下溢出，从而导致严重问题。举个例子，对于，直接计算是可行的，我们可以得到1.55。但对于，却并不可行，我们会得到；对于，还是不行，我们会得到。这是怎么回事？很简单，你的浮点数只有64位，在计算指数函数的环节，，会发生上溢出；，会发生下溢出。即便在数学世界上式的值显然不是无穷大，但在计算机的浮点数世界里就是求不出来。怎么办呢？

解决方案很简单：

quicklatex (13).png

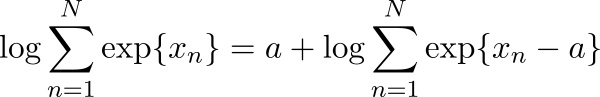
对任意a都成立，这意味着我们可以自由地调节指数函数的指数部分，一个典型的做法是取中的最大值：

这可以保证指数最大不会超过0，于是你就不会上溢出。即便剩余的部分下溢出了，你也能得到一个合理的值。

证明

屏幕快照 2016-08-13 下午9.23.38.png

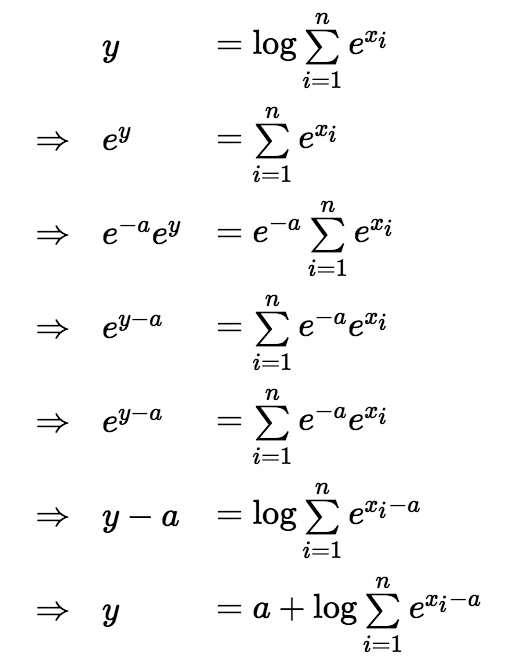
实现

CRF++中的实现如下：

#define MINUS_LOG_EPSILON  50
// log(exp(x) + exp(y));
//    this can be used recursivly
// e.g., log(exp(log(exp(x) + exp(y))) + exp(z)) =
// log(exp (x) + exp(y) + exp(z))
inline double logsumexp(double x, double y, bool flg)
{
    if (flg)
        return y;  // init mode
    const double vmin = std::min(x, y);
    const double vmax = std::max(x, y);
    if (vmax > vmin + MINUS_LOG_EPSILON)
    {
        return vmax;
    }
    else
    {
        return vmax + std::log(std::exp(vmin - vmax) + 1.0);
    }
}