Chang et al. 2015提出加速结构化学习的近似算法AI-DCD,通过缓存整数线性规划中相似的问题及解,减少对ILP solver的调用次数,从而加速训练,同时不损失精度。
平摊推断
记$\mathbf{y}=\{y_1,y_2,\cdots y_N\}$为一个结构,其中$y_j \in \mathcal{Y}_j$是输出变量$y_j$的所有可选离散值(比如序列标注中的某个元素的标签预测);$\mathbf{y} \in \mathcal{Y}$是所有可能的结构(比如所有可能的标注序列)。则结构化预测中的学习问题就是在给定模型$\mathbf{w}$的情况下,找出最佳的结构
$$\begin{equation}
y^{*}=\arg \max_{\mathbf{y} \in \mathcal{Y}} \mathbf{w}^T \phi(\mathbf{x},\mathbf{y})
\end{equation}$$
其中,$\phi(\mathbf{x},\mathbf{y})$是根据$\mathbf{x}$和$\mathbf{y}$提取出来的特征向量。
输出$\mathbf{y}$还可以被表示为二进制向量$\mathbf{z}=\{z_{j,a}\vert j=1 \cdots N, a \in \mathcal{Y}_j \}$,$\mathbf{z}\in \mathcal{Z} \subset \{0,1\}^{\sum |\mathcal{Y}_i|}$,其中$z_{j,a}$表示中间步骤$y_j$是否是产生最终结构$\mathbf{y}_a$的一环。
如此,式(1)可被重写为受约束的二值线性规划(ILP):
$$\begin{equation}
\mathbf{z}^{*}=\arg \max_{\mathbf{z}\in \mathcal{Z}} \mathbf{c}^T\mathbf{z}
\end{equation}$$
其中$\mathbf{c}^T\mathbf{z} = \mathbf{w}^T \phi(\mathbf{x}_i,\mathbf{y})$,约束是$\sum _a z_{j,a}=1$,记$c_{j,a}$为$z_{j,a}$的系数。既然$\mathbf{z}$是二值向量,也就是说,约束每个中间结果只导向一个结构的产生。比如词性标注中单词只能有一个词性,再比如联合实体关系抽取任务是这样被形式化为ILP问题的:
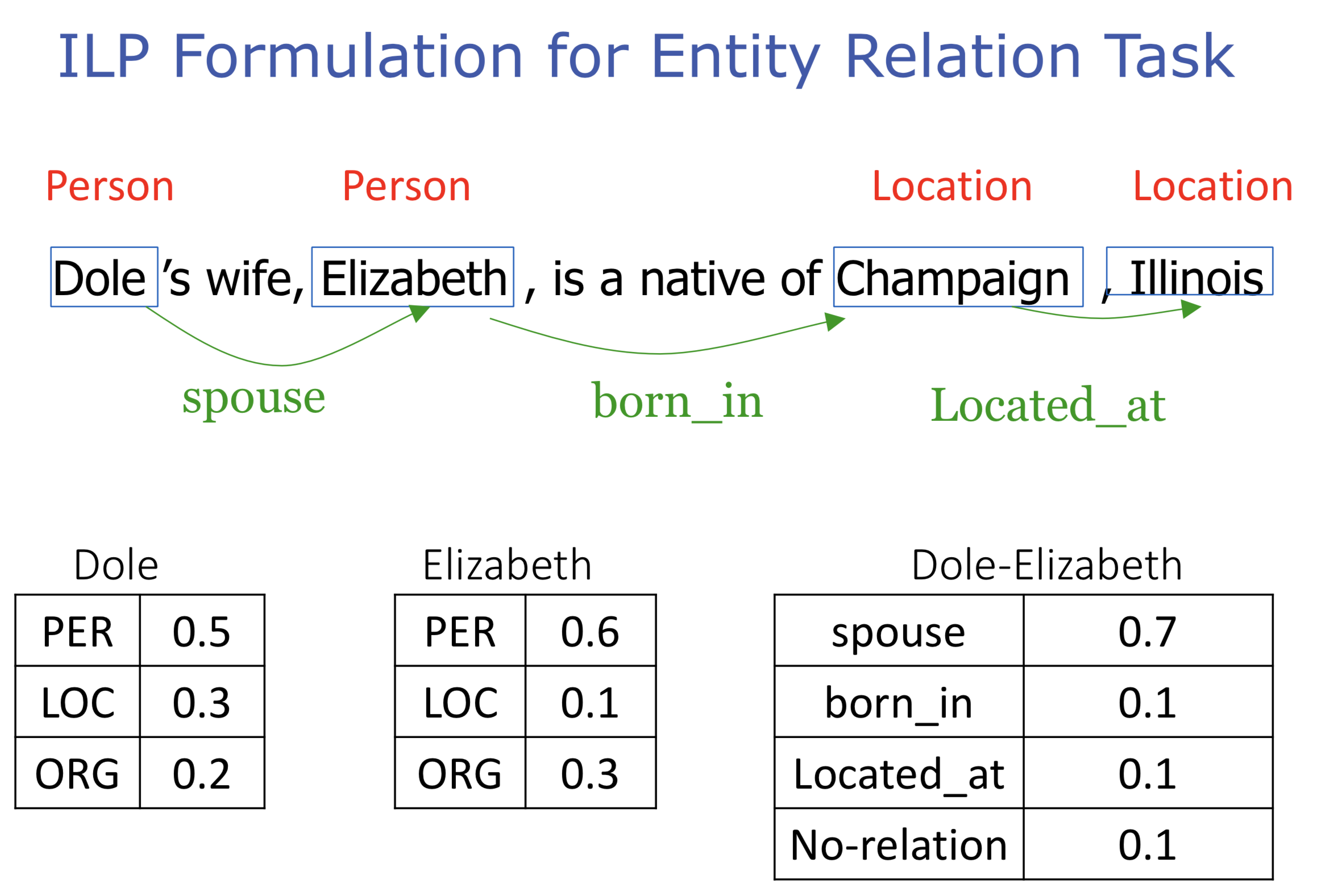
每个词语是实体的概率如表格所示,ILP的转化方法为:

这里的$y$都是二值向量中的元素,对应于论文中的$z$。最后一个式子是约束配偶关系只能成立于两个人名之上。
一些特殊的结构(如标注序列)允许将推断问题转化为搜索问题,然后通过高效精确的算法(如维特比算法)解决。而其他场景下的推断问题则是计算代价昂贵的,所以希望得到缓解。
Srikumar, Kundu, and Roth 2012发现(1)不同的目标函数常常导致相同的解,(2)哪怕所有可能的结构是指数级,实际上成立的只有少数。他们通过刻画那些共享式(2)中相同解的问题来加速推断。
他们提出了下列理论:
理论1 定义$\mathbf{p}$和$\mathbf{q}$为两个拥有相同解空间和变量数目(比如等长的标注序列)的推断问题。记$\mathbf{y}^{\mathbf{p}}=\{y_1^{\mathbf{p}},y_2^{\mathbf{p}},\cdots y_N^{\mathbf{p}}\}$和$\mathbf{y}^{\mathbf{q}}=\{y_1^{\mathbf{q}},y_2^{\mathbf{q}},\cdots y_N^{\mathbf{q}}\}$为两者的最优解,同理有$\mathbf{z}^{p}$和$\mathbf{z}^{q}$。记两者的目标函数分别为$f^{\mathbf{p}}(\mathbf{z})=\mathbf{c}^\mathbf{p} \cdot \mathbf{z}$和$f^{\mathbf{q}}(\mathbf{z})=\mathbf{c}^\mathbf{q} \cdot \mathbf{z}$。假设$f^{\mathbf{p}}(\mathbf{z}) \geq0$和$f^{\mathbf{q}}(\mathbf{z}) \geq0$,如果存在常数$M\in \mathcal{R}^+$使得:
$$\begin{equation}
M \geq \sum_j\left(|c_{j,y_j^\mathbf{p}}^\mathbf{p}|+|c_{j,y_j^\mathbf{q}}^\mathbf{p}|\right)/f^{\mathbf{q}}(\mathbf{z}^\mathbf{p})
\end{equation}$$
并且$\mathbf{c}^\mathbf{p}$和$\mathbf{c}^\mathbf{q}$满足下列条件:
$$\begin{equation}
(2z^\mathbf{p}_{j,a}-1)(c_{j,a}^\mathbf{p}-c_{j,a}^\mathbf{q})\leq \epsilon|c^{\mathbf{q}}_{j,a}|,\qquad \forall j,a
\end{equation}$$
则称$\mathbf{z}^{\mathbf{p}}$是$\mathbf{q}$的$(1/(1+M\epsilon))-$近似,也就是说有结论$f^{\mathbf{q}}(\mathbf{z}^\mathbf{q})\leq(1+M\epsilon)f^\mathbf{q}(\mathbf{z}^\mathbf{p})$。
为了利用这个理论,只要缓存$(\mathbf{p},\mathbf{c}^\mathbf{p})$以及$\mathbf{y}^\mathbf{p}$;下次遇到一个新问题$\mathbf{q}$,只要找到缓存中满足式(4)的$\mathbf{p}$,就能得到“$\mathbf{q}$的解是$\mathbf{y}^\mathbf{p}$”的分数的$(1/(1+M\epsilon))-$上界,如此可以省去一次推断过程。
这里的$\epsilon$是一个tolerance超参数,取$0$时上述解是精确的;该值越大,可平摊的推断问题越多,但得到非最优解的风险就越大。
利用Amortized Inference加速训练
以前的研究大多将推断过程当成黑盒子,作者提出应当结合具体模型设计算法:用于结构化SVM的AI-DCD(Amortized Inference framework for Dual Coordinate Descent)和用于结构化感知机的AI- SP(Amortized Inference for Structured Perceptron)。
加速结构化SVM
给定标注训练集$\{\mathbf{x}_i,\mathbf{y}_i\}^l_{i=1}$,$\mathbf{x}_i\in \mathcal{X}$,$\mathbf{y}_i\in\mathcal{Y}$,其中$l$代表实例$i$的长度。结构化SVM最优化问题的原始形式是:
$$\begin{equation}
\min_{\omega,\xi}\;\frac{1}{2}\omega^T\omega+C\sum_i\mathcal{l}(\xi_i)\\
s.t.\; \omega^T\phi(\mathbf{y},\mathbf{y}_i,\mathbf{x}_i)\geq\Delta (\mathbf{y}_i,\mathbf{y})-\xi_i,\; \forall_i,\mathbf{y}\in \mathcal{Y}
\end{equation}$$
其中$\omega^T\phi(\mathbf{y},\mathbf{y}_i,\mathbf{x}_i)=\phi(\mathbf{y}_i,\mathbf{x}_i)-\phi(\mathbf{y},\mathbf{x}_i)$,$\mathbf{y}_i$是gold structure、$\mathbf{y}$是预测结果,$\Delta (\mathbf{y}_i,\mathbf{y})$是衡量两者差别的损失函数,$\mathcal{l}(\xi)=\xi^2$是L2正则。DCD解决原始问题(5)的对偶形式:
$$\begin{align}
\min_{\alpha\geq0}\;&\frac{1}{2} \left\Vert\sum_{\alpha_{i,\mathbf{y}}}\alpha_{i,\mathbf{y}}\phi (\mathbf{y},\mathbf{y}_i,\mathbf{x}_i)\right\Vert^2\\ \notag
&+\frac{1}{4C}\sum_i\left(\sum_\mathbf{y}\alpha_{i,\mathbf{y}}\right)^2-\sum_{i,\mathbf{y}}\Delta\left(\mathbf{y},\mathbf{y}_i\right)\alpha_{i,\mathbf{y}}
\end{align}$$
记式(6)为损失函数$D(\alpha)$,其中的参数非常多,对偶方法只维护并更新一个子集中的$\alpha_{i,\mathbf{y}} \in \mathcal{A}$。作者在另一篇论文中提出的dual coordinate descent (DCD) (Chang and Yih 2013)对待更新的拉格朗日乘子的选择方法是,对每个样本$\mathbf{x}_i$找到最大的:
$$\begin{align}
\bar{\mathbf{y}}&=\arg \max_{\mathbf{y} \in \mathcal{Y}} \; \left( -\nabla D(\mathbf{\alpha})\right)_{i,\mathbf{y}} \\
&=\arg \max_{\mathbf{y} \in \mathcal{Y}} \; \mathbf{\omega}^T\phi(\mathbf{x}_i,\mathbf{y})+\Delta(\mathbf{y}_i,\mathbf{y})\notag
\end{align}$$
然后将满足下列条件的$\alpha_{i,\mathbf{\bar{y}}}$加入$\mathcal{A}$:
$$\begin{align}
-\nabla D( \mathbf { \alpha })_{i,\mathbf{\bar{y}}}>\delta,
\end{align}$$
其中$\delta$是个超参数。
于是在训练过程中遍历样本,执行推断——求解式(7)所定义的ILP;然后缓存满足式(8)的$\alpha_{i,\mathbf{\bar{y}}}$的$(\mathbf{\bar{y}},\mathbf{q})$。在推断的过程中,满足条件(4)的时候直接返回缓存中的$\mathbf{y_q}$。推断算法框架如下:

参数更新、停止条件等细节与平摊推断关系不大,略过。
加速结构化感知机
同为在线学习算法,可应用类似的缓存技巧。
试验
在实体关系抽取任务上应用平摊推断技巧到结构化SVM上:
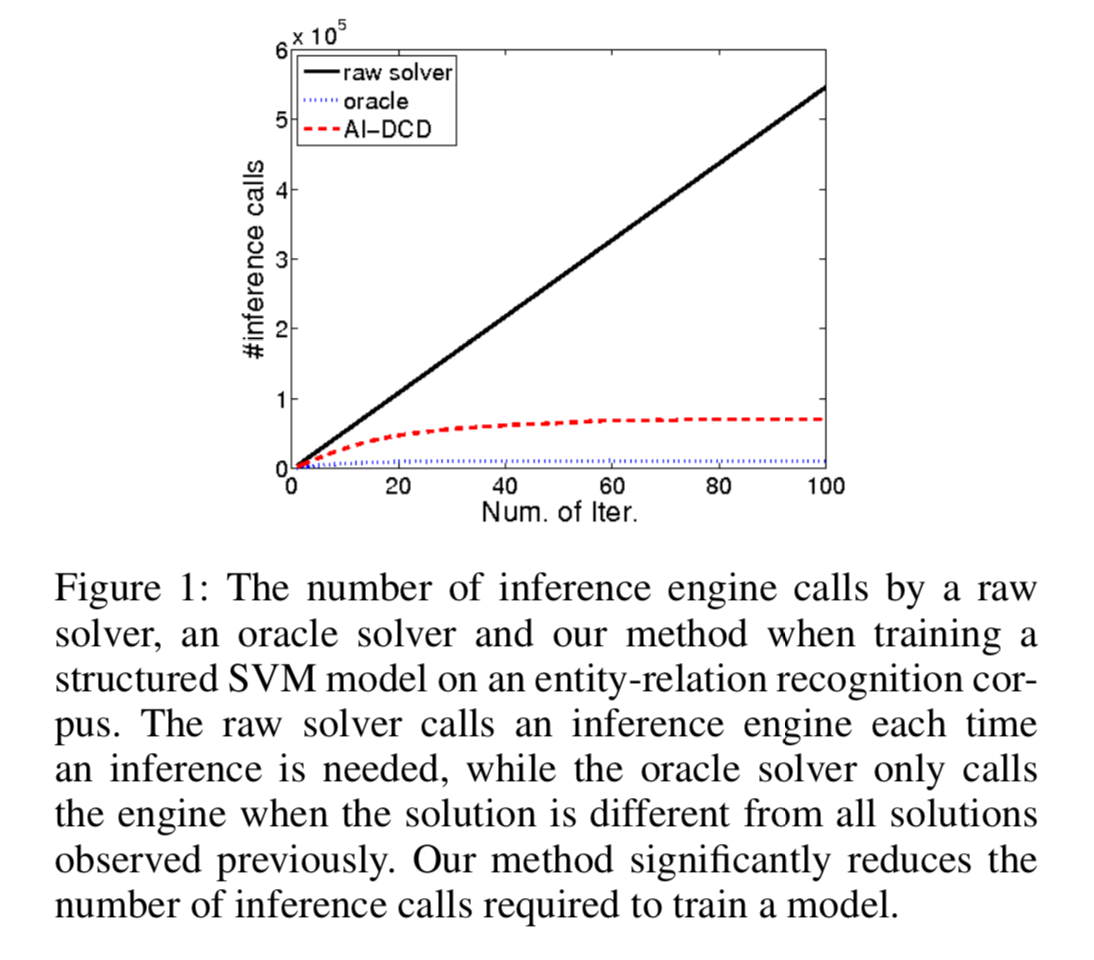
黑线是朴素方法对ILP solver的调用次数,蓝线是理论上所需的最低调用次数(样本的结构数量),红线是平摊推断算法的调用次数。
在提高推断速度的同时,AI-DCD并没有损失精确度:
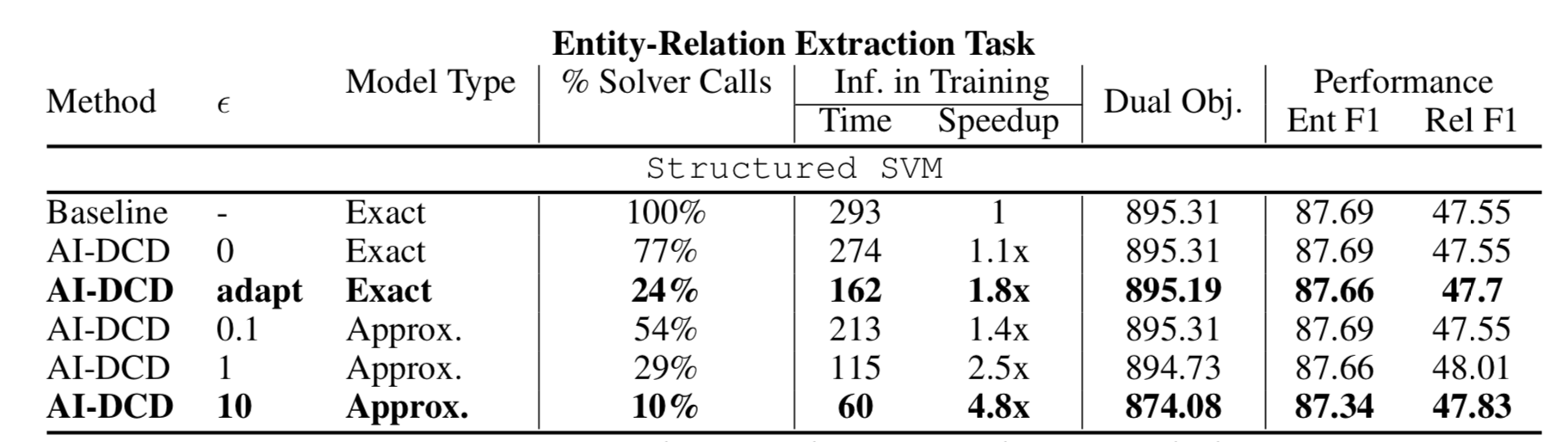
References
[1] K.-W. Chang, S. Upadhyay, G. Kundu, and D. Roth, “Structural Learning with Amortized Inference.,” AAAI, 2015.
http://web.cs.ucla.edu/~kwchang/TAAI17.pdf
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » Structural Learning with Amortized Inference
知识共享署名-非商业性使用-相同方式共享:码农场 » Structural Learning with Amortized Inference
 码农场
码农场