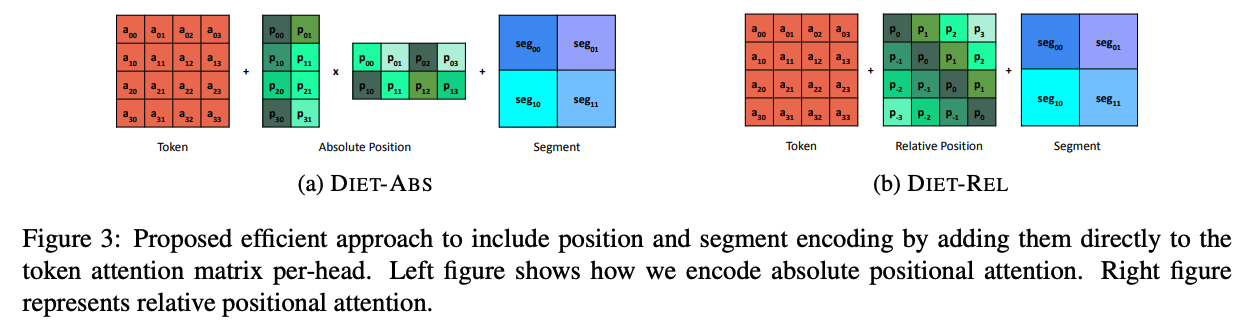
去年流行了一阵相对位置编码,各种巧夺天工的设计层出不穷,各有各的数学解释。然而谷歌这篇文章指出,相对位置并不优于绝对位置。之所以看上去更优是因为位置信息被加到了每一层注意力矩阵上,增大了矩阵的秩。其实我当时看这些论文的时候就很疑惑,这些论文不约而同地把位置特征挪到注意力矩阵上,跟绝对位置编码根本没法直接比较。当时没有深入思考,直到今天看到这篇Google的论文才恍然大悟。
$$\newcommand{\R}{\mathbb{R}} \def\rmA{{\mathbf{A}}} \def\rmB{{\mathbf{B}}} \def\rmC{{\mathbf{C}}} \def\rmD{{\mathbf{D}}} \def\rmE{{\mathbf{E}}} \def\rmF{{\mathbf{F}}} \def\rmG{{\mathbf{G}}} \def\rmH{{\mathbf{H}}} \def\rmI{{\mathbf{I}}} \def\rmJ{{\mathbf{J}}} \def\rmK{{\mathbf{K}}} \def\rmL{{\mathbf{L}}} \def\rmM{{\mathbf{M}}} \def\rmN{{\mathbf{N}}} \def\rmO{{\mathbf{O}}} \def\rmP{{\mathbf{P}}} \def\rmQ{{\mathbf{Q}}} \def\rmR{{\mathbf{R}}} \def\rmS{{\mathbf{S}}} \def\rmT{{\mathbf{T}}} \def\rmU{{\mathbf{U}}} \def\rmV{{\mathbf{V}}} \def\rmW{{\mathbf{W}}} \def\rmX{{\mathbf{X}}} \def\rmY{{\mathbf{Y}}} \def\rmZ{{\mathbf{Z}}} $$
这个结论是可以证明的,设$\rmP \in \R^{n \times d}$为直接相加时输入层的位置嵌入矩阵,而$\hat{\rmP} \in \R^{n \times d_p}$是加到注意力矩阵上的位置矩阵。设$\rmW_Q, \rmW_K \in \R^{d \times d_h}$是query和key的投影矩阵,其中$d_h$为投影大小,并且$d_h < d_p, d$,因为每个注意力头都很小, $n \geq d_h + d_p$因为输入序列一般很长。
那么$\rmA_a = (\rmX+\rmP) \rmW_Q \rmW_K^\top (\rmX+\rmP)^\top$就是加到输入上产生的注意力矩阵(忽略缩放等小细节)了。根据秩的性质,它的秩的上界是受限于每个注意力头的大小的:
$$
\begin{align*}
rank(\rmA_a) &= rank((\rmX+\rmP) \rmW_Q \rmW_K^\top (\rmX+\rmP)^\top) \\
&\le \min(rank(\rmX+\rmP), rank(\rmW_Q), rank(\rmW_K)) \\
&\le d_h.
\end{align*}
$$
因为$rank(\rmW_Q) \leq d_h$是其中秩最小的。
而加到注意力矩阵时产生的新注意力矩阵为$\rmA_r = \rmX \rmW_Q \rmW_K^\top \rmX^\top + \hat{\rmP} \hat{\rmP}^\top $,它的秩可以通过构造法来得到。构造$\rmW_Q = \rmW_K$为前$d_h$行是单位矩阵、其他行为$0$。则两者乘积为:
$$
\rmW_Q \rmW_K^\top = {
\left(
\begin{array}{cc}
I_{d_h, d_h} & 0_{d_h, d-d_h}\\
0_{d-d_h, d_h} & 0_{d-d_h, d-d_h}
\end{array}
\right)
}
$$
构造$\rmX^\top = [I_{d, d} , 0_{n-d, d}]$,则第一项为:
$$
\rmX \rmW_Q \rmW_K^\top \rmX^\top = {
\left(
\begin{array}{cc}
I_{d_h, d_h} & 0_{d_h, n-d_h}\\
0_{n-d_h, d_h} & 0_{n-d_h, n-d_h}
\end{array}
\right) }
$$
构造$\hat{\rmP} = [0_{d,n-d_p}, I_{d_p, d_p}]$,那么:
$$
\hat{\rmP} \hat{\rmP}^\top = {
\left(
\begin{array}{cc}
0_{n-d_p, n-d_p} & 0_{n-d_p, d_p}\\
0_{d_p, n-d_p} & I_{d_p, d_p}
\end{array}
\right)}
$$
两项相加,起作用的只有左上角和右下角的单位矩阵,也就是:
$$
\begin{align*}
rank(\rmA_r) &= rank(\rmX \rmW_Q \rmW_K^\top \rmX^\top + \hat{\rmP} \hat{\rmP}^\top) \\
& = min(d_h + d_p, n) > d_h.
\end{align*}
$$
这个证明虽然不严谨,但得到的下界应该比较宽松(如果你非要构造全$0$矩阵当我没说),实际的权值矩阵很少这么稀疏。
总之,多头注意力机制中的每个头是瓶颈。无论位置编码是相对还是绝对的,先加后过注意力头会被限制秩的大小,而后加则不会。瓶颈是关键,位置编码是次要因素。作者的试验中,绝对位置编码有时候效果甚至更好。
这篇论文还有其他在long Transformer上的应用以及一些分析等,感兴趣的请继续阅读。我从这篇论文中学到的东西是,一些复杂的方法其实是耍花枪,用公式做装饰品。而Google往往能找到问题的本质,一击毙命。
 码农场
码农场