理一理基础优化理论,解释一下深度学习中的一阶梯度下降遇到的病态曲率(pathological curvature)问题。当海森矩阵condition number很大时,一阶梯度下降收敛很慢,无论是对鞍点还是局部极值点而言都不是个好事。
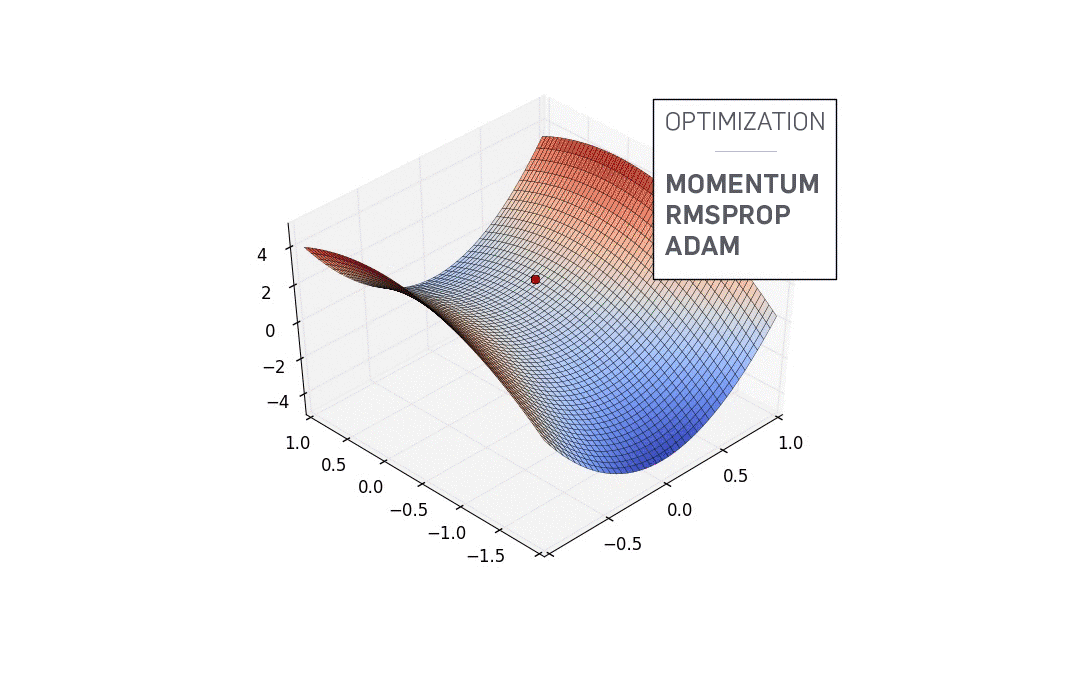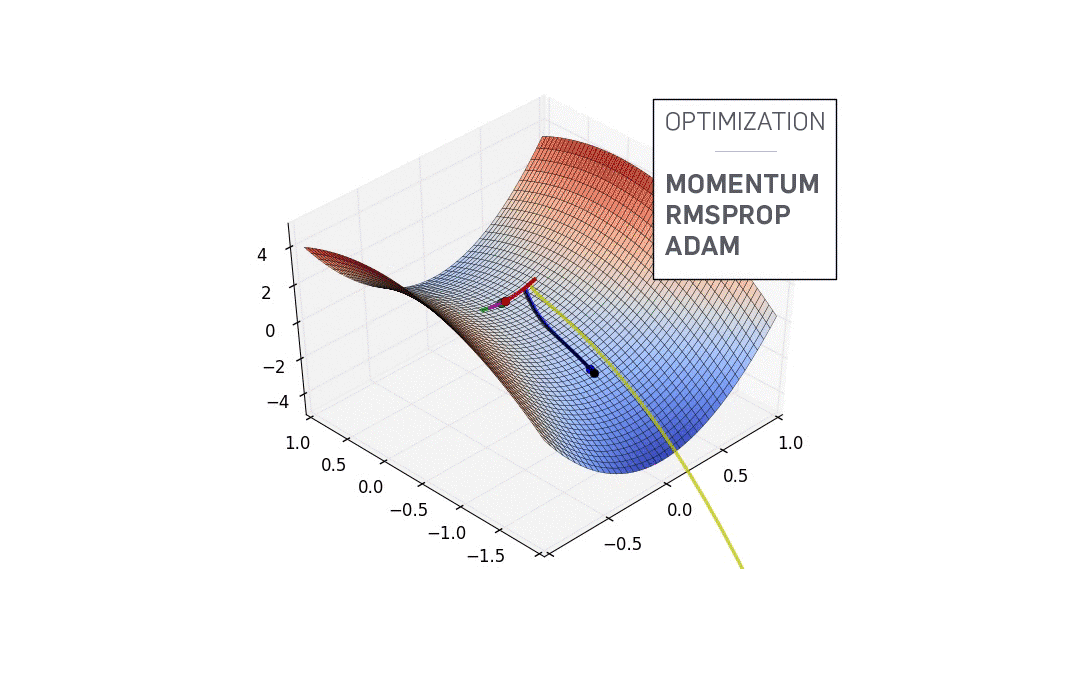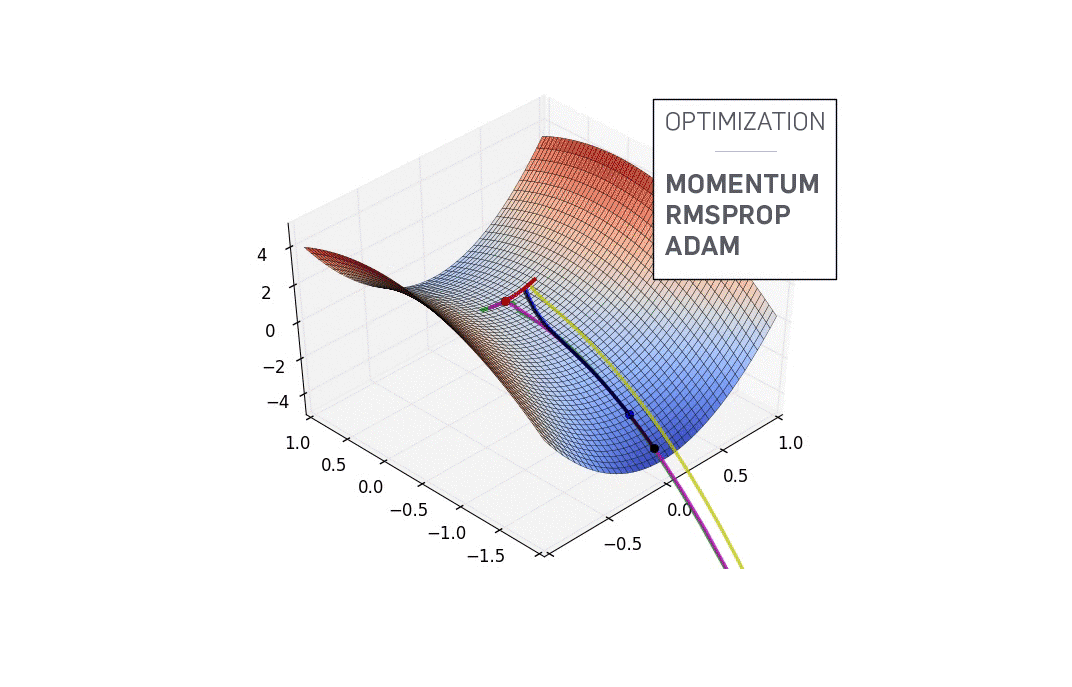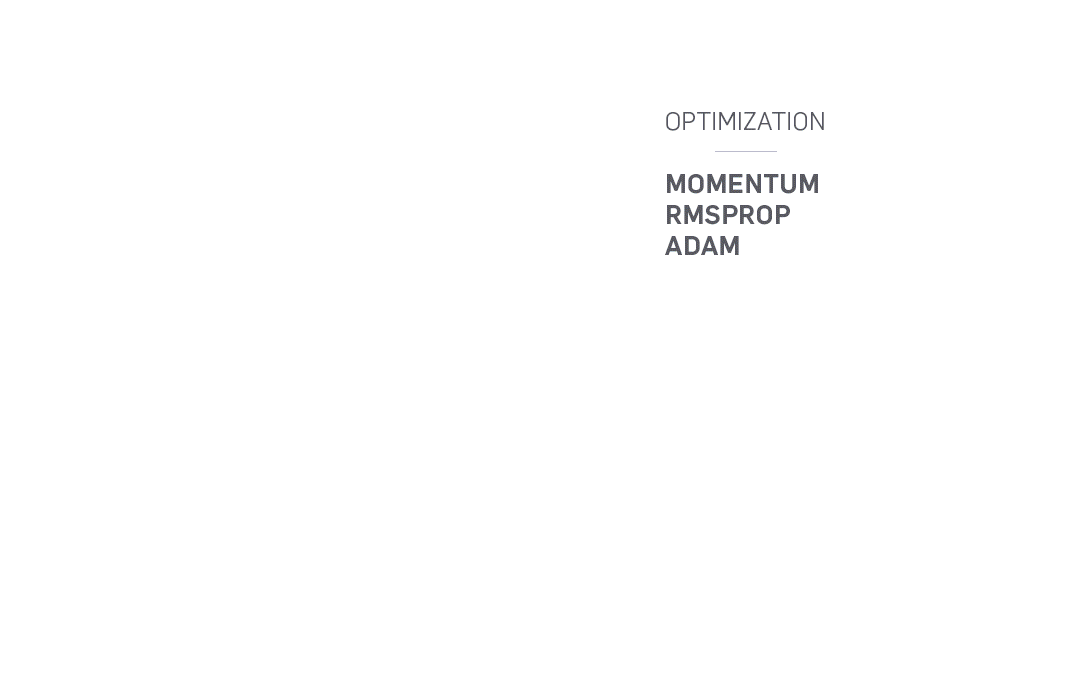
鞍点
$f'(x)=0$时函数不一定抵达局部最优解,还可能是鞍点(见上图),此时还必须根据二阶导数确定。
| $f'(x)$ | $f''(x)$ | $f(x)$ |
|---|---|---|
| $f'(x)=0$ | $f''(x)>0$ | 局部最小值 |
| $f'(x)=0$ | $f''(x)<0$ | 局部最大值 |
| $f'(x)=0$ | $f''(x)=0$ | 局部极值或鞍点 |
对角化
如果一个矩阵$A$可分解为如下乘积:
$$
A = W\Lambda W^{-1}
$$
其中,$W$为可逆矩阵,$\Sigma$是对角矩阵,则$A$是可对角化(diagonalizable)的。$W$的列向量$a_i$是$A$的特征向量,$\Sigma$的主对角线元素为特征向量对应的特征值。亦即:
$$
\begin{align*} W &= {\left(\begin{matrix}a_1 & a_2 & \dots & a_n\end{matrix}\right)} \\ \Lambda &= \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \tag{1} \vdots & \cdots & \ddots & \vdots \\ 0 & \cdots & 0 & \lambda_n \end{bmatrix}\end{align*}
$$
于是,
$$
W\Lambda = {\left(\begin{matrix}\lambda_1 a_1 & \lambda_2 a_2 & \dots & \lambda_n a_n\end{matrix}\right)}
$$
$W$中的$n$个特征向量为标准正交基,即满足$W^TW=I$,等价于$W^T=W^{-1}$,也等价于$W$是Unitary Matrix。
由于对角化定义在方阵上,不适用于一般矩阵。一般矩阵的“对角化”就是大名鼎鼎的奇异值分解了。
奇异值分解
$$
A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V^T_{n\times n}
$$
其中,$AA^T$的特征向量stack为$U$,$A^TA$的特征向量stack为$V$,奇异值矩阵$\Sigma$中对角线元素为$\sigma_i = \frac{Av_i}{u_i} $。
Hessian 矩阵
一阶导数衡量梯度,二阶导数衡量曲率(curvature)。当 $f''(x)<0$, $f(x)$ 往上弯曲;当 $f''(x)>0$时,$f(x)$ 往下弯曲,一个单变量函数的二阶导数如下图所示。
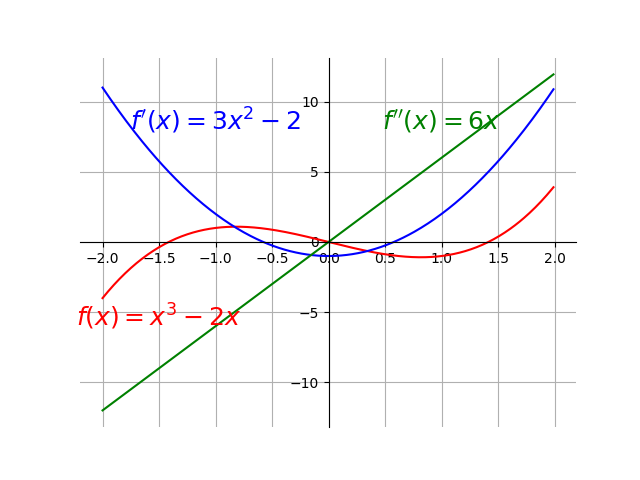
对于多变量函数$f(x, y, z, \dots)$,它的偏导数就是Hessian矩阵:
$$
Hf = \left[ \begin{array}{ccc} \dfrac{\partial^2 f}{\partial \color{blue}{x}^2} & \dfrac{\partial^2 f}{\partial \color{blue}{x} \partial \color{red}{y}} & \dfrac{\partial^2 f}{\partial \color{blue}{x} \partial \color{green}{z}} & \cdots \\\\ \dfrac{\partial^2 f}{\partial \color{red}{y} \partial \color{blue}{x}} & \dfrac{\partial^2 f}{\partial \color{red}{y}^2} & \dfrac{\partial^2 f}{\partial \color{red}{y} \partial \color{green}{z}} & \cdots \\\\ \dfrac{\partial^2 f}{\partial \color{green}{z} \partial \color{blue}{x}} & \dfrac{\partial^2 f}{\partial \color{green}{z} \partial \color{red}{y}} & \dfrac{\partial^2 f}{\partial \color{green}{z}^2} & \cdots \\\\ \vdots & \vdots & \vdots & \ddots \end{array} \right]
$$
$Hf$并不是一个普通的矩阵,而是一个由函数构成的矩阵。也就是说,$\textbf{H}f$的具体取值只有在给定变量值$(x_0, y_0, \dots)$时才能得到。
$$Hf(x_0, y_0, \dots) = \left[ \begin{array}{ccc} \dfrac{\partial^2 f}{\partial \color{blue}{x}^2}(x_0, y_0, \dots) & \dfrac{\partial^2 f}{\partial \color{blue}{x} \partial \color{red}{y}}(x_0, y_0, \dots) & \cdots \\\\ \dfrac{\partial^2 f}{\partial \color{red}{y} \partial \color{blue}{x}}(x_0, y_0, \dots) & \dfrac{\partial^2 f}{\partial \color{red}{y}^2}(x_0, y_0, \dots) & \cdots \\\\ \vdots & \vdots & \ddots \end{array} \right]$$
由于$Hf$是对称的实数矩阵:
$$
\begin{split}& \frac{\delta^2}{\delta x_i \delta x_j} f(x) = \frac{\delta^2}{\delta x_j \delta x_i} f(x) \implies H_{ij} = H_{ji} \\\end{split}
$$
所以它一定是可对角化的。对任意实数对称$n \times n$的矩阵$H$,有如下结论成立:
$$
\forall v \in \mathbb{R^n}, ||v||=1 \implies v^T Hv\leq \lambda_{\max}
$$
证明如下:
由对角化形式$H = Q\Lambda Q^T$得到${\bf v}^TH{\bf v} = {\bf v}^TQ\Lambda Q^T{\bf v}$。定义一个由$\bf{v}$经过$Q^T$转换的向量${\bf y} = Q^T{\bf v}$,于是
$${\bf v}^TH{\bf v} = {\bf y}^T\Lambda {\bf y}\tag{2}$$
将对角矩阵$\Lambda$定义(1)代入有:
$$
\begin{align}{\bf y}^T\Lambda {\bf y}&=\lambda_{\max}y_1^2 + \lambda_{2}y_2^2 + \cdots + \lambda_{\min}y_N^2& \\&\le \lambda_{\max}y_1^2 + \lambda_{\max}y_2^2 + \cdots + \lambda_{\max}y_N^2 \\ & =\lambda_{\max}(y_1^2 +y_2^2 + \cdots y_N^2) \\ & =\lambda_{\max} {\bf y}^T{\bf y} \\ & \implies {\bf y}^T\Lambda {\bf y} \le \lambda_{\max} {\bf y}^T{\bf y} \tag{3}\end{align}
$$
由于$Q^{-1} = Q^T, QQ^T = I$,所以
$$
\begin{eqnarray}{\bf y}^T{\bf y} &= &{\bf v}^TQQ^T{\bf v} = {\bf v}^T{\bf v} \tag{4}\end{eqnarray}
$$
将式(4)代入式(3),有
$$
\begin{eqnarray}{\bf y}^T\Lambda {\bf y} & \le & \lambda_{\max} {\bf y}^T{\bf y} \tag{5}\end{eqnarray}
$$
将式(2)代入式(5),有
$$
{\bf v}^TH{\bf v} \le \lambda_{\max}{\bf v}^T{\bf v}
$$
根据定义${\bf v}^T{\bf v} = \|{\bf v}\|^2$并且$\|{\bf v}\| = 1$,所以
$$
\begin{eqnarray}{\bf v}^TH{\bf v} & \le & \lambda_{\max} \tag{6}\end{eqnarray}
$$
Condition Number of Hessian
任意可对角化矩阵的Condition Number定义如下:
$$\underset{i, j}{\max} \left| \frac{\lambda_i}{\lambda_j} \right|$$
line search
在使用line search确定学习率的梯度下降中,参数点可看做首先往梯度最陡峭方向的垂线方向移动一个步长,接着往次陡峭方向移动一个步长。比如$2$个参数的损失函数:
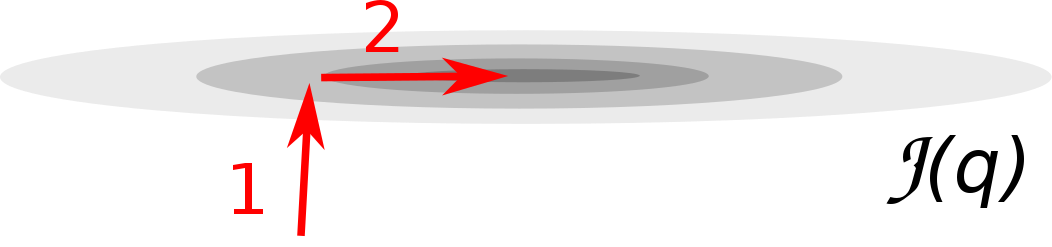
将上面的等高线还原为3d的爬山问题,则如下图所示:

$3$个参数:
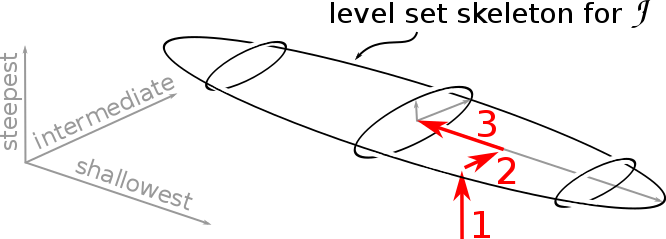
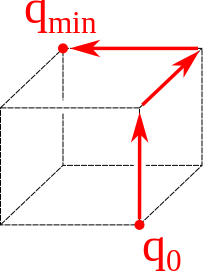
$N$个参数:
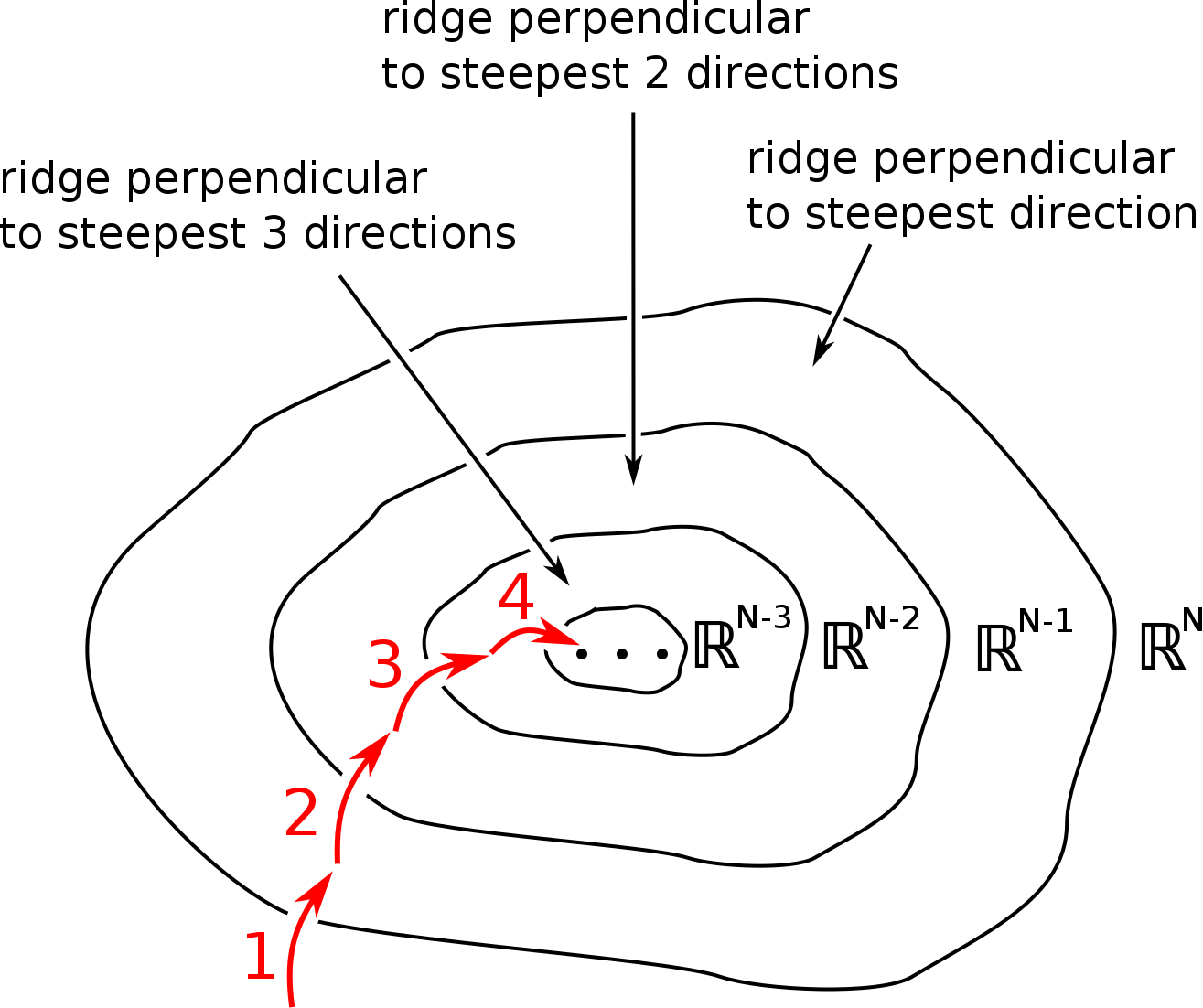
步长(学习率$\epsilon$)是通过如下方式估计的。
根据泰勒级数
$$
\begin{align*}f\left( x \right) & = \sum\limits_{n = 0}^\infty {\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{{\left( {x - a} \right)}^n}} \\ & = f\left( a \right) + f'\left( a \right)\left( {x - a} \right) + \frac{{f''\left( a \right)}}{{2!}}{\left( {x - a} \right)^2} + \frac{{f'''\left( a \right)}}{{3!}}{\left( {x - a} \right)^3} + \cdots \end{align*}
$$
有
$$
\begin{align*}f(x) & = f(x^{(0)}) + (x-x^{(0)})^T g + \frac{1}{2} (x-x^{(0)})^T H (x-x^{(0)}) + \ldots \quad \text{其中 } g \text{ 为偏导数向量} \\f(x) & \approx f(x^{(0)}) + (x-x^{(0)})^T g + \frac{1}{2} (x-x^{(0)})^T H (x-x^{(0)}) \\f(x^{(0)} - \epsilon g) & \approx f(x^{(0)}) - \epsilon g^T g + \frac{1}{2} \epsilon^2 g^T H g \tag{7} \quad\ \text{令} x=x^{(0)} - \epsilon g,\epsilon \in(0,1)\\\end{align*}
$$
这就是梯度下降$x\leftarrow x-\epsilon g$与海森矩阵的联系,$\epsilon$就是学习率。
当$g^T H g\le0$时,$\epsilon$增加会导致$f(x)$减小。但$\epsilon$不能太大,因为$\epsilon $越大泰勒级数中的$\approx$越不准。当$g^T H g>0$时,增大$\epsilon$不一定导致损失函数增加或减小。此时,对式(7)中的$\epsilon$求导,得到最佳学习率为:
$$
\epsilon^{*} = \frac{g^T g}{g^T H g} \geqslant \frac{g^T g}{g^T g \lambda_{max}} = \frac{1}{\lambda_{max}} \quad \text{利用式(7) } g^T H g \leqslant g^T g \lambda_{\max}.\tag{8}
$$
$\lambda_{\max}$是$H$的最大特征值。于是海森矩阵决定了最佳学习率的下界。在使用最佳学习率的情况下,将式(8)代入式(7)有
$$
\begin{split}f(x^{(0)} - \epsilon^{*} g) & \approx f(x^{(0)}) - \frac{1}{2} \epsilon^{*} g^T g \\\end{split}
$$
如果海森矩阵的condition number很差(poor,很大)的话,损失函数在最陡峭的方向的梯度相较于其他方向非常小。如果此时恰好离最优值不远,则非常不幸。
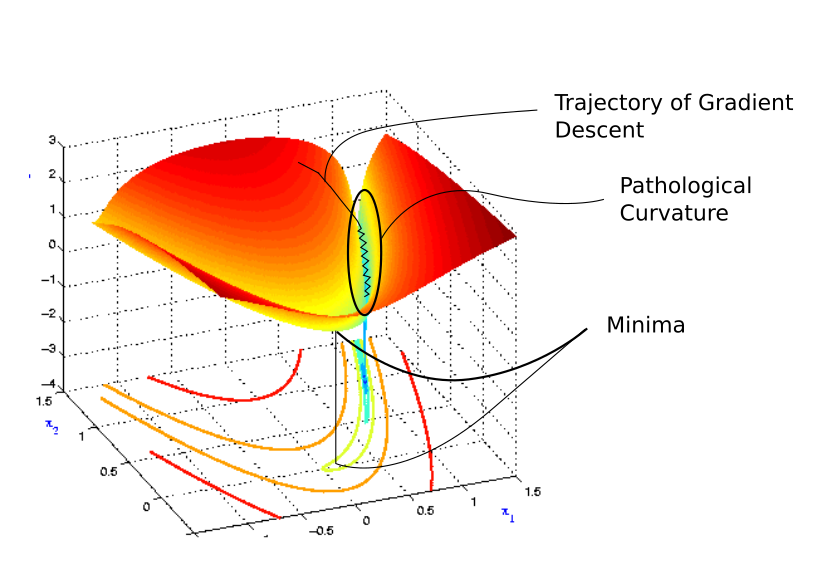
梯度下降要么下降的很慢,要么步长太大跑得太远。
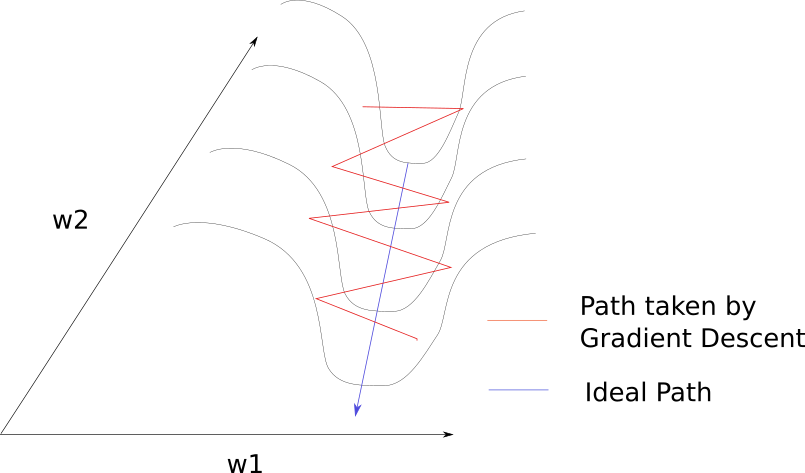
如同在一个狭长的峡谷中一样,梯度下降在两边的峭壁上反复碰撞,很少顺着峡谷往谷底走。
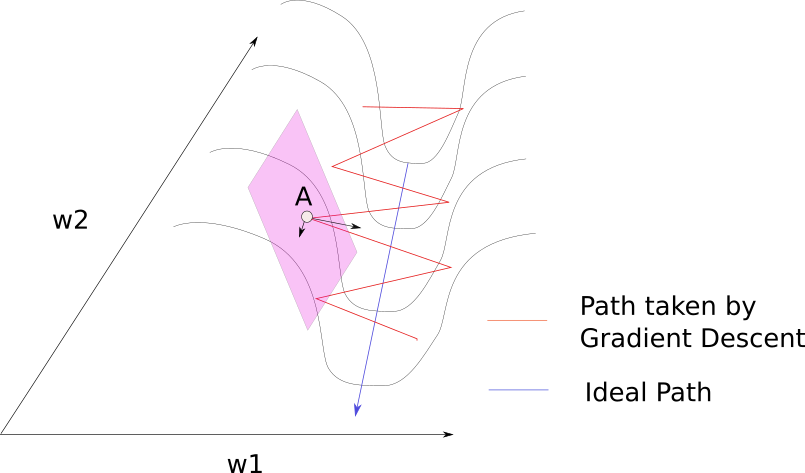
如果有种方法能让参数点在峭壁上采取较小步长,慢慢移动到谷底(而不是一下子撞到对面),然后快速顺流而下就好了。一阶梯度下降只考虑一阶梯度,不知道损失函数的曲率是如何变化的,也就是说不知道下一步会不会离开峭壁。解决方法之一是考虑了二阶梯度的牛顿法。
牛顿法
损失函数的泰勒展开近似,以及相应的导数近似为:
$$
\begin{split}
f(x) & \approx f(x_n) + f'(x_n)\Delta{x} + \frac{1}{2} f''(x_n)\Delta{x}^2 \\
\frac{ df(x)}{d\Delta{x}} & \approx f'(x_n)+ f''(x_n)\Delta{x} \\
\end{split}
$$
令导数为零,找到极值点:
$$
\begin{split}
f'(x_n)+ f''(x_n)\Delta{x} = 0 \\
\Delta{x} = -\frac{f'(x_n)}{f''(x_n)} \\
\end{split}
$$
执行一次迭代:
$$
\begin{split}
x_{n+1} & = x_n + \Delta{x} \\
& = x_n -\frac{f'(x_n)}{f''(x_n)} \\
&=x_{n} -[H f(x_{n})]^{-1} f'(x_{n})\\
\end{split}
$$
写成梯度下降的形式:
$$
\begin{split}
x^{'} = x - [H f(x)]^{-1} f'(x) \\
\end{split}
$$
其中,学习率
$$
\epsilon=[H f(x)]^{-1} f'(x)
$$
学习率与曲率成反比,也就是说在曲率大的方向(垂直于峭壁)的学习率小,而在曲率小的方向(平行于峭壁)的学习率大。也就是是说此时的梯度下降在顺流而下的方向的学习率更大,也就更快收敛了。
 码农场
码农场
最后一个牛顿法的学习率是不是ϵ=[Hf(x)]−1,还要带着导数么
厉害